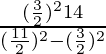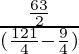Soluciones NCERT Clase 10 – Capítulo 13 Áreas de superficie y volúmenes – Ejercicio 13.3

Pregunta 1. Una esfera metálica de 4,2 cm de radio se funde y se vuelve a moldear en forma de cilindro de 6 cm de radio. Encuentra la altura del cilindro.

Solución:

Radio de esfera (R)= 4,2 cm

Radio del cilindro (r)= 6 cm

En el proceso de refundición, el volumen será el mismo, por lo que

Volumen del cilindro = Volumen de la esfera

πr ² h = $\frac{4}{3}$ πR ³

π(6) ² h = $\frac{4}{3}$ π(4.2) ³ (cancelar π de ambos lados)

36 h = $\frac{4}{3}$ (4,2 × 4,2 × 4,2)

alto = $\frac{4 \times 4.2 \times 4.2 \times 4.2} {3 \times 36}$ (cm)

h = 1,4 × 1,4 × 1,4 (cm)

alto = 2,74 cm

Pregunta 2. Se funden esferas metálicas de radios 6 cm, 8 cm y 10 cm, respectivamente, para formar una sola esfera sólida. Encuentra el radio de la esfera resultante.

Solución:

Radio de la esfera 1 (r ₁ )= 6 cm

Radio de esfera 2 (r ₂ )= 8 cm

Radio de esfera 3 (r ₃ )= 10 cm

Sea Radio de la esfera resultante = R

En el proceso de refundición, el volumen será el mismo, por lo que

Volumen de la esfera resultante = Volumen de la esfera 1 + Volumen de la esfera 2 + Volumen de la esfera 3

$\frac{4}{3}$ π(R) ³ = $\frac{4}{3}$ π(r ₁ ) ³ + $\frac{4}{3}$ π(r ₂ ) ³ + $\frac{4}{3}$ π(r ₃ ) ³ (cancelar $\frac{4}{3}$ π de ambos lados)

R ³ = (r1) ³ + (r2) ³ + (r3) ³

R ³ = (6) ³ + (8) ³ + (10) ³

R3 = 216 ⁺ 512 + 1000

R ³ = 1728

R = (1728) ^1/3

R = 12 cm

Pregunta 3. Se cava un pozo de 20 m de profundidad con un diámetro de 7 m y la tierra de la excavación se extiende uniformemente para formar una plataforma de 22 m por 14 m. Encuentre la altura de la plataforma.

Solución:

Así que básicamente aquí, la excavación de forma cilíndrica se cambia a forma cúbica.

valores dados,

Diámetro del cilindro = 7 m

Radio del cilindro (r)= $\frac{7}{2}$ m

Altura del cilindro (H)= 20 m

Longitud del cuboide (l) = 22 m

Ancho del Cuboide (b) =14 m

Sea Altura del Cuboide = h

En este proceso el volumen será el mismo, por lo que

Volumen de Cuboide = Volumen de Cilindro

l × segundo × h = πr ² H

22 × 14 × h = π × $(\frac{7}{2})^2$ × 20

h = $\frac{\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20}{22 \times 14}$ m (tomando π = $\frac{22}{7}$ )

h = $\frac{5}{2}$ metro

h = 2,5 metros

Pregunta 4. Un pozo de 3 m de diámetro se excava a 14 m de profundidad. La tierra que se ha extraído se ha esparcido uniformemente a su alrededor en forma de anillo circular de 4 m de ancho para formar un terraplén. Encuentre la altura del terraplén.

Solución:

Básicamente, aquí, la excavación de forma cilíndrica se cambia a otra forma cilíndrica hueca.

valores dados,

Diámetro del cilindro = 3 m

Radio del cilindro (r) = $\frac{3}{2}$ m

Altura del cilindro (h) = 14 m

Ancho del terraplén = 4 m

Radio exterior del terraplén R ₁ = radio del cilindro + ancho = 3/2 + 4 = $\frac{11}{2}$ m

Radio interior del terraplén R ₂ = radio del cilindro = $\frac{3}{2}$ m

Altura del terraplén = H

En este proceso el volumen será el mismo, por lo que

Volumen del terraplén = Volumen del cilindro

(πR ₁² H) – (πR ₂² H) = πr ² h

(R ₁² –R ₂² )H = ( $\frac{3}{2}$ ) ² × 14 (cancelar π de ambos lados)

H = $\frac{(\frac{3}{2})^2 × 14}{(\frac{11}{2})^2 - (\frac{3}{2})^2}$

H = $\frac{\frac{63}{2}}{(\frac{121}{4} - \frac{9}{4})}$

H = $\frac{\frac{63}{2}} {\frac{112}{4}}$

H = $\frac{\frac{63}{2}} {28}$

H = $\frac{63}{2×28}$

H = $\frac{9}{8}$ metro

altura = 1,125 m

Pregunta 5. Un recipiente con forma de cilindro circular recto que tiene un diámetro de 12 cm y una altura de 15 cm está lleno de helado. El helado se va a llenar en conos de 12 cm de altura y 6 cm de diámetro, que tienen una forma semiesférica en la parte superior. Encuentre el número de tales conos que se pueden llenar con helado.

Solución:

valores dados,

Radio del cilindro (r) = 6 cm

Altura del cilindro (h) = 15 cm

Radio de cada cono (R) = 3 cm

Altura de cada cono (H) = 12 cm

Sea n el número total de helados

En este proceso el volumen será el mismo, por lo que

n × (Volumen de cada Cono + Volumen de cada hemisferio) = Volumen del Cilindro

norte × ( $\frac{1}{3}$ πR ² H + $\frac{2}{3}$ πR ³ ) = πr ² h

n = $\frac{π(6^2×15)}{π(\frac{1}{3}3^2 ×12 + \frac{2}{3}3^3)}$ (cancelar π de ambos lados)

norte = $\frac{36 \times 15}{\frac{1\times 9 \times12 + 2 \times 27}{3}}$

norte = $\frac{36 \times15}{\frac{162}{3}}$

norte = $\frac{540}{54}$

norte = 10

Por lo tanto, 10 números de conos llenos de helado.

Pregunta 6. ¿Cuántas monedas de plata, de 1,75 cm de diámetro y 2 mm de espesor, se deben fundir para formar un paralelepípedo de dimensiones 5,5 cm × 10 cm × 3,5 cm?

Solución:

valores dados,

Radio de moneda cilíndrica (r) = $\frac{1.75}{2} cm = \frac{175}{200} cm$

Altura de la moneda cilíndrica (H) = 2 mm = $\frac{2}{10}$ cm

Longitud del cuboide (l) = 5,5 cm

Ancho de Cuboide (b) = 10 cm

Altura del Cuboide (h)= 3.5 cm

Sea n el número total de monedas

En este proceso el volumen será el mismo, por lo que

n × (Volumen de cada Moneda) = Volumen del Cilindro

norte × (πR ² H) = l × segundo × h

n × π × ( $\frac{175}{200}$ ) ² × $\frac{2}{10}$ = 5,5 × 10 × 3,5

n = $\frac{\frac{55}{10} × 10 × \frac{35}{10}}{\frac{22}{7} × (\frac{7}{8})^2× \frac{2}{10}}$ (tomando π = $\frac{22}{7}$ )

norte = $\frac{55 \times 10 \times 35 \times 8 \times 8 \times 10 \times 7}{22 \times 7 \times 7 \times 2 \times10 \times 10}$

n = 400

Por lo tanto, se deben derretir 400 monedas de plata para formar este cuboide.

Pregunta 7. Un balde cilíndrico, de 32 cm de alto y con un radio de base de 18 cm, se llena con arena. Este balde se vacía en el suelo y se forma un montón cónico de arena. Si la altura del montón cónico es de 24 cm, encuentre el radio y la altura inclinada del montón.

Solución:

Así que básicamente aquí, la forma cilíndrica se cambia a forma cónica

valores dados,

Radio del cilindro (r) = 18 cm

Altura del cilindro (h) = 32 cm

Altura del cono (H) = 24 cm

Sea Radio del cono = R

En este proceso el volumen será el mismo, por lo que

Volumen del Cono = Volumen del Cilindro

$\frac{1}{3}$ πR ² H = πr ² h

$\frac{1}{3}$ R ² × (24) = 18 ² × 32 (cancele π de ambos lados)

R2 = ^_ $\frac{18 \times 18 \times 32 \times 3}{24}$

R = √(18 × 18 × 4)

R = 36 cm

Altura inclinada (l) = √H ² + R ²

l = √(24 ² + 36 ² )

l = √(12×2) ² + (12×3) ²

l =12 √(4+9)

l = 12 √13 cm

Pregunta 8. El agua en un canal, de 6 m de ancho y 1,5 m de profundidad, fluye con una velocidad de 10 km/h. ¿Cuánta área irrigará en 30 minutos, si se necesitan 8 cm de agua estancada?

Solución:

valores dados,

Ancho del canal (w) = 6 m

Profundidad del canal (h) = 1,5 m

Velocidad del canal = 10 km/hr = (10,000 m/hr)

Para 1 hora (60 minutos) , podemos tomar la longitud (l) como = 10,000 m y

Volumen en 1 hora = (largo × ancho × alto)

= (10.000 × 6 × 1,5) ^m3

= 90.000 m ³

Entonces, durante 30 minutos , el volumen será = $\frac{90000}{30}$ m ³

= 45.000 m ³

El área regada en 30 minutos será como:

Área × longitud de pie = Volumen del canal en 30 minutos

Área = $\frac{45000}{\frac{8}{100}}$

Área = 562500 m ²

Pregunta 9. Un agricultor conecta una tubería de 20 cm de diámetro interno desde un canal a un tanque cilíndrico en su campo, que tiene 10 m de diámetro y 2 m de profundidad. Si el agua fluye por la tubería a razón de 3 km/h, ¿en cuánto tiempo se llenará el tanque?

Solución:

valores dados,

Radio de tubería (R) = 10 cm = $\frac{10}{100}$ m

Radio del tanque cilíndrico (r) = 5 m

Profundidad del tanque cilíndrico (h) = 2 m

Velocidad de los flujos de agua en la tubería = 3 km/hr = (3,000 m/hr)

Sea Tiempo para llenar el tanque cilíndrico = t

Durante 1 hora (60 minutos) , podemos tomar la altura de la tubería (H) como = 3000 m y

Volumen en 1 hora = (πR ² H)

= (π × ( $\frac{1}{10}$ ) ² × 3000) metro ³

= 30π m ³

En este proceso el volumen será el mismo, por lo que

t (en hr) × (Volumen de tubería en 1hr) = Volumen del tanque cilíndrico

t × (30π) = πr ² h

t × (30π) = π × 5 ² × 2

t = $\frac{5 \times 5 \times 2}{30}$

t = $\frac{5}{3}$ hora

t = $\frac{5}{3}$ × 60 minutos

t = 100 minutos

Por lo tanto, se necesitarán 100 minutos para llenar el tanque.

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Una esfera metálica de 4,2 cm de radio se funde y se vuelve a moldear en forma de cilindro de 6 cm de radio. Encuentra la altura del cilindro.

Pregunta 2. Se funden esferas metálicas de radios 6 cm, 8 cm y 10 cm, respectivamente, para formar una sola esfera sólida. Encuentra el radio de la esfera resultante.

Pregunta 3. Se cava un pozo de 20 m de profundidad con un diámetro de 7 m y la tierra de la excavación se extiende uniformemente para formar una plataforma de 22 m por 14 m. Encuentre la altura de la plataforma.

Pregunta 4. Un pozo de 3 m de diámetro se excava a 14 m de profundidad. La tierra que se ha extraído se ha esparcido uniformemente a su alrededor en forma de anillo circular de 4 m de ancho para formar un terraplén. Encuentre la altura del terraplén.

Pregunta 6. ¿Cuántas monedas de plata, de 1,75 cm de diámetro y 2 mm de espesor, se deben fundir para formar un paralelepípedo de dimensiones 5,5 cm × 10 cm × 3,5 cm?

Pregunta 7. Un balde cilíndrico, de 32 cm de alto y con un radio de base de 18 cm, se llena con arena. Este balde se vacía en el suelo y se forma un montón cónico de arena. Si la altura del montón cónico es de 24 cm, encuentre el radio y la altura inclinada del montón.

Pregunta 8. El agua en un canal, de 6 m de ancho y 1,5 m de profundidad, fluye con una velocidad de 10 km/h. ¿Cuánta área irrigará en 30 minutos, si se necesitan 8 cm de agua estancada?

Pregunta 9. Un agricultor conecta una tubería de 20 cm de diámetro interno desde un canal a un tanque cilíndrico en su campo, que tiene 10 m de diámetro y 2 m de profundidad. Si el agua fluye por la tubería a razón de 3 km/h, ¿en cuánto tiempo se llenará el tanque?

Deja una respuesta Cancelar la respuesta