Soluciones NCERT Clase 10 – Capítulo 15 Probabilidad – Ejercicio 15.1 | Serie 1

Teorema 1:

La probabilidad teórica (también llamada probabilidad clásica) de un evento E, escrita como P(E), se define como

P(E) = 

Pregunta 1. Completa las siguientes afirmaciones:

(i) Probabilidad de un evento E + Probabilidad del evento ‘no E’ =_________________ .

(ii) La probabilidad de un evento que no puede suceder es __________. Tal evento se llama __________________.

(iii) La probabilidad de que un evento suceda con certeza es ______________. Tal evento _______________ se llama .

(iv) La suma de las probabilidades de todos los eventos elementales de un experimento es ______________________.

(v) La probabilidad de un evento es mayor o igual a _______________ y ​​menor o _________________ igual a .

Solución:

(yo) 1

(ii) 0, Evento Imposible

(iii) 1, Evento Seguro

(iv) 1

(v) 0, 1

Pregunta 2. ¿Cuál de los siguientes experimentos tiene resultados igualmente probables? Explique.

(i) Un conductor intenta arrancar un automóvil. El coche arranca o no arranca.

(ii) Un jugador intenta tirar una pelota de baloncesto. Dispara o falla el tiro.

(iii) Se hace un ensayo para responder a una pregunta de verdadero o falso. La respuesta es correcta o incorrecta.

(iv) Nace un bebé. Es un niño o una niña.

Solución:

(i) Esta declaración no tiene resultados igualmente probables ya que el automóvil puede arrancar o no dependiendo de varios factores internos y externos como el combustible, la ruta, etc.

(ii) Esta declaración no tiene resultados igualmente probables ya que el jugador puede disparar o fallar el tiro dependiendo de varios factores.

(iii) Esta declaración tiene resultados igualmente probables, ya que se sabe que la solución es correcta o incorrecta, ambas tienen las mismas posibilidades de suceder.

(iv) Esta declaración también tiene resultados igualmente probables, ya que se sabe que el bebé recién nacido puede ser un niño o una niña, ambos tienen las mismas posibilidades de suceder.

Pregunta 3. ¿Por qué se considera que lanzar una moneda al aire es una forma justa de decidir qué equipo debe recibir el balón al comienzo de un partido de fútbol?

Solución:

Tirar una moneda al aire es una forma justa de decidir porque tiene resultados igualmente probables donde el número de resultados posibles es solo 2, es decir , cara o cruz . El lanzamiento se considera completamente imparcial y es impredecible.

Pregunta 4. ¿Cuál de los siguientes no puede ser la probabilidad de un evento?

(A) 2/3

(B) -1.5

(c) 15%

(D) 0,7

Solución:

Como la probabilidad de cualquier evento (E) siempre se encuentra entre 0 y 1 

es decir, 0 ≤ P(E) ≤ 1

(i) 2/3 puede ser la probabilidad de un evento.

(ii) -1.5 no puede ser la probabilidad de un evento.

(iii) 15% puede ser la probabilidad de un evento.

(iv) 0.7 puede ser la probabilidad de un evento.

Pregunta 5. Si P(E) = 0,05, ¿cuál es la probabilidad de ‘no E’?

Solución:

Como, P(E) + P(no E) = 1

⇒ P(No E) = 1 – P(E) (Donde el evento ‘no E’ es complemento del evento E)

Aquí, P(E) = 0,05

Entonces, P(No E) = 1 – 0.05

P(No E) = 0,95

Pregunta 6. Una bolsa contiene únicamente caramelos con sabor a limón. Malini saca un caramelo sin mirar dentro de la bolsa. ¿Cuál es la probabilidad de que saque

(i) un caramelo con sabor a naranja?

(ii) un caramelo con sabor a limón?

Solución:

(i) Como sabemos que la bolsa solo contiene caramelos con sabor a limón.

Por lo tanto, el núm. de caramelos con sabor a naranja = 0

La probabilidad de sacar caramelos con sabor a naranja =   …………………… (del Teorema 1) 

= 0 (Evento Imposible)

(ii) Como solo hay caramelos con sabor a limón, 

P(Caramelos con sabor a limón) = 1 (Evento seguro)

Pregunta 7. Se da que en un grupo de 3 alumnos, la probabilidad de que 2 alumnos no tengan el mismo cumpleaños es 0.992. ¿Cuál es la probabilidad de que los 2 estudiantes tengan el mismo cumpleaños?

Solución:

Como, P(E) + P(no E) = 1

⇒ P(E) = 1 – P(No E) (Donde el evento ‘no E’ es complemento del evento E)

Aquí, P(No E) = Probabilidad de que 2 estudiantes no tengan el mismo cumpleaños = 0.992

Aquí, P(E) = Probabilidad de que los 2 estudiantes tengan el mismo cumpleaños

Entonces, P(E) = 1 – 0.992

P(E) = 0,08

Por lo tanto, la probabilidad de que los 2 estudiantes tengan el mismo cumpleaños es 0.008

Pregunta 8. Una bolsa contiene 3 bolas rojas y 5 bolas negras. Se extrae una bola al azar de la bolsa. ¿Cuál es la probabilidad de que la bola extraída sea 

(yo) rojo? 

(ii) no es rojo?

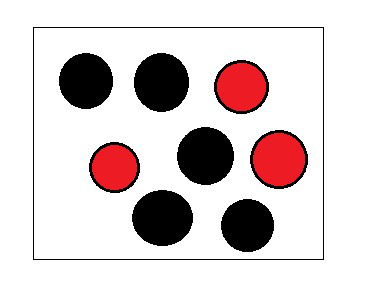
Solución:

Número de bolas rojas = 3

Número de bolas negras = 5

Número total de bolas = 5+3 = 8

Por lo tanto, número total de resultados posibles = 8

(i) P(E) = Probabilidad de que la bola extraída sea roja.

P(E) =   ……………..(Del Teorema 1)

(ii) P(No E) = Probabilidad de que la bola extraída no sea Roja

P(No E) = 1 – P(E) (Donde el evento ‘no E’ es complemento del evento E)

P(No rojo) = 1-  = 

Pregunta 9. Una caja contiene 5 canicas rojas, 8 canicas blancas y 4 canicas verdes. Se saca una canica de la caja al azar. ¿Cuál es la probabilidad de que la canica extraída sea

(yo) rojo? 

(ii) blanco? 

(iii) no es verde?

Solución:

Número de bolas rojas = 5

Número de bolas blancas = 8

Número de bolas verdes = 4

Número total de bolas = 5+8+4 = 17

Por lo tanto, número total de resultados posibles = 17

(i) P(E) = Probabilidad de que la bola extraída sea roja.

P(E) =   …………….. (Del Teorema 1)

(ii) P(E) = Probabilidad de que la bola extraída sea blanca.

P(E) =   …………….. (Del Teorema 1)

(iii) Sea P(E) = Probabilidad de que la bola extraída no sea verde.

P(E) =  ………. (Del Teorema 1)

P(No E) = 1 – P(E) (Donde el evento ‘no E’ es complemento del evento E)

P (no verde) = 1-  = 

Pregunta 10. Una alcancía contiene cien monedas de 50p, cincuenta monedas de ₹ 1, veinte monedas de ₹ 2 y diez monedas de ₹ 5. Si es igualmente probable que una de las monedas se caiga cuando se voltea la banca, ¿cuál es la probabilidad de que la moneda 

(i) será una moneda de 50 p? 

(ii) ¿no será una moneda de ₹ 5?

Solución:

Número de monedas de 50p = 100

Número de monedas de ₹1 = 50

Número de monedas de ₹ 2 = 20

Número de monedas de ₹5 = 10

Número total de monedas = 100+50+20+10 = 180

Por lo tanto, número total de resultados posibles = 180

(i) P(E) = Probabilidad de que la moneda sea una moneda de 50 p.

P(E) =  …………….. (Del Teorema 1)

(ii) Sea P(E) = Probabilidad de que la moneda sea una moneda de ₹5.

P(E) =  . ……………. (Del Teorema 1)

Entonces, P(No E) = Probabilidad de que la moneda no sea de ₹5.

P(No E) = 1 – P(E) (Donde el evento ‘no E’ es complemento del evento E)

P (no moneda de 5 ₹) = 1-

Pregunta 11. Gopi compra un pez en una tienda para su acuario. El comerciante saca un pez al azar de un tanque que contiene 5 peces machos y 8 hembras. ¿Cuál es la probabilidad de que el pez extraído sea un pez macho?

Solución:

Número de peces machos = 5

Número de peces hembra = 8

Número total de peces en el tanque = 5+8 = 13

Por lo tanto, número total de resultados posibles = 13

P(E) = Probabilidad de que el pez sea macho.

P(E) =   ………………. (Del Teorema 1)

Pregunta 12. Un juego de azar consiste en hacer girar una flecha que se detiene apuntando a uno de los números 1, 2, 3, 4, 5, 6, 7, 8 (ver Fig. 15.5), y estos son resultados igualmente probables . ¿Cuál es la probabilidad de que apunte a

(yo) 8?

(ii) un número impar?

(iii) un número mayor que 2?

(iv) un número menor que 9?

Solución:

Aquí, el número total de resultados posibles = 8

(i) P(E) = Probabilidad de que el puntero apunte a 8.

P(E) =   ………………. (Del Teorema 1)

(ii) P(E) = Probabilidad de que la aguja apunte a un número impar.

Número impar = {1,3,5,7}

P(E) =   ………………. (Del Teorema 1)

(iii) P(E) = Probabilidad de que el puntero apunte a un número mayor que 2.

Números mayores que 2 = {3,4,5,6,7,8}

P(E) =   ………………. (Del Teorema 1)

(iv) P(E) = Probabilidad de que el puntero apunte a un número menor que 9.

Números menores que 9 = {1,2,3,4,5,6,7,8}

P(E) =   = 1 ………………. (Del Teorema 1)