Clase 10 Soluciones NCERT – Capítulo 3 Par de ecuaciones lineales en dos variables – Ejercicio 3.5

Pregunta 1. ¿Cuál de los siguientes pares de ecuaciones lineales tiene solución única, ninguna solución o infinitas soluciones? En caso de que haya una solución única, encuéntrela usando el método de multiplicación cruzada.

(i) x – 3y – 3 = 0, 3x – 9y – 2 = 0

Solución:

Aquí,

un ₁ = 1, segundo ₁ = -3, c ₁ = -3

un ₂ = 3, segundo ₂ = -9, c ₂ = -2

Asi que,

$\frac{a_1}{a_2} = \frac{1}{3}$

$\frac{b_1}{b_2} = \frac{-3}{-9} = \frac{1}{3}$

$\frac{c_1}{c_2} = \frac{-3}{-2} = \frac{3}{2}$

Como, $\frac{a_1}{a_2} = \frac{b_1}{b_2} ≠ \frac{c_1}{c_2}$

Por lo tanto, los pares de ecuaciones dados no tienen solución .

(ii) 2x + y = 5, 3x + 2y = 8

Solución:

Reordenando ecuaciones, obtenemos

2x + y -5 = 0

3x + 2y -8 = 0

Aquí,

un ₁ = 2, segundo ₁ = 1, c ₁ = -5

un ₂ = 3, segundo ₂ = 2, c ₂ = -8

Asi que,

$\frac{a_1}{a_2} = \frac{2}{3}$

$\frac{b_1}{b_2} = \frac{1}{2}$

Como, $\frac{a_1}{a_2} ≠ \frac{b_1}{b_2}$

Por lo tanto, los pares de ecuaciones dados tienen solución única .

Para la multiplicación cruzada,

$\mathbf{\frac{x}{b_1c_2-b_2c_1} = \frac{y}{c_1a_2-c_2a_1} = \frac{1}{a_1b_2-a_2b_1}}$

$\frac{x}{(1)(-8)-(2)(-5)} = \frac{y}{(-5)(3)-(-8)(2)} = \frac{1}{(2)(2)-(3)(1)}$

$\frac{x}{(-8)+10} = \frac{y}{(-15)+16} = \frac{1}{4-3}$

$\frac{x}{2}$ = y = 1

Por eso,

$\frac{x}{2}$ = 1

x = 2

y, y = 1

Por lo tanto, la solución requerida es x = 2 e y = 1 .

(iii) 3x – 5y = 20, 6x – 10y = 40

Solución:

Reordenando ecuaciones, obtenemos

3x – 5y – 20 = 0

6x – 10y – 40 = 0

Aquí,

a1 = 3, b1 = _-5 , c1 = -20

a ₂ = 6, b ₂ = -10, c ₂ = -40

Asi que,

$\frac{a_1}{a_2} = \frac{3}{6} = \frac{1}{2}$

$\frac{b_1}{b_2} = \frac{-5}{-10} = \frac{1}{2}$

$\frac{c_1}{c_2} = \frac{-20}{-40} = \frac{1}{2}$

Como,

$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$

Por lo tanto, los pares de ecuaciones dados tienen infinitas soluciones .

(iv) x – 3y – 7 = 0, 3x – 3y – 15 = 0

Solución:

Aquí,

a1 = 1, b1 = -3, c1 = _-7

a ₂ = 3, b ₂ = -3, c ₂ = -15

Asi que,

$\frac{a_1}{a_2} = \frac{1}{3}$

$\frac{b_1}{b_2} = \frac{-3}{-3} = 1$

Como,

$\frac{a_1}{a_2} ≠ \frac{b_1}{b_2}$

Por lo tanto, los pares de ecuaciones dados tienen solución única .

Para la multiplicación cruzada,

$\mathbf{\frac{x}{b_1c_2-b_2c_1} = \frac{y}{c_1a_2-c_2a_1} = \frac{1}{a_1b_2-a_2b_1}}$

$\frac{x}{(-3)(-15)-(-3)(-7)} = \frac{y}{(-7)(3)-(-15)(1)} = \frac{1}{(1)(-3)-(3)(-3)}$

$\frac{x}{45-21} = \frac{y}{(-21)+15} = \frac{1}{-3+9}$

$\frac{x}{24} = \frac{y}{-6} = \frac{1}{6}$

Por eso,

x = $\frac{24}{6}$

x = 4

y, y = $\frac{-6}{6}$

y = -1

Por lo tanto, la solución requerida es x = 4 e y = -1 .

Pregunta 2. (i) ¿Para qué valores de a y b tiene el siguiente par de ecuaciones lineales un número infinito de soluciones?

2x + 3y = 7

(a – b) x + (a + b) y = 3a + b – 2

Solución:

Aquí,

a ₁ = 2, b1 = 3, c1 = -7

a ₂ = ab, b ₂ = a+b, c ₂ = -(3a+b-2)

Para tener un número infinito de soluciones, tiene que satisfacer las siguientes condiciones:

$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$

$\frac{2}{a-b} = \frac{3}{a+b} = \frac{7}{(3a+b-2)}$

Ahora bien, al comparar

$\frac{2}{a-b} = \frac{3}{a+b}$

2(a+b) = 3(ab)

2a+2b = 3a – 3b

a – 5b = 0 …………………(1)

Y ahora comparando

$\frac{3}{a+b} = \frac{7}{(3a+b-2)}$

3(3a+b-2) = 7(a+b)

9a+3b-6 = 7a+7b

2a-4b-6=0

Reduciendo la forma, obtenemos

a-2b-3=0 …………………(2)

Ahora, nuevos valores para

un ₁ = 1, segundo ₁ = -5, c ₁ = 0

un ₂ = 1, segundo ₂ = -2, c ₂ = -3

Resolviendo Eq(1) y Eq(2), por multiplicación cruzada,

$\mathbf{\frac{a}{b_1c_2-b_2c_1} = \frac{b}{c_1a_2-c_2a_1} = \frac{1}{a_1b_2-a_2b_1}}$

$\frac{a}{(-5)(-3)-(-2)(0)} = \frac{b}{(0)(1)-(-3)(1)} = \frac{1}{(1)(-2)-(1)(-5)}$

$\frac{a}{15-0} = \frac{b}{0+3} = \frac{1}{-2+5}$

$\frac{a}{15} = \frac{b}{3} = \frac{1}{3}$

Por eso,

un = $\frac{15}{3}$

un = 5

y, b = $\frac{3}{3}$

segundo = 1

Por lo tanto, Para valores a = 5 y b = 1 par de ecuaciones lineales tienen un número infinito de soluciones

(ii) ¿Para qué valor de k el siguiente par de ecuaciones lineales no tendrá solución?

3x + y = 1

(2k – 1) x + (k – 1) y = 2k + 1

Solución:

Aquí,

un ₁ = 3, segundo ₁ = 1, c ₁ = -1

a ₂ = (2k-1), b ₂ = k-1, c ₂ = -(2k+1)

Para no tener solución, tiene que satisfacer las siguientes condiciones:

$\frac{a_1}{a_2} = \frac{b_1}{b_2} ≠ \frac{c_1}{c_2}$

$\frac{3}{2k-1} = \frac{1}{k-1} ≠ \frac{1}{2k+1}$

Ahora bien, al comparar

$\frac{3}{2k-1} = \frac{1}{k-1}$

3(k-1) = 2k-1

3k-3 = 2k-1

k = 2

Y ahora comparando

$\frac{1}{k-1} ≠ \frac{1}{2k+1}$

2k+1 ≠ k-1

k ≠ -2

Por lo tanto, para k = 2 y k ≠ -2 el par de ecuaciones lineales no tiene solución .

Pregunta 3. Resuelva el siguiente par de ecuaciones lineales por los métodos de sustitución y multiplicación cruzada:

8x + 5y = 9

3x + 2y = 4

Solución:

8x + 5y – 9 = 0 …………………(1)

3x + 2y – 4 = 0 …………………(2)

Método de sustitución

De la ecuación (2), obtenemos

x = 4-2y/3

Ahora, sustituyéndolo en la ecuación (1), obtenemos

8(4-2y/3) + 5y – 9 = 0

32-16 años/3 + 5 años – 9 = 0

32 – 16 años + 15 años – 27 = 0

y = 5

Ahora, sustituyendo y = 5 en la ecuación (2), obtenemos

3x + 2(5) – 4 = 0

3x = -6

x = -2

Método de multiplicación cruzada

Aquí,

un ₁ = 8, segundo ₁ = 5, c ₁ = -9

un ₂ = 3, segundo ₂ = 2, c ₂ = -4

Asi que,

$\frac{a_1}{a_2} = \frac{8}{3}$

$\frac{b_1}{b_2} = \frac{5}{2}$

Como,

$\frac{a_1}{a_2} ≠ \frac{b_1}{b_2}$

Por lo tanto, los pares de ecuaciones dados tienen solución única.

Para la multiplicación cruzada,

$\mathbf{\frac{x}{b_1c_2-b_2c_1} = \frac{y}{c_1a_2-c_2a_1} = \frac{1}{a_1b_2-a_2b_1}}$

$\frac{x}{(5)(-4)-(2)(-9)} = \frac{y}{(-9)(3)-(-4)(8)} = \frac{1}{(8)(2)-(3)(5)}$

$\frac{x}{(-20)+18} = \frac{y}{(-27)+32} = \frac{1}{16-15}$

$\frac{x}{-2} = \frac{y}{5}$ = 1

Por eso,

$\frac{x}{-2}$ = 1

x = -2

y, $\frac{y}{-5}$ = 1

y = 5

Por lo tanto, la solución requerida es x = -2 e y = 5 .

Pregunta 4. Forme el par de ecuaciones lineales en los siguientes problemas y encuentre sus soluciones (si existen) por cualquier método algebraico:

(i) Una parte de los cargos mensuales del albergue es fija y el resto depende de la cantidad de días que se haya tomado alimentos en el comedor. Cuando un estudiante A toma comida para 20 días, tiene que pagar ₹ 1000 como cargos de albergue, mientras que un estudiante B, que toma comida para 26 días, paga ₹ 1180 como cargos de albergue. Encuentre los cargos fijos y el costo de los alimentos por día.

Solución:

Echemos,

Cargo fijo = x

Cargo de alimentos por día = y

De acuerdo con la pregunta dada,

x + 20y = 1000 ……………….. (1)

x + 26y = 1180 ………………..(2)

Restando Eq(1) de Eq(2) obtenemos

6 años = 180

y = 30

Ahora, sustituyendo y = 30 en la ecuación (2), obtenemos

x + 20(30) = 1000

x = 1000 – 600

x = 400.

Por lo tanto, los cargos fijos son ₹ 400 y el cargo por día es ₹ 30 .

(ii) Una fracción se convierte 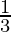$\frac{1}{3}$ cuando se resta 1 al numerador, y se convierte 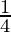$\frac{1}{4}$ cuando se suma 8 a su denominador. Encuentra la fracción.

Solución:

Sea la fracción $\frac{x}{y}$ .

Entonces, según la pregunta dada,

$\frac{x-1}{y} = \frac{1}{3}$

3x – y = 3 …………………(1)

$\frac{x}{y+8} = \frac{1}{4}$

4x –y =8 ………………..(2)

Restando Eq(1) de Eq(2), obtenemos

x = 5

Ahora, sustituyendo x = 5 en la ecuación (2), obtenemos

4(5)– y = 8

y = 12

Por lo tanto, la fracción es $\mathbf{\frac{5}{12}}$ .

(iii) Yash obtuvo 40 puntos en una prueba, obtuvo 3 puntos por cada respuesta correcta y perdió 1 punto por cada respuesta incorrecta. Si se hubieran otorgado 4 puntos por cada respuesta correcta y se hubieran deducido 2 puntos por cada respuesta incorrecta, Yash habría obtenido 50 puntos. ¿Cuántas preguntas había en la prueba?

Solución:

Echemos

Número de respuestas correctas = x

Número de respuestas incorrectas = y

De acuerdo con la pregunta dada;

3x−y=40 ……….……..(1)

4x−2y=50

2x−y=25 ……………….(2)

Restando la ecuación (2) de la ecuación (1), obtenemos

X = 15

Ahora, sustituyendo x = 15 en la ecuación (2), obtenemos

2(15) – y = 25

y = 30-25

y = 5

Por lo tanto, número de respuestas correctas = 15 y número de respuestas incorrectas = 5

Por lo tanto, número total de preguntas = 20

(iv) Los lugares A y B están separados por 100 km en una carretera. Un automóvil parte de A y otro de B al mismo tiempo. Si los autos viajan en la misma dirección a diferentes velocidades, se encuentran en 5 horas. Si viajan el uno hacia el otro, se encuentran en 1 hora. ¿Cuáles son las velocidades de los dos autos?

Solución:

Echemos

Velocidad del coche desde el punto A = x km/he

Velocidad del coche desde el punto B = y km/h

Cuando el automóvil viaja en la misma dirección,

5x – 5y = 100

x – y = 20 ………………(1)

Cuando el automóvil viaja en la dirección opuesta,

x + y = 100 ………………..(2)

Restando la ecuación (1) de la ecuación (2), obtenemos

2 años = 80

y = 40

Ahora, sustituyendo y = 40 en la ecuación (1), obtenemos

x-40 = 20

x = 60

Por lo tanto, la velocidad del automóvil desde el punto A = 60 km/h

Velocidad del automóvil desde el punto B = 40 km/h.

(v) El área de un rectángulo se reduce en 9 unidades cuadradas si su largo se reduce en 5 unidades y el ancho aumenta en 3 unidades. Si aumentamos el largo en 3 unidades y el ancho en 2 unidades, el área aumenta en 67 unidades cuadradas. Encuentra las dimensiones del rectangulo.

Solución:

Echemos

Longitud del rectángulo = x unidad

Ancho del rectángulo = y unidad

El área del rectángulo será = xy unidades cuadradas

Según las condiciones dadas,

(x – 5) (y + 3) = xy -9

3x – 5y – 6 = 0 ……………………(1)

(x + 3) (y + 2) = xy + 67

2x + 3y – 61 = 0 ……………………..(2)

Usando el método de multiplicación cruzada, obtenemos,

$\frac{x}{(-5)(-61)-(3)(-6)} = \frac{y}{(-6)(2)-(-61)(3)} = \frac{1}{(3)(3)-(2)(-5)}$

$\frac{x}{305 +18} = \frac{y}{-12+183} = \frac{1}{9+10}$

$\frac{x}{323} = \frac{y}{171} = \frac{1}{19}$

Por eso,

$\frac{x}{323} = \frac{1}{19}$

x = 17

y, $\frac{y}{171} = \frac{1}{19}$

y = 9

Por lo tanto, la solución requerida es x = 17 e y = 9.

Longitud del rectángulo = 17 unidades

Ancho del rectángulo = 9 unidades

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. ¿Cuál de los siguientes pares de ecuaciones lineales tiene solución única, ninguna solución o infinitas soluciones? En caso de que haya una solución única, encuéntrela usando el método de multiplicación cruzada.

(i) x – 3y – 3 = 0, 3x – 9y – 2 = 0

(ii) 2x + y = 5, 3x + 2y = 8

(iii) 3x – 5y = 20, 6x – 10y = 40

(iv) x – 3y – 7 = 0, 3x – 3y – 15 = 0

Pregunta 2. (i) ¿Para qué valores de a y b tiene el siguiente par de ecuaciones lineales un número infinito de soluciones?

2x + 3y = 7

(a – b) x + (a + b) y = 3a + b – 2

(ii) ¿Para qué valor de k el siguiente par de ecuaciones lineales no tendrá solución?

3x + y = 1

(2k – 1) x + (k – 1) y = 2k + 1

Pregunta 3. Resuelva el siguiente par de ecuaciones lineales por los métodos de sustitución y multiplicación cruzada:

8x + 5y = 9

3x + 2y = 4

Pregunta 4. Forme el par de ecuaciones lineales en los siguientes problemas y encuentre sus soluciones (si existen) por cualquier método algebraico:

(ii) Una fracción se convierte cuando se resta 1 al numerador, y se convierte cuando se suma 8 a su denominador. Encuentra la fracción.

(v) El área de un rectángulo se reduce en 9 unidades cuadradas si su largo se reduce en 5 unidades y el ancho aumenta en 3 unidades. Si aumentamos el largo en 3 unidades y el ancho en 2 unidades, el área aumenta en 67 unidades cuadradas. Encuentra las dimensiones del rectangulo.

Deja una respuesta Cancelar la respuesta

(ii) Una fracción se convierte $\frac{1}{3}$ cuando se resta 1 al numerador, y se convierte $\frac{1}{4}$ cuando se suma 8 a su denominador. Encuentra la fracción.