Clase 10 Soluciones NCERT – Capítulo 3 Par de ecuaciones lineales en dos variables – Ejercicio 3.6

Pregunta 1. Resuelve los siguientes pares de ecuaciones reduciéndolas a un par de ecuaciones lineales:

(i) 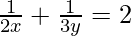$\frac{1}{2x} + \frac{1}{3y} = 2$

$\frac{1}{3x} + \frac{1}{2y}= \frac{13}{6}$

Solución:

Tomemos 1/x = a y 1/y = b

Aquí, las dos ecuaciones dadas serán las siguientes:

$\frac{a}{2}$ + $\frac{b}{3}$ = 2

Multiplícalo por 6, obtenemos

3a + 2b = 12 -(1)

y,

$\frac{a}{3}$ + $\frac{b}{2}$ = $\frac{13}{6}$

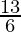
Multiplícalo por 6, obtenemos

2a + 3b = 13 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(1) por 2 y multiplique eq(2) por 3, y luego réstelos

5b = 15

segundo = 3

Ahora poniendo b = 3 en la ecuación (1), obtenemos

3a + 2(3) = 12

a = 6/3

un = 2

Entonces, ahora como

a = 1/x = 2

X = 1/2

b = 1/y = 3

y = 1/3

(ii) 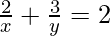$\frac{2}{√x} + \frac{3}{√y} = 2$

$\frac{4}{√x} - \frac{9}{√y} = -1$

Solución:

Tomemos 2/√x = a y 3/√y = b

Aquí, las dos ecuaciones dadas serán las siguientes:

a + b = 2 -(1)

y,

2a – 3b =-1 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(1) por 3, y luego súmelos

5a = 5

un = 1

Ahora poniendo a = 1 en la ecuación (1), obtenemos

1 + b = 2

segundo = 1

Entonces, ahora como

a = 2/√x = 1

√x = 2

x = 4

b = 3/√y = 1

√x = 3

y = 9

(iii) 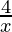$\frac{4}{x}$ + 3y = 14

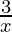$\frac{3}{x}$ – 4 años = 23

Solución:

Vamos, tomemos 1/x = a

Aquí, las dos ecuaciones dadas serán las siguientes:

4a + 3y = 14 -(1)

y,

3a – 4y = 23 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(1) por 3 y multiplique eq(2) por 4, y luego réstelos

-25 años = 50

y = -2

Ahora poniendo y = -2 en la ecuación (1), obtenemos

4a + 3(-2) = 14

4a = 20

un = 5

Entonces, ahora como

a = 1/x = 5

X = 1/5

y = -2

(iv) 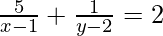$\frac{5}{x-1} + \frac{1}{y-2} = 2$

$\frac{6}{x-1} - \frac{3}{y-2} = 1$

Solución:

Vamos, tomemos $\frac{1}{x-1}$ = a y, $\frac{1}{y-2}$ = b

Aquí, las dos ecuaciones dadas serán las siguientes:

5a + b = 2 -(1)

y,

6a – 3b = 1 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(1) por 3, y luego súmelos

21a = 7

un = 1/3

Ahora poniendo a = 1/3 en la ecuación (1), obtenemos

5(1/3) + b = 2

b = 2 – 5/3

b = 1/3

Entonces, ahora como

un = $\frac{1}{x-1} = \frac{1}{3}$

x-1 = 3

x = 4

segundo = $\frac{1}{y-2} = \frac{1}{3}$

y-2 = 3

y = 5

(v) $\frac{7x-2y}{xy} = 5$

$\frac{8x+7y}{xy}=15$

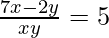
Solución:

$\frac{7}{y} - \frac{2}{x}$ = 5

$\frac{8}{y} + \frac{7}{x}$ = 15

Tomemos 1/x = a y 1/y = b

Aquí, las dos ecuaciones dadas serán las siguientes:

7b – 2a = 5 -(1)

y,

8b + 7a = 15 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(1) por 7, multiplique eq(2) por 2 y luego súmelos

65b = 65

segundo = 1

Ahora poniendo b = 1 en eq(1), obtenemos

7(1) – 2a = 5

2a = 7 – 5

un = 1

Entonces, ahora como

a = 1/x = 1

X = 1

b = 1/y = 1

y = 1

(vi) 6x + 3y = 6xy

2x + 4y = 5xy

Solución:

Dividiendo ambas ecuaciones por xy, obtenemos

$\frac{6}{y} + \frac{3}{x}$ = 6

$\frac{2}{y} + \frac{4}{x}$ = 5

Tomemos 1/x = a y 1/y = b

Aquí, las dos ecuaciones dadas serán las siguientes:

6b + 3a = 6

Divide la ecuación anterior por 2,

2b + a = 2 -(1)

y,

2b + 4a = 5 -(2)

Ahora, usando el método de eliminación,

Restar eq(1) de eq(2), obtenemos

3a = 3

un = 1

Ahora poniendo a = 1 en la ecuación (1), obtenemos

2b + 1 = 2

segundo = 1/2

Entonces, ahora como

a = 1/x = 1

X = 1

b = 1/y = 1/2

y = 2

(vii) 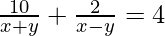$\frac{10}{x+y} + \frac{2}{x-y}=4$

$\frac{15}{x+y} - \frac{5}{x-y}=-2$

Solución:

Vamos, tomemos $\frac{1}{x+y}$ = a y $\frac{1}{x-y}$ = b

Aquí, las dos ecuaciones dadas serán las siguientes:

10a + 2b = 4

Divide la ecuación anterior por 2,

5a + b = 2 -(1)

y,

15a – 5b = -2 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(1) por 3 y réstelos,

8b = 8

segundo = 1

Ahora poniendo b = 1 en eq(1), obtenemos

5a + 1 = 2

a = 1/5

Entonces, ahora como

un = $\frac{1}{x+y}$ = $\frac{1}{5}$

x + y = 5 -(3)

segundo = $\frac{1}{x-y}$ = 1

x – y = 1 -(4)

Sumando las ecuaciones (3) y (4), obtenemos

2x = 6

x = 3 y y = 2

(viii) $\frac{1}{3x+y} + \frac{1}{3x-y}= \frac{3}{4}$

$\frac{1}{2(3x+y)} - \frac{1}{2(3x-y)} = \frac{-1}{8}$

Solución:

Vamos, toma $\frac{1}{3x+y}$ = a

y, $\frac{1}{3x-y}$ = b

Aquí, las dos ecuaciones dadas serán las siguientes:

a + b = 3/4 -(1)

y,

$\frac{a}{2} - \frac{b}{2} = \frac{-1}{8}$

Multiplícalo por 2, obtenemos

a – b = -1/4 -(2)

Ahora, usando el método de eliminación,

Suma eq(1) y eq(1), obtenemos

2a = 1/2

un = 1/4

Ahora poniendo a = 1/4 en la ecuación (1), obtenemos

$\frac{1}{4}$ + b = $\frac{3}{4}$

segundo = 1/2

Entonces, ahora como

un = $\frac{1}{3x+y} = \frac{1}{4}$

3x + y = 4 -(3)

segundo = $\frac{1}{3x-y} = \frac{1}{2}$

3x – y = 2 -(4)

Sumando eq(3) y eq(4), obtenemos

6x = 6

x = 1 y y = 1

Pregunta 2. Formule los siguientes problemas como un par de ecuaciones y, por lo tanto, encuentre sus soluciones:

(i) Ritu puede remar río abajo 20 km en 2 horas y río arriba 4 km en 2 horas. Encuentre su velocidad de remar en aguas tranquilas y la velocidad de la corriente.

Solución:

Dejenos considerar,

Velocidad de Ritu en aguas tranquilas = x km/hr

Velocidad de la corriente = y km/h

Ahora, la velocidad de Ritu durante,

Aguas abajo = (x + y) km/h

Aguas arriba = (x – y) km/h

como velocidad = $\frac{Distance}{Time}$

De acuerdo con la pregunta dada,

x + y = 20/2

x + y = 10 -(1)

y,

x – y = 4/2

x – y = 2 -(2)

Suma eq(1) y eq(2), obtenemos

2x = 12

x = 6 y y = 4

Por lo tanto, la velocidad de Ritu remando en aguas tranquilas = 6 km/h

Velocidad de la corriente = 4 km/h

(ii) 2 mujeres y 5 hombres juntos pueden terminar un trabajo de bordado en 4 días, mientras que 3 mujeres y 6 hombres pueden terminarlo en 3 días. Encuentre el tiempo que tarda 1 mujer sola en terminar el trabajo, y también el que tarda 1 hombre solo.

Solución:

Echemos,

El número total de días que tardan las mujeres en terminar el trabajo = x

El número total de días que tardan los hombres en terminar el trabajo = y

El trabajo realizado por las mujeres en un día será = 1/x

El trabajo realizado por las mujeres en un día será = 1/y

Entonces, de acuerdo con la pregunta

4( $\frac{2}{x} + \frac{5}{y}$ ) = 1

Y, 3( $\frac{3}{x} + \frac{6}{y}$ ) = 1

Tomemos 1/x = a y 1/y = b

Aquí, las dos ecuaciones dadas serán las siguientes:

4(2a + 5b) = 1

8a + 20b = 1 -(1)

y,

3(3a + 6b) = 1

9a + 18b = 1 -(2)

Ahora, usando el método de multiplicación cruzada,

$\frac{a}{20-18} = \frac{b}{9-8} = \frac{1}{180-144}$

$\frac{a}{2} = \frac{b}{1} = \frac{1}{36}$

un = $\frac{2}{36} = \frac{1}{18}$

b = 1/36

Entonces, ahora como

un = $\frac{1}{x} = \frac{1}{18}$

X = 18

segundo = $\frac{1}{y} = \frac{1}{36}$

y = 36

Por lo tanto, número de días que tardan las mujeres en terminar el trabajo = 18 días

Número de días que tardan los hombres en terminar el trabajo = 36 días.

(iii) Roohi viaja 300 km hasta su casa en parte en tren y en parte en autobús. Tarda 4 horas si recorre 60 km en tren y el resto en autobús. Si recorre 100 km en tren y el resto en autobús, tarda 10 minutos más. Encuentre la velocidad del tren y del autobús por separado.

Solución:

Echemos

Velocidad del tren = x km/h

Velocidad del autobús = y km/h

De acuerdo con la pregunta dada,

$\frac{60}{x} + \frac{240}{y}$ = 4

$\frac{100}{x} + \frac{200}{y} = \frac{25}{6}$

Tomemos 1/x = a y 1/y = b

Aquí, las dos ecuaciones dadas serán las siguientes:

60a + 240b = 4

Dividiéndolo por 4, obtenemos

15a + 60b = 1 -(1)

y,

100a + 200b = 25/6

Dividirlo por 25/6, obtenemos

24a + 48b = 1 -(2)

Ahora, usando el método de multiplicación cruzada,

$\frac{a}{60-48} = \frac{b}{24-15} = \frac{1}{1440-720}$

$\frac{a}{12} = \frac{b}{9} = \frac{1}{720}$

un = $\frac{12}{720}$ = $\frac{1}{60}$

segundo = $\frac{9}{720}$ = $\frac{1}{80}$

Entonces, ahora como

un = $\frac{1}{x}$ = $\frac{1}{60}$

x = 60

segundo = $\frac{1}{y}$ = $\frac{1}{80}$

y = 80

Por lo tanto, la velocidad del tren = 60 km/h

Velocidad del autobús = 80 km/h