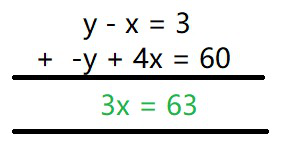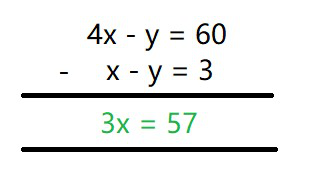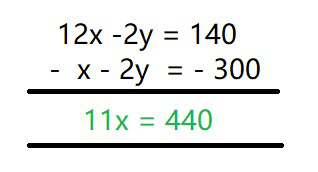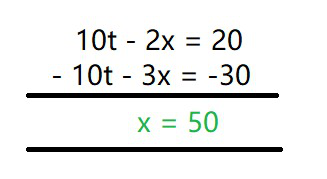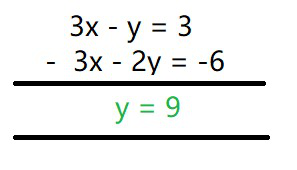Clase 10 Soluciones NCERT – Capítulo 3 Par de ecuaciones lineales en dos variables – Ejercicio 3.7

Pregunta 1. Las edades de dos amigos, Ani y Biju, difieren en 3 años. El padre de Ani, Dharam, tiene el doble de edad que Ani y Biju tiene el doble de edad que su hermana Cathy. Las edades de Cathy y Dharam difieren en 30 años. Encuentra las edades de Ani y Biju.

Solución:

La diferencia de edad entre Ani y Biju = 3 años.

Caso 1: Biju es 3 años mayor que Ani,

y – x = 3

Caso 2: o Ani es 3 años mayor que Biju.

x – y = 3

Dado, la edad del padre de Ani es 30 años más que la edad de Cathy.

Echemos,

la edad de ani = x

y la edad de Biju = y

Entonces, la edad de Dharam será = 2x

Y la edad de la hermana Biju (Cathy) será = $\frac{y}{2}$

CASO 1 (y > x)

Según la condición dada,

y – x = 3 -(1)

y, 2x−y/2 = 30

Multiplícalo por 2, obtenemos

4x – y = 60 -(2)

Sume la ecuación (1) y (2)

3x = 63

x = 63/3

x = 21

Ahora poniendo x = 21 en la ecuación (1), obtenemos

y-21 = 3

y = 24

Por lo tanto, la edad de Ani = 21 años

Y la edad de Biju es = 24 años.

CASO 2: (x > y)

Según la condición dada,

x – y = 3 -(1)

y, 2x−y/2 = 30

Multiplícalo por 2, obtenemos

4x – y = 60 -(2)

Ahora, usando el método de eliminación,

Restar eq(1) de eq(2)

3x = 57

x = 57/3

x = 19

Ahora poniendo x = 19 en la ecuación (1), obtenemos

19 – y = 3

y = 19 – 3

y = 16

Por lo tanto, la edad de Ani = 19 años

Y la edad de Biju es = 16 años.

Pregunta 2. Uno dice: “¡Dame cien, amigo! Entonces seré el doble de rico que tú”. El otro responde: “Si me das diez, seré seis veces más rico que tú”. Dígame cuál es el monto de su (respectivo) capital? [Del Bijaganita de Bhaskara II]

[Pista: x + 100 = 2(y – 100), y + 10 = 6(x – 10)].

Solución:

Sean dos personas como A y B.

Echemos,

Dinero que tiene la persona A = ₹ x

Dinero que la persona B tiene = ₹ y

Entonces, de acuerdo con las condiciones dadas, tenemos

x + 100 = 2(y – 100)

x – 2y = – 300 -(1)

Y

6(x-10) = (y+10)

6x -y = 70 -(2)

Ahora, usando el método de eliminación,

Multiplique eq(2) por 2 y réstele eq(1)

11x = 440

x = 40

Ahora poniendo x = 40 en la ecuación (1), obtenemos

40 – 2 años = – 300

2 años = 300 + 40

y = 340/2

y = 170

Por eso,

La persona A tenía Rs 40 y la persona B tenía Rs 170 con ellos.

Pregunta 3. Un tren recorrió cierta distancia a una velocidad uniforme. Si el tren hubiera ido 10 km/h más rápido, habría tardado 2 horas menos que el tiempo previsto. Y, si el tren fuera 10 km/h más lento; habría tardado 3 horas más de lo previsto. Encuentra la distancia recorrida por el tren.

Solución:

Sea la velocidad del tren = x km/hr

El tiempo que tarda el tren en recorrer una distancia = t horas

La distancia a recorrer = d km.

Como la conocemos,

Distancia recorrida por el tren = Velocidad del tren × Tiempo que tarda en recorrer esa distancia

d = xt -(1)

De acuerdo con la ecuación dada,

re = (x + 10) × (t – 2)

d = xt + 10t – 2x – 20

como d = xt, obtenemos

10t – 2x = 20 -(2)

y ^2ª condición,

re = (x – 10) × (t + 3)

d = xt – 10t + 3x – 30

como d = xt, obtenemos

10t – 3x = -30 -(3)

Ahora, usando el método de eliminación,

Restar eq(3) de eq(2), obtenemos

x = 50 km/h

Ahora poniendo x = 50 en la ecuación (1), obtenemos

10t – 2(50) = 20

10t = 120

t = 12 horas

Ahora, la distancia será = 50 × 12 = 600 km

Por lo tanto, la distancia recorrida por el tren es de 600 km.

Pregunta 4. Los alumnos de una clase se ponen de pie en filas. Si sobran 3 estudiantes seguidos, habría 1 fila menos. Si 3 estudiantes son menos seguidos, habría 2 filas más. Encuentre el número de estudiantes en la clase.

Solución:

Sea el número de filas = x

y, el número de estudiantes en una fila = y.

Número total de estudiantes = Número de filas x Número de estudiantes en una fila = xy -(1)

Aquí, total no. de estudiante será el mismo siempre

Según la condición dada,

Número total de estudiantes = (x – 1)(y + 3)

xy = (x – 1)(y + 3)

xy = xy – y + 3x – 3

3x – y = 3 -(2)

y,

Número total de estudiantes = (x + 2) (y – 3)

xy = xy + 2y – 3x – 6

3x – 2y = -6 -(3)

Ahora, usando el método de eliminación,

Restar eq(3) de eq(2), obtenemos

y = 9

Ahora poniendo y = 9 en la ecuación (1), obtenemos

3x – 9 = 3

3x = 12

x = 4

Número total de estudiantes en una clase = xy

= 4×9

= 36

Por lo tanto, No. de estudiantes = 36

Pregunta 5. En un ∆ABC, ∠C = 3 ∠B = 2 (∠A + ∠B). Encuentra los tres ángulos.

Solución:

Aquí, de acuerdo con las condiciones dadas

3 ∠B = 2 (∠A + ∠B)

3∠B = 2∠A + 2∠B

∠B = 2∠A -(1)

y, ∠C = 3∠B

∠C = 3 (2∠A)

∠C = 6∠A -(2)

Como la conocemos,

∠A + ∠B + ∠C = 180° (Propiedad de la suma de ángulos)

∠A + (2∠A) + (6∠A) = 180° -(De eq(1) y eq(2))

9∠A = 180

∠A = 20°

∠B = 2∠A = 2(20°) = 40°

∠C = 6∠A = 6(20°) = 120°

Por lo tanto, los tres ángulos son 20°, 40° y 120°.

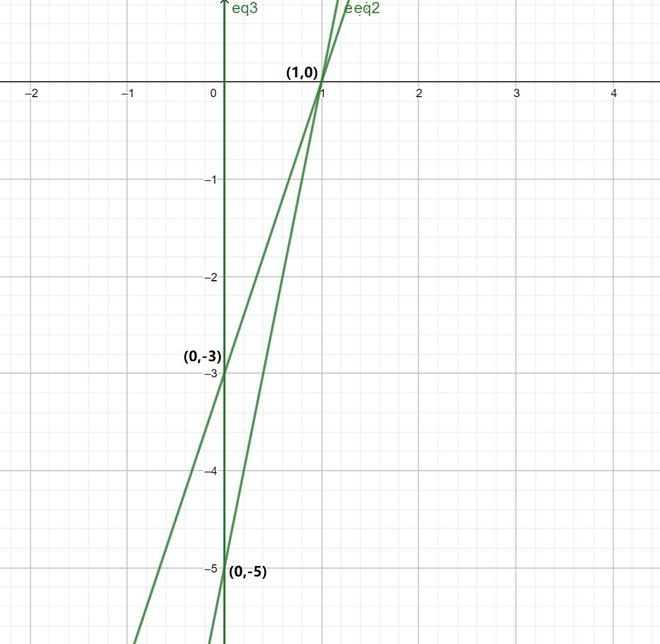
Pregunta 6. Dibujar las gráficas de las ecuaciones 5x – y = 5 y 3x – y = 3. Determinar las coordenadas de los vértices del triángulo formado por estas rectas y el eje y.

Solución:

5x – y = 5 -(1)

3x – y = 3 -(2)

eje y, x = 0 -(3)

Para obtener las coordenadas de los vértices del triángulo formado, vayamos al punto de intersección,

Intersección de la ecuación (1) y (2)

Ahora, usando el método de eliminación,

Reste la ecuación (2) de (1), obtenemos

2x = 2

X = 1

Ahora poniendo x = 1 en eq(1), obtenemos

5(1) – y = 5

y = 0

Entonces, la intersección de los vértices de la ecuación (1) y (2) son (1, 0)

Ahora, Intersección de la ecuación (1) y (3)

Como x = 0 lo sustituye en la ecuación (1), obtenemos

5(0) – y = 5

y = -5

Entonces, la intersección de los vértices (I) y (III) son (0, -5)

Ahora, Intersección de la ecuación (2) y (3)

Como x = 0 lo sustituye en la ecuación (2), obtenemos

3(0) – y = 3

y = -3

Entonces, la intersección de los vértices de la ecuación (2) y (3) son (0,-3)

Por lo tanto, las coordenadas de los vértices del triángulo formado son (1, 0), (0, -5) y (0, -3)

Pregunta 7. Resuelve el siguiente par de ecuaciones lineales:

(i) px + qy = p – q

qx – py = p + q

Solución:

px + qy = p – q -(1)

qx – py = p + q -(2)

Multiplicando p por la ecuación (1) y q por la ecuación (2), obtenemos

pag ² x + pqy = pag ² − pq -(3)

q ² x – pqy = pq + q ² -(4)

Suma la ecuación (3) y (4), obtenemos

pag ² x + q ² x = pag ² + q ²

(pag ² + q ² ) x = pag ² + q ²

x = $\frac{(p^2 + q^2)}{p^2 + q^2}$

X = 1

Ahora poniendo x = 1 en eq(1), obtenemos

p(1) + qy = p – q

qy = pqp

qy = -q

y = -1

(ii) hacha + por = c

bx + ay = 1 + c

Solución:

hacha + por = c -(1)

bx + ay = 1 + c -(2)

Multiplicando a por la ecuación (1) y b por la ecuación (2), obtenemos

a ² x + aby = ac -(3)

b ² x + aby = b + bc -(4)

Reste la ecuación eq(4) de la ecuación (3),

(un ² – ^{segundo 2} ) x = ac − bc– segundo

x = $\frac{(ac − bc- b)}{(a^2 - b^2)}$

x = $\frac{(c(a-b) -b)}{(a^2 - b^2)}$

Ahora poniendo el valor de x en la ecuación (1), obtenemos

hacha + por = c

$a{\frac{(c(a-b) -b)}{(a^2 - b^2)}}$ +por = c

$\frac{(ac(a-b) -b)}{(a^2 - b^2)}$ +por = c

por = $\frac{c-ac(a−b)−ab}{(a^2 - b^2)}$

por = $\frac{(c-ac(a−b)−ab)}{(a^2 - b^2)}$

y = $\frac{(c(a-b)+a)}{(a^2 - b^2)}$

(iii) $\frac{x}{a} - \frac{y}{b} = 0$

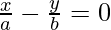
hacha + por = un ² + ^{segundo 2} .

Solución:

$\frac{x}{a} - \frac{y}{b} = 0$ -(1)

Multiplicando la ecuación (1) por ab, obtenemos

bx − ay = 0 -(nuevo 1)

Multiplicando a y b por las ecuaciones (1) y (2) respectivamente, obtenemos

b ² x − aby = 0 -(3)

a ² x + aby = a ³ + ab ³ -(4)

Suma la ecuación (3) y (4), obtenemos

b ² x + a ² x = a ³ + ab ²

x ( ^{segundo 2} + un ² ) = un (un ² + ^{segundo 2} )

x = un

Ahora poniendo x = a en la ecuación (1), obtenemos

b(a) − ay = 0

ab − ay = 0

ay = ab,

y = segundo

(iv) (a – b)x + (a + b) y = a ² – 2ab – b ²

(a + b)(x + y) = a ² + b ²

Solución:

(a – b)x + (a + b) y = a ² – 2ab – b ² -(1)

(a + b)(x + y) = a ² + b ² -(2)

Restamos la ecuación (2) de la ecuación (1), obtenemos

(a – b) x – (a + b) x = (a ² – 2ab – b ² ) – (a ² + b ² )

x(a – segundo – a – b) = – 2ab – 2b ²

− 2bx = − 2b (b + a)

x = segundo + un

Sustituyendo, x = b + a en la ecuación (1), obtenemos

(a + b)(a − b) +y (a + b) = a ² − 2ab – ^{segundo 2}

a ² − b ² + y(a + b) = a ² − 2ab – b ² -(Usando la identidad (a + b)(a – b) = a ² – b ² )

(a + b) y = − 2ab

y = $\frac{-2ab}{a+b}$

(v) 152x – 378y = – 74

–378x + 152y = –604

Solución:

x = $\frac{(189y-137)}{76}$ -(1)

− 378x + 152y = − 604

Sumergiéndolo de 2 en 2, obtenemos

− 189x + 76y = − 302 -(2)

Sustituyendo x en la ecuación (2), obtenemos

−189 $(\frac{(189y-137)}{76})$ +76y=−302

− (189) ² y + 189 × 37 + (76) ² y = − 302 × 76

189 × 37 + 302 × 76 = (189) ² años − (76) ² años

6993 + 22952 = (189 − 76) (189 + 76) y

29945 = (113) (265) año

y = 1

Usando la ecuación (1), obtenemos

x = $\frac{189-37}{76}$

x = 152/76

x = 2

Pregunta 8. ABCD es un cuadrilátero cíclico (ver figura). Encuentra los ángulos del cuadrilátero cíclico.

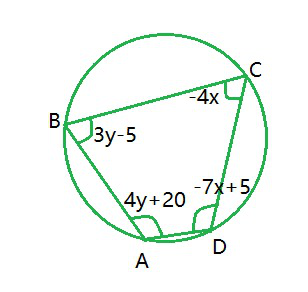
Solución:

Se sabe que la suma de los ángulos opuestos de un cuadrilátero cíclico es 180°

Así, tenemos

∠C+∠A = 180

4y + 20− 4x = 180

− 4x + 4y = 160

x − y = − 40 -(1)

Y, ∠B + ∠D = 180

3y − 5 − 7x + 5 = 180

− 7x + 3y = 180 -(2)

Multiplicando 3 a la ecuación (1), obtenemos

3x − 3y = − 120 -(3)

Sumando la ecuación (2) a la ecuación (3), obtenemos

− 7x + 3x = 180 – 120

− 4x = 60

x = −15

Sustituyendo este valor en la ecuación (1), obtenemos

x − y = − 40

-y−15 = − 40

y = 40-15

y = 25

∠A = 4y + 20 = 20 + 4(25) = 120°

∠B = 3y − 5 = − 5 + 3(25) = 70°

∠C = − 4x = − 4(− 15) = 60°

∠D = 5 – 7x

∠D= 5 − 7(−15) = 110°

Por lo tanto, ∠A, ∠B, ∠C y ∠D son iguales a 120°, 70°, 60° y 110° respectivamente.

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Las edades de dos amigos, Ani y Biju, difieren en 3 años. El padre de Ani, Dharam, tiene el doble de edad que Ani y Biju tiene el doble de edad que su hermana Cathy. Las edades de Cathy y Dharam difieren en 30 años. Encuentra las edades de Ani y Biju.

Pregunta 2. Uno dice: “¡Dame cien, amigo! Entonces seré el doble de rico que tú”. El otro responde: “Si me das diez, seré seis veces más rico que tú”. Dígame cuál es el monto de su (respectivo) capital? [Del Bijaganita de Bhaskara II]

[Pista: x + 100 = 2(y – 100), y + 10 = 6(x ​​– 10)].

Pregunta 4. Los alumnos de una clase se ponen de pie en filas. Si sobran 3 estudiantes seguidos, habría 1 fila menos. Si 3 estudiantes son menos seguidos, habría 2 filas más. Encuentre el número de estudiantes en la clase.

Pregunta 5. En un ∆ABC, ∠C = 3 ∠B = 2 (∠A + ∠B). Encuentra los tres ángulos.

Pregunta 6. Dibujar las gráficas de las ecuaciones 5x – y = 5 y 3x – y = 3. Determinar las coordenadas de los vértices del triángulo formado por estas rectas y el eje y.

Pregunta 7. Resuelve el siguiente par de ecuaciones lineales:

(i) px + qy = p – q

qx – py = p + q

(ii) hacha + por = c

bx + ay = 1 + c

(iii)

hacha + por = un 2 + segundo 2 .

(iv) (a – b)x + (a + b) y = a 2 – 2ab – b 2

(a + b)(x + y) = a 2 + b 2

(v) 152x – 378y = – 74

–378x + 152y = –604

Pregunta 8. ABCD es un cuadrilátero cíclico (ver figura). Encuentra los ángulos del cuadrilátero cíclico.

Deja una respuesta Cancelar la respuesta

[Pista: x + 100 = 2(y – 100), y + 10 = 6(x – 10)].

(iii) $\frac{x}{a} - \frac{y}{b} = 0$

hacha + por = un ² + ^{segundo 2} .

(iv) (a – b)x + (a + b) y = a ² – 2ab – b ²

(a + b)(x + y) = a ² + b ²