Pregunta 1. Completa los espacios en blanco de la siguiente tabla, dado que a es el primer término, d la diferencia común y an el enésimo término del AP
| a | d | norte | un norte | |
| yo | 7 | 3 | 8 | – |
| Yo | -18 | – | 10 | 0 |
| tercero | – | -3 | 18 | -5 |
| IV | -18,9 | 2.5 | – | 3.6 |
| V | 3.5 | 0 | 105 | – |
Solución:
(i) a = 7, d = 3, n = 8
Usando la fórmula AP,
un norte = un + ( n – 1)d
Entonces, un n = 7 + (8 – 1) * 3
un norte = 7 + 21
un norte = 28
(ii) a = -18, d = ?, n = 10, a n = 0
Usando la fórmula AP,
un norte = un + ( n – 1)d
0 = -18 + (10 – 1) * re
18 = 9 * re
re = 2
(iii) a = ?, d = -3, n = 18, a n = -5
Usando la fórmula AP,
un norte = un + ( n – 1)d
-5 = un + (18 – 1) * (-3)
-5 = un – 51
a = -5 + 51
un = 46
(iv) a = -18,9, d = 2,5, n = ?, a n = 3,6
Usando la fórmula AP,
un norte = un + ( n – 1)d
3,6 = -18,9 + (n – 1) * 2,5
3,6 + 18,9 = (n-1) * 2,5
n-1 = 22,5/2,5
n-1 = 9
norte = 10
(v) a = 3.5, d = 0, n = 105, a n = ?
Usando la fórmula AP,
un norte = un + ( n – 1)d
un norte = 3.5 + (105 – 1) * 0
un n = 3,5
Pregunta 2. Elija la opción correcta de las siguientes y justifique
(i) 30° término del AP: 10, 7, 4, ….., es
(A) 97 (B) 77 (C) -77 (D) -87
Solución:
Dado: AP es 10, 7, 4, ……
Ahora encontramos la diferencia común:
Diferencia común (d) = segundo término – primer término
Entonces, d = 7 -10 = -3
El primer término (a) = 10
Número total de términos (n) = 30
Ahora, encontramos el trigésimo término
a 30 (término 30) = a + (n – 1)d
30 = 10 + (30 – 1) * (-3 )
un 30 = 10 – 87
un 30 = -77
Por lo tanto, la opción correcta es C.
(ii) Término 11 de la AP -3, -1/2, 2, ……. es
(A) 28 (B) 22 (C) -38 (D)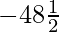 
Solución:
Dado: AP es -3, -1/2, 2, …….
Entonces, primer término (a) = -3
Ahora, encontramos la diferencia común;
Diferencia común (d) = segundo término – primer término
d = -1/2 – (-3)
re = -1/2 + 3
re = 5/2
El undécimo término se puede calcular con la siguiente fórmula
un norte = un + ( n – 1) d
11 = -3 + (11 – 1) * (5/2 )
= -3 + (10) * (5/2)
= -3 + 25
un 11 = 22
Por lo tanto, la opción B es la elección correcta.
Pregunta 3. En los siguientes AP, encuentra el término que falta en los recuadros
(yo) 2, 
, 26
Solución :
Dado: primer término (a) = 2
tercer término (a3) = 26
a 3 se puede calcular usando la fórmula a n = a + (n – 1)d
un 3 = 2 + (3 – 1) * re
26 = 2 + 2d
24 = 2d
re = 12
Entonces un 2 se puede calcular usando la fórmula a n = a + (n – 1)d
un 2 = 2 + (2 – 1) * 12
un 2 = 2 + 12
un 2 = 14
(ii) , 13, , 3
Solución:
Dado:
un 2 = 13
a + (2 – 1)d = 13
a + d = 13 -(1)
un 4 = 3
a + (4 – 1)d = 3
a + 3d = 3 -(2)
Después de resolver la ecuación (1) y (2), obtendrá
d = -5
y a = 18
Ahora encontramos un 3
un 3 = 18 + (3 – 1) * (-5)
un 3 = 18 -10
un 3 = 8
Por lo tanto, los términos que faltan en las casillas cuadradas son 18 y 8.
(iii) 5, , , 
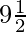
Solución:
Dado:
un = 5
un 4 = 19/2
a + (4 – 1)d = 19/2
5 + 3d = 19/2
3d = (19/2) – 5
3d = 9/2
re = 9/6 = 3/2
Entonces, un 2 = 5 + (2 – 1) * (3/2)
un 2 = 5 + 3/2
un 2 = 13/2
y un 3 = 5 + (3 – 1) * (3/2)
un 3 = 5 + 3
un 3 = 8
Por lo tanto, los términos que faltan en los cuadros cuadrados son 13/2 y 8.
(iv) -4, , , , , 6
Solución:
Dado: a = -4
un 6 = 6
a + (6 – 1)d = 6
-4 + 5d = 6
5d = 10
re = 2
Entonces, a 2 = a + d
un 2 = -4 + 2 = -2
un 3 = un + 2d
un 3 = -4 + 4 = 0
un 4 = un + 3d
un 4 = -4 + 6 = 2
un 5 = un + 4d
un 5 = -4 + 8 = 4
Por lo tanto, los términos que faltan en las casillas cuadradas son -2, 0, 2 y 4.
(v) , 38, , , , -22
Solución:
Dado:
un 2 = 38
a + d = 38 -(1)
un 6 = -22
a + 5d = -22 -(2)
Después de resolver la ecuación (1) y (2), obtendrá
d = -15
y a= 53
Asi que,
un 3 = un + 2d
3 = 53 – 30 = 23
un 4 = un + 3d
un 4 = 53 – 45 = 8
un 5 = un + 4d
un 5 = 53 – 60 = -7
Por lo tanto, los términos que faltan en las casillas cuadradas son 53, 23, 8 y -7.
Pregunta 4. ¿Qué término del AP 3, 8,13, 18, ……. es 78?
Solución:
Dado:
un = 3
d = segundo término – primer término
re = 8 – 3 = 5
y un = 78
n = ?
a + (n – 1)d = 78
3 + (n – 1) * 5 = 78
(n – 1) * 5 = 78 – 3
n – 1 = 75 /5
n = 15 +1
n = 16
Entonces, 78 es el término 16 del AP dado
Pregunta 5. Encuentra el número de términos en cada uno de los siguientes AP
(i) 7, 13, 19, ……, 205
Solución:
Encuentre: n = ?
Dado: a = 7
re = 13 – 7 = 6
un n = 205
a + (n – 1)d = 205
7 + (n – 1) * 6 = 205
(n-1) * 6 = 205-7
n-1 = 198/6
n = 33 + 1
n = 34
Entonces, hay 34 términos en el AP dado
(ii) 18,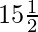 
, 13, ……., -47
Solución:
Encuentre: n = ?
Dado: a = 18
d = 31/2 – 18 = -5/2
un n = -47
18 + (n – 1) * (-5/2) = -47
(n – 1) * (-5/2) = -47 – 18
n-1 = -65 * (-2/5)
n-1 = 130/5
norte = 26 + 1
norte = 27
Por lo tanto, hay 27 términos en el AP dado
Pregunta 6. Comprueba si -150 es un término del AP 11, 8, 5, 2,……..
Solución:
Dado:
un = 11
d = 8 – 11 = -3
Supongamos que -150 es el enésimo término del AP dado, entonces se puede escribir como
a + (n – 1)d = -150
11 + (n – 1) * (-3) =- 150
(n – 1) * (-3) = -150 – 11
n-1 = -161/(-3)
n = 161/3 + 1
n = 164/3
Como puede ver, n no es un número entero. Por lo tanto, -150 no es un término en el AP dado
Pregunta 7. Encuentra el término 31 de un AP cuyo término 11 es 38 y el término 16 es 73.
Solución:
Dado:
un 11 = 38
a + 10 * d = 38 -(1)
un 16 = 73
a + 15 * d = 73 -(2)
Restando la ecuación (1) de la ecuación (2), obtendrás
15 * re – 10 * re = 73 – 38
d = 35/5
re = 7
Después de poner el valor de d en la ecuación (1), obtendrá el valor de a
a = 38 – 70
a = -32
Entonces, a 31 = a + (31 – 1) * d
un 31 = -32 + 30 * 7
un 31 = 178
Por lo tanto, el término 31 del AP dado es 178.
Pregunta 8. En AP consta de 50 términos de los cuales el 3er término es 12 y el último término es 106. Encuentra el término 29.
Solución :
Según la pregunta:
norte = 50
un 3 = 12
a + 2 * d = 12 -(1)
un 50 = 106
a + 49 * d = 106 -(2)
Después de resolver (1) y (2) obtendrá
47 * d = 106 – 12
d = 94/47 = 2
y a = 12 -4 = 8
Entonces, a 29 = a + 28 * d
29 = 8 + 28 * 2
un 29 = 64
Entonces, el término 29 del AP dado será 64.
Pregunta 9. Si los términos 3 y 9 de un AP son 4 y -8 respectivamente. ¿Qué término de este AP es cero?
Solución:
Dado: a 3 = 4
a + 2 * d = 4 -(1)
y un 9 = -8
a + 8 * d = -8 -(2)
Después de resolver (1) y (2), obtendrá
d = -2
y a = 8
Sea el n-ésimo término del AP será cero.
Entonces un n = 0
un + (n – 1) d = 0
8 + (n – 1) * (-2) = 0
n-1 = -8/(-2)
norte = 4 + 1
norte = 5
Por lo tanto, el quinto término del AP dado será cero.
Pregunta 10. Si el término 17 de un AP excede su término 10 por 7. Encuentra la diferencia común.
Solución:
Según la pregunta
un 17 = un 10 + 7
a + (17 – 1)d = a + (10 – 1)d + 7
16 * re = 9 * re + 7
7 * re = 7
re = 1
Por lo tanto, la diferencia común de los AP dados será 1.
Pregunta 11. ¿Qué término del AP 3, 15, 27, 39,….. será 132 más que su término 54?
Solución:
Según la pregunta
re = 15 – 3 = 12
Sea el término n del AP 132 más que su término 54
un norte = un 54 + 132
a + (n – 1)d = a + (54 – 1)d + 132
(n-1)(12) = 53 * 12 + 132
(n – 1) * 12 = 636 + 132
n-1 = 771 / 12
n = 64 + 1
n = 65
Por lo tanto, el término 65 será 132 más que su término 54.
Pregunta 12. Dos AP tienen la misma diferencia común. La diferencia entre su término 100 es 100, ¿cuál es la diferencia entre su término 1000?
Solución:
Sea d la diferencia común de ambos PA y a 1 el primer término de
un AP y un 2 sea el primer término de otro AP
Entonces, un 100 para el primer AP será
un 100 = un 1 + 99d
y un 100 para el segundo AP será
un 100 = un 2 + 99d
De acuerdo con la pregunta, la diferencia entre su término número 100 es 100
Entonces, (a 1 + 99d) – (a 2 + 99d) = 100
un 1 – un 2 = 100 -(1)
Ahora a100 para el primer AP será
un 1000 = un 1 + 999d
y 1000 para el segundo AP será
un 1000 = un 2 + 999d
La diferencia entre su término 1000 será
= (un 1 + 999d) – (un 2 + 999d)
= un 1 – un 2
= 100 -(de (1) a 1 -a 2 = 100)
Por lo tanto, la diferencia entre su término 1000 será 100.
Pregunta 13. ¿Cuántos números de tres dígitos son divisibles por 7?
Solución:
Primer número de tres dígitos que es divisible por 7 = 105
Entonces, el primer término del AP (a) = 105
y diferencia común (d) = 7
El último número de tres dígitos que es divisible por 7 = 994
Entonces AP se verá como 105, 112, 119,………, 994
Sean n números de tres cifras entre 105 y 994
Tienes un n = 994
a + (n – 1)d = 994
105 + (n – 1) * 7 = 994
(n-1) * 7 = 994-105
n-1 = 889/7
n = 127 + 1
n = 128
Por lo tanto, hay 128 números de tres dígitos que son divisibles por 7.
Pregunta 14. ¿Cuántos múltiplos de 4 hay entre 10 y 250?
Solución:
Dado:
12 es el número mínimo divisible por 4 entre 10 y 250.
Entonces, a = 12
re = 4
248 es el número más alto que es divisible por 4 entre 10 y 250.
Entonces un n = 248
a + (n – 1)d = 248
12 + (n – 1) * 4 = 248
(n-1) * 4 = 236
n-1 = 59
norte = 60
Por lo tanto, hay 60 múltiplos de 4 entre 10 y 250.
Pregunta 15. Para qué valor de n, son los n-ésimos términos de dos APs 63, 65, 67,…. y 3, 10, 17,….. ¿iguales?
Solución:
Para AP 63, 65, 67,…..
a = 63 y d = 65 – 63 = 2
El término n para este AP será
un norte = 63 + (n – 1) * 2
Para AP 3, 10, 17, ….
a = 3 y d = 10 – 3 = 7
El término n para este AP será
un norte = 3 + (n – 1) * 7
De acuerdo con la pregunta, los n-ésimos términos de ambos AP son iguales
Entonces, 63 + (n – 1) * 2 = 3 + (n – 1) * 7
60 = (n – 1) * 5
n-1 = 12
norte = 13
Por lo tanto, 13 de ambos AP son iguales.
Pregunta 16. Determina el AP cuyo tercer término es 16 y el 7° término excede al 5° término en 12.
Solución:
un 3 = 16
a + 2d = 16 -(1)
y un 7 = un 5 + 12
a + 6d = a + 4d + 12
2d = 12
re = 6
Al poner el valor de d en la ecuación (1), obtendrá
a = 16 – 12
un = 4
Entonces, AP se verá como 4, 10, 16, 22, 28,…..
Pregunta 17. Halla el vigésimo término del último término del AP 3, 8, 13,………, 253
Solución:
re = 8 – 3 = 5
En orden inverso, el AP será
253, 248, ………. 13, 8, 3
Ahora para este AP
a = 253 y d = 248 – 253 = -5
Así que el término 20 será
un 20 = un + 19d
20 = 253 + 19 * (-5 )
un 20 = 158
Por lo tanto, el vigésimo término desde el último término para el AP dado será 158.
Pregunta 18. La suma de los términos 4 y 8 de un AP es 24 y la suma de los términos 6 y 10 es 44. Encuentra los primeros tres términos del AP.
Solución:
Dado: un 4 + un 8 = 24
a + 3d + a + 7d = 24
2a + 10d = 24
a + 5d = 12 -(1)
y un 6 + un 10 = 44
a + 5d + a + 9d = 44
2a + 14d = 44
a + 7d = 22 -(2)
De (1) y (2), obtendrá
re = 5
y a = -13
Entonces a 2 = a + d
un 2 = -13 + 5 = -8
un 3 = un + 2d
un 3 = -13 + 10 = -3
Por lo tanto, los primeros tres términos del AP son -13, -8, -3
Pregunta 19. Subba Rao comenzó a trabajar en 1995 con un salario anual de 5000 rupias y recibió un incremento de 200 rupias cada año. ¿En qué año sus ingresos alcanzaron Rs 7000?
Solución:
Como, el salario de Subba Rao aumenta en una cantidad fija cada año, por lo tanto
esto formará un AP con primer término (a) = 5000 y diferencia común (d) d = 200
un n = 7000
a +(n – 1)d = 7000
5000 + (n – 1) * 200 = 7000
n-1 = 2000/200
norte = 10 + 1
n = 11
Por lo tanto, el salario será de 7000 en el año 11.
Pregunta 20. Ramkali ahorró 5 rupias en la primera semana de un año y luego aumentó su ahorro semanal en 1,75. Si en la semana n sus ahorros semanales se convierten en Rs 20,75, encuentre n.
Solución:
Como el ahorro se incrementa en una cantidad fija, esto formará un AP en el que
Primer término (a) = 5
Diferencia común (d) = 1,75
un n = 20,75
a + (n – 1)d = 20,75
5 + (n – 1) * (1,75) = 20,75
(n – 1) * (1,75) = 20,75 – 5
n-1 = 15,75/1,75
norte = 9 + 1
norte = 10
Por lo tanto, n = 10