Teorema 6.1:
Si se traza una línea paralela a un lado de un triángulo para cortar los otros dos lados en puntos distintos, los otros dos lados se dividen en la misma proporción.
Teorema 6.2:
Si una recta divide dos lados cualesquiera de un triángulo en la misma proporción, entonces la recta es paralela al tercer lado.
Pregunta 1. En la Figura, (i) y (ii), DE || ANTES DE CRISTO. Encuentre EC en (i) y AD en (ii).
Solución:
(i) Aquí, en △ ABC,
ES || antes de Cristo
Entonces, de acuerdo con el Teorema 6.1
⇒
⇒CE =
CE = 2 cm
Por lo tanto, CE = 2 cm.
(ii) Aquí, en △ ABC,
Entonces, según el Teorema 6.1, si DE || antes de Cristo
⇒
⇒AD =
DA = 2,4 cm
Por lo tanto, AD = 2,4 cm.
Pregunta 2. E y F son puntos de los lados PQ y PR respectivamente de un ∆ PQR. Para cada uno de los siguientes casos, indique si EF || QR :
(i) PE = 3,9 cm, EQ = 3 cm, PF = 3,6 cm y FR = 2,4 cm
Solución:
De acuerdo con el Teorema 6.2,
Si una recta divide dos lados cualesquiera de un triángulo en la misma proporción, entonces la recta es paralela al tercer lado.
Por lo tanto, vamos a comprobar las proporciones
Aquí, en △ PQR,
= 1.3 …………………………(yo)
= 1.5 …………………………(ii)
Como,
Por lo tanto, EF no es paralelo a QR.
(ii) PE = 4 cm, QE = 4,5 cm, PF = 8 cm y RF = 9 cm
Solución:
De acuerdo con el Teorema 6.2,
Si una recta divide dos lados cualesquiera de un triángulo en la misma proporción, entonces la recta es paralela al tercer lado.
Por lo tanto, vamos a comprobar las proporciones
Aquí, en △ PQR,
………………………(i)
…………………………(ii)
Como,
Por lo tanto, EF es paralelo a QR.
(iii) PQ = 1,28 cm, PR = 2,56 cm, PE = 0,18 cm y PF = 0,36 cm
Solución:
EQ = PQ – PE = 1,28 – 0,18 = 1,1
y, FR = PR – PF = 2,56 – 0,36 = 2,2
De acuerdo con el Teorema 6.2,
Si una recta divide dos lados cualesquiera de un triángulo en la misma proporción, entonces la recta es paralela al tercer lado.
Por lo tanto, vamos a comprobar las proporciones
Aquí, en △ PQR,
………………………(i)
…………………………(ii)
Como,
Por lo tanto, EF es paralelo a QR.
Pregunta 3. En la Figura, si LM || CB y LN || CD, prueba que
Solución:
Aquí, en △ ABC,
De acuerdo con el Teorema 6.1, si LM || CB
entonces,
……………………………….(yo)
y, en △ ADC,
De acuerdo con el Teorema 6.1, si LN || CD
luego,
……………………………….(II)
De (I) y (II), concluimos que
Por lo tanto Probado !!
Pregunta 4. En la Figura, DE || AC y DF || AE. Pruebalo
Solución:
Aquí, en △ ABC,
De acuerdo con el Teorema 6.1, si DE || C.A.
entonces,
……………………………….(yo)
y, en △ ABE,
De acuerdo con el Teorema 6.1, si DF || AE
luego,
……………………………….(II)
De (I) y (II), concluimos que
Por lo tanto Probado !!
Pregunta 5. En la figura, DE || OQ y DF || O. Demuestre que EF || QR.
Solución:
Aquí, en △ POQ,
De acuerdo con el Teorema 6.1, si DE || OQ
entonces,
……………………………….(yo)
y, en △ POR,
De acuerdo con el Teorema 6.1, si DF || O
luego,
……………………………….(II)
De (I) y (II), concluimos que
…………………………………(III)
Según Therem 6.2 y eqn. (III)
FE || QR, en △ PQR
Por lo tanto Probado !!
Pregunta 6. En la figura, A, B y C son puntos en OP, OQ y OR respectivamente tales que AB || PQ y AC || relaciones públicas Demuestra que BC || QR.
Solución:
Aquí, en △ POQ,
De acuerdo con el Teorema 6.1, si AB || PQ
entonces,
……………………………….(yo)
y, en △ POR,
De acuerdo con el Teorema 6.1, si AC || relaciones públicas
luego,
……………………………….(II)
De (I) y (II), concluimos que
…………………………………(III)
Según Therem 6.2 y eqn. (III)
antes de Cristo || QR, en △ OQR
Por lo tanto Probado !!
Pregunta 7. Usando el Teorema 6.1, demuestre que una línea trazada a través del punto medio de un lado de un triángulo paralelo a otro lado biseca el tercer lado.
Solución:
Dado, en ΔABC, D es el punto medio de AB tal que AD=DB.
Una recta paralela a BC corta a AC en E
Entonces, DE || ANTES DE CRISTO.
Tenemos que demostrar que E es el punto medio de AC.
Como, AD=BD
⇒
= 1 …………………………. (YO)
Aquí, en △ ABC,
De acuerdo con el Teorema 6.1, si DE || antes de Cristo
luego,
……………………………….(II)
De (I) y (II), concluimos que
= 1
AE = CE
E es el punto medio de AC.
Por lo tanto demostrado !!
Pregunta 8. Usando el Teorema 6.2, demuestre que la línea que une los puntos medios de dos lados cualesquiera de un triángulo es paralela al tercer lado.
Solución:
Dado, en ΔABC, D y E son los puntos medios de AB y AC respectivamente
AD=BD y AE=EC.
Tenemos que demostrar que: DE || ANTES DE CRISTO.
Como, AD=BD
⇒
y, AE=EC
⇒
De (I) y (II), concluimos que
Según Therem 6.2 y eqn. (III)
ES || BC, en △ ABC
Por lo tanto Probado !!
Pregunta 9. ABCD es un trapecio en el que AB || DC y sus diagonales se intersecan en el punto O. Demuestra que
Solución:
Desde el punto O trazar una recta EO que toque a AD en E, de tal forma que,
EO || CC || AB
Aquí, en △ ADB,
De acuerdo con el Teorema 6.1, si AB || EO
entonces,
……………………………….(yo)
y, en △ ADC,
De acuerdo con el Teorema 6.1, si AC || relaciones públicas
luego,
……………………………….(II)
De (I) y (II), concluimos que
Después de reorganizar, obtenemos
Por lo tanto Probado !!
Pregunta 10. Las diagonales de un cuadrilátero ABCD se cortan en el punto O tal que
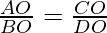. Demuestra que ABCD es un trapecio.
Solución:
Desde el punto O trazar una recta EO que toque a AD en E, de tal forma que,
EO || CC || AB
Aquí, en △ ADB,
De acuerdo con el Teorema 6.1, si AB || EO
entonces,
(Dado)
(Después de reorganizar) ………………………………..(II)
De (I) y (II), concluimos que
Según Therem 6.2 y eqn. (III)
EO || DC y también EO || AB
⇒ AB || CORRIENTE CONTINUA.
Por lo tanto, el cuadrilátero ABCD es un trapecio con AB || CD.