Clase 10 Soluciones NCERT – Capítulo 6 Triángulos – Ejercicio 6.6

Pregunta 1. En la figura, PS es la bisectriz de ∠QPR de Δ PQR. Pruebalo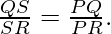 $\frac{QS}{SR} = \frac{PQ}{PR}.$

Solución:

Dado: PS es la bisectriz del ángulo de ∠QPR.

Probar: $\frac{QS}{SR} = \frac{PQ}{PR}$

Construcción: Dibuje RT∥ST para cortar OP provisto en T.

Prueba: dado que PS∥TR y PR los cortan, por lo tanto tenemos,

∠1 = ∠3 ——[ángulo interior alterno] 1

∠1 = ∠4 ——[ángulo correspondiente] 2

Pero ∠1 = ∠2 [dado]

De 1 y 2

∴∠3=∠4

En ∆PTR,

PT = PR [los lados opuestos al ángulo igual son iguales] 3

Ahora en ∆QRT, tenemos

$\frac{QS}{SR} = \frac{PQ}{PT}$ ———-[por BPT]

$\frac{QS}{SR} = \frac{PQ}{PR}$ ———[de 3]

Pregunta 2. En la Fig., D es un punto en la hipotenusa AC de Δ ABC, tal que BD ⊥ AC, DM ⊥ BC y

DN ⊥ AB. Pruebalo:

(i) DM ² = DN.MC

(ii) DN ² = DM.AN

Solución:

Dado: BD ⊥ AC, DM ⊥ BC y DN ⊥ AB

Probar:

(i) DM ² = DN.MC

(ii) DN ² = DM.AN

Prueba: tenemos AB⊥BC y DM⊥BC

Entonces, AB || MD

De manera similar, tenemos CB⊥AB y DN ⊥ AB

Por lo tanto, CB || DN

Por lo tanto, BMD DN es un triángulo

∴BM=DN o DM=ND

En ∆DMO,

∠1+ ∠2+ ∠DMB=180 ———–[propiedad de la suma de ángulos del triángulo]

∠1+ ∠2+90=180

∠1+ ∠2=180-90

∠1+ ∠2=90 ——————-1

De manera similar, en ∆DMC,

∠3+ ∠4=90° _______2

∴ de 1 y 2

∠1+ ∠2=∠2+ ∠3

∠1=∠3

De 2 y 3

∠3+ ∠4=∠2+ ∠3

∠4=∠2

Ahora en ∆BMD y ∆DMC,

∠1=∠3

∠2=∠4

∴∆BMD~∆DMC ——-(criterios de similitud AA)

$\frac{BM}{DM} = \frac{MD}{MC}$

$\frac{DN}{DM} = \frac{MD}{MC}$

DM ² =DN*MC

II) procediendo como en (i), podemos probar que ∆BND~∆DNA

$\frac{BN}{DN} = \frac{ND}{NA}$

$\frac{DM}{DN} = \frac{ND}{NA}$ [BN=NA]

DN ² = MN*MC

Pregunta 3. En la figura, ABC es un triángulo en el que se producen ∠ABC > 90° y AD ⊥ CB. Demostrar que AC ²= AB ²+ BC ²+ 2 BC.BD.

Dado: En ∆ABC, ∠ABC > 90° y AD⊥CB siempre.

Para probar: (AC) ² = AB ² +BC ² + 2 BC.BD

Prueba: En ∆ADB por el teorema de Pitágoras,

CA ² = AD ² + AB ²

(AC) ² = (AD) ² + (DB) ² ———1

En ∆ADC por el teorema de Pitágoras,

(CA) ² = (AD) ² + (CC) ² ———2

AC ² = AD ² + DB ² ———1

AC ² = AD ² +(DB) ² +2*DB*BC

AC ² = AD ² +(DB) ² +BC ² +2*DB*BC

Pregunta 4. En la figura, ABC es un triángulo en el que ∠ABC < 90° y AD ⊥ BC. Demuestre que AC ²= AB ²+ BC ²– 2BC.BD.

Solución:

Dado: En ∆ABC, ∠ABC < 90° y AD ⊥ BC.

Para probar: AC ² = AB ² + BC ² – 2*BC.BD

Demostración: En el triángulo ADB, por el teorema de Pitágoras

AB ² =AD ² +BD ² ———1

En el triángulo ADC, por el teorema de Pitágoras

CA ² =AD ² +CC ² ———2

AC ² = AD ² + BC ² + BD ²

AC ² =AD ² + BC ² +BD ² – 2*BC*BD

AC ² =AB ² + BD ² +BC ² – 2*BC*BD

AC ² = AB ² + BC ² – 2BC.BD

Pregunta 5. En la figura, AD es una mediana de un triángulo ABC y AM ⊥ BC. Pruebalo:

(i) AC ² = AD ² + BC.DM + (BC/2) ²

(ii) AB ² = AD ² – BC.DM + (BC/2) ²

(iii) AC ² + AB ² = 2 AD ² + 1/2 BC ²

Dado: En ∆ABC, AD es una mediana, AM ⊥ BC.

Pruebalo:

(i) AC ² = AD ² + BC.DM + (BC/2) ²

(ii) AB ² = AD ² – BC.DM + (BC/2) ²

(iii) AC ² + AB ² = 2 AD ² + 1/2 BC ²

Prueba: i) En obtuso ∆ADC,∠D>90°

CA ² = AD ² + CC ² +2DC.DM

CA ² = DA ² +(BC/2) ² +2(BC/2).DM

AC ² = AD ² + (BC/2) 2 + BC.DM

O AC ² = AD ² +BC.DM+(BC/2) ²

II) En el triángulo agudo ABD,

∠D>90°

AB ² = AD ² + BD ² + 2BD.DM

AB2 = AD2 ⁺ (BC/2) ²^-2 (BC/2).DM

^AB2 = AD2 +(BC/2 ⁾² -BC.DM

O

AB ² = AD ² -BC.DM +(BC/2) ²

iii) Sumando i y ii

AC ² +AB ² =AD ² +BC.DM+(BC/2) ² +AD ² -BC.DM +(BC/2) ²

= 2 AD ² +BC/4 ² +BC/4 ²

= 2AD ² +1/2.BC/4 ²

= 2AD ² + BC ²

Pregunta 6. Demuestra que la suma de los cuadrados de las diagonales de un paralelogramo es igual a la suma de los cuadrados de sus lados.

Solución:

Dado: ||gm ABCD y diagonales BD y AC

Para probar: AB ² +BC ² +CD ² +AD ² =AC ² +BD ²

Prueba: las diagonales de ||gm se bisecan entre sí en el punto medio

Solución: En ∆ABC, BO es mediana

∴AB ² +BC ² =2BO ² +1/2AC ² ———1

En ∆ADC, DO es mediana

∴AD ² +DC ² = 2DO ² +1/2AC ² ———2

sumando 1 y 2

AB ² +BC ² +AD ² +DC ² =2BO ² +1/2AC ² +2DO ² +1/2AC ²

=2.(1/2.BD) ² +1/2AC ² +2(1/2BD) ² +1/2AC ²

=2.BD/4 ² +1/4AC ² +2.BD/4 ² +1/2AC ²

=BD ² /2+1/2AC ² +BD ² /2+1/2AC ²

=BD ² +AC ²

Pregunta 7. En la Fig., dos cuerdas AB y CD se cortan en el punto P. Demuestre que:

(i) Δ APC ~ Δ DPB

(ii) AP.PB = CP.DP

Solución:

Dado: las cuerdas AB y CD se cortan en el punto P.

Para probar: (i) Δ APC ~ Δ DPB (ii) AP.PB = CP.DP

Prueba: En ∆ABC y ∆DPB,

∠1=∠2 ——-[ángulo verticalmente opuesto]

∠A=∠D ——-[los ángulos en el mismo segmento del círculo son iguales]

i) ∴∆APC~∆DPB (criterios de similitud AA)

ii) $\frac{AP}{DB} = \frac{CP}{PB}$

AP*PB=CP*DP

Pregunta 8. En la figura, dos cuerdas AB y CD de un círculo se intersecan en el punto P (cuando se produce) fuera del círculo. Pruebalo

(i) Δ PAC ~ Δ PDB

(ii) PA.PB = PC.PD

Solución:

i) En ∆PAC y ∆PDB,

∠P=∠P ———[común]

∠1+∠2=180° ——–[ángulo de par lineal]

∠2=180°+∠1

∠2+∠3=180° ——[la suma de los ángulos opuestos de un cuadrilátero cíclico es 180°]

∠3=180°-180°+∠1

∠3=∠1 ————2

∠1=∠3 ———–[forma 2]

∴∆APC~∆PDB ———[Criterios de similitud AA]

ii) $\frac{PA}{PD} = \frac{PC}{PB}$

PA*PD = PC*PB

Pregunta 9. En la Fig., D es un punto en el lado BC de Δ ABC tal que 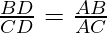$\frac{BD}{CD} = \frac{AB}{AC}$ . Demuestra que AD es la bisectriz de ∠BAC.

Solución:

Construcción: Producir BA a E tal que AE=AC se une a CE.

Prueba: En ∆AEC,

Como AE=AC

∴∠1=∠2 ——[Ángulo opuesto a los lados iguales de ∆are=]

$\frac{BD}{CD} = \frac{AB}{AC}$

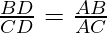
$\frac{BD}{CD} = \frac{AB}{AE}$ —-(POR CONSTRUCCIÓN)

Por el contrario de BPT

AD||CE

Y AC es una transversal entonces

∠3=∠1 ——-[ángulos correspondientes]

∠4=∠2 ——-[ángulos interiores alternos]

Pero ∠1=∠2 ——–[por construcción]

∴AD biseca ∠BAC internamente

Pregunta 10. Nazima está pescando con mosca en un arroyo. La punta de su caña de pescar está a 1,8 m sobre la superficie del agua y la mosca en el extremo de la cuerda descansa sobre el agua a 3,6 m de distancia y a 2,4 m de un punto directamente debajo de la punta de la caña. Suponiendo que su hilo (desde la punta de la caña hasta la mosca) está tenso, ¿cuánto hilo le queda (ver figura)? Si tira de la cuerda a razón de 5 cm por segundo, ¿cuál será la distancia horizontal de la mosca a ella después de 12 segundos?

Solución:

En ∆ABC,

AC es una string

Por el teorema de Pitágoras,

CA ² =AB ² +BC ²

CA ² =AB ² +BC ²

CA ² = (1.8) ² + (2.4) ²

(CA) ² =3,24+5,76

CA=√9

CA = 3m

∴Longitud de la cuerda que tiene = 3m

=5cm/seg*12seg

= 60 cm

=60/100 =0,6m

AP=AC-0.6

=3-06

= 2,4 metros

Ahora en ∆ABP por el teorema de Pitágoras,

(AP) ² = (AB) ² + (PB) ²

(2.4) ² = (1.8) ² + (PB) ²

5,76=3,24 + (PB) ²

5,76=3,24 + (PB) ²

2.52=(PB) ²

√2.52=PB

1.59=PB

PD=PB+BD

DP=1,59+1,2

PD=2,79 m ———(aprox.)

Por lo tanto, la distancia horizontal de la mosca de nazima de los 12 segundos en 2,79 m.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. En la figura, PS es la bisectriz de ∠QPR de Δ PQR. Pruebalo

Pregunta 2. En la Fig., D es un punto en la hipotenusa AC de Δ ABC, tal que BD ⊥ AC, DM ⊥ BC y

Pregunta 3. En la figura, ABC es un triángulo en el que se producen ∠ABC > 90° y AD ⊥ CB. Demostrar que AC 2 = AB 2 + BC 2 + 2 BC.BD.

Pregunta 4. En la figura, ABC es un triángulo en el que ∠ABC < 90° y AD ⊥ BC. Demuestre que AC 2 = AB 2 + BC 2 – 2BC.BD.

Pregunta 5. En la figura, AD es una mediana de un triángulo ABC y AM ⊥ BC. Pruebalo:

Pregunta 6. Demuestra que la suma de los cuadrados de las diagonales de un paralelogramo es igual a la suma de los cuadrados de sus lados.

Pregunta 7. En la Fig., dos cuerdas AB y CD se cortan en el punto P. Demuestre que:

Pregunta 8. En la figura, dos cuerdas AB y CD de un círculo se intersecan en el punto P (cuando se produce) fuera del círculo. Pruebalo

Pregunta 9. En la Fig., D es un punto en el lado BC de Δ ABC tal que . Demuestra que AD es la bisectriz de ∠BAC.

Deja una respuesta Cancelar la respuesta

Pregunta 1. En la figura, PS es la bisectriz de ∠QPR de Δ PQR. Pruebalo $\frac{QS}{SR} = \frac{PQ}{PR}.$

Pregunta 3. En la figura, ABC es un triángulo en el que se producen ∠ABC > 90° y AD ⊥ CB. Demostrar que AC ²= AB ²+ BC ²+ 2 BC.BD.

Pregunta 4. En la figura, ABC es un triángulo en el que ∠ABC < 90° y AD ⊥ BC. Demuestre que AC ²= AB ²+ BC ²– 2BC.BD.

Pregunta 9. En la Fig., D es un punto en el lado BC de Δ ABC tal que $\frac{BD}{CD} = \frac{AB}{AC}$ . Demuestra que AD es la bisectriz de ∠BAC.