Soluciones NCERT Clase 10 – Capítulo 7 Geometría de coordenadas – Ejercicio 7.2

Posted on by Rudeus Greyrat

Pregunta 1. Encuentra las coordenadas del punto que divide la unión de (–1, 7) y (4, –3) en la razón 2 : 3.

Solución:

Sea el punto P (x,y) que divide a la recta AB en la razón 2:3

dónde,

m = 2 y n = 3

x 1 = -1 y y 1 = 7

x2 = 4 y y2 = -3

entonces, la coordenada x de P será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{2*4 + 3*(-1)}{ 2+3}

x = \frac{5}{5}

X = 1

y ahora, la coordenada y de P será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(2*(-3) + 3*7)}{2+3}

y = \frac{15}{5}

y = 3

Por lo tanto, la coordenada de P(x,y) es (1,3)

Pregunta 2. Halla las coordenadas de los puntos de trisección del segmento de recta que une (4, –1) y (–2, –3).

Solución:

Sea el punto P (x 1 ,y 1 ) y Q(x 2 ,y 2 ) que triseca la línea.

Entonces, podemos concluir que

P divide la línea AB en la razón 1:2.

y Q divide la línea AB en la razón 2:1.

  • Para p

m = 1 y n = 2

x 1 = 4 y y 1 = -1

x2 = -2 y y2 = -3

entonces, la coordenada x de P será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(1*(-2) + 2*4)}{1+2}

x = 2

y ahora, la coordenada y de P será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(1*(-3) + 2*(-1))}{ 1+2}

y = \frac{-5}{3}

Por lo tanto, la coordenada de P es (2, \mathbf{\frac{-5}{3}} ).

  • para Q

m = 2 y n = 1

x 1 = 4 y y 1 = -1

x2 = -2 y y2 = -3

entonces, la coordenada x de Q será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(2*(-2) + 1*4)}{2+1}

x = 0

y ahora, la coordenada y de Q será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(2*(-3) + 1*(-1)}{ 2+1}

y = \frac{-7}{3}

Por lo tanto, la coordenada de Q es (0, \mathbf{\frac{-7}{3}} ).

Pregunta 3. Para realizar las actividades del Día del Deporte, en el terreno de su escuela de forma rectangular ABCD, se han dibujado líneas con tiza en polvo a una distancia de 1 m cada una. Se han colocado 100 macetas a una distancia de 1 m entre sí a lo largo de AD, como se muestra en la Fig. 7.12. Niharika corre 1/4 de la distancia AD en la segunda línea y coloca una bandera verde. Preet corre 1/5 de la distancia AD en la octava línea y coloca una bandera roja. ¿Cuál es la distancia entre ambas banderas? Si Rashmi tiene que colocar una bandera azul exactamente a medio camino entre el segmento de línea que une las dos banderas, ¿dónde debería colocar su bandera?

Solución:

Como los datos dados,

AD = 100 m

Preet colocó bandera roja a  \frac{1}{5}  la distancia AD

= ( \frac{1}{5}  ×100) metro

= 20m desde el punto de partida de la 8ª línea.

Por lo tanto, las coordenadas de este punto serán (8, 20).

Del mismo modo, Niharika colocó la bandera verde al  \frac{1}{4} final de la distancia AD

= ( \frac{1}{4}  ×100) metro

= 25m desde el punto de inicio de la 2ª línea.

Por lo tanto, las coordenadas de este punto serán (2, 25).

La distancia entre estas banderas se puede calcular usando la fórmula de distancia,

Distancia entre dos puntos de coordenadas (x 1 ,y 1 ) y (x 2 ,y 2 ) = √((x 1 -x 2 ) 2 + (y 1 -y 2 ) 2 )

Distancia entre estas banderas = √((8-2) 2 + (20-25) 2 )

= √(6 2 + 5 2 )

Distancia entre estas banderas = √61 m

Ahora, Rashmi tiene que colocar una bandera azul exactamente a la mitad entre las dos banderas. Por lo tanto, colocará la bandera azul en el punto medio de la línea que une estos puntos. dónde,

metro = norte = 1

(x 1 , y 1 ) = (8, 20)

(x2 , y2 ) = (2, 25)

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(1*2 + 1*8)}{1+1}

x = \frac{10}{2}

x = 5

y ahora, la coordenada y de Q será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(1*25 + 1*20)}{1+1}

y = \frac{45}{2}

y = 22.5

Por lo tanto, Rashmi debería colocar su bandera azul a 22,5 m en la quinta línea.

Pregunta 4. Halla la razón en que el segmento de recta que une los puntos (– 3, 10) y (6, – 8) se divide por (– 1, 6).

Solución:

Consideremos la razón en la que el segmento de recta que une (-3, 10) y (6, -8) se divide por el punto (-1, 6) siendo k :1.

m = k y n = 1

(x 1 ,y 1 ) = (3, 10) y (x2,y2) = (6,-8)

x = -1

x =\mathbf{\frac{mx_2 + nx_1}{m+n}}

-1 = \frac{(k*6 + 1*3)}{k+1}

-1(k+1) = 6k+3

k = \mathbf{\frac{2}{7}}

Por lo tanto, la relación requerida es 2:7.

Pregunta 5. Encuentra la razón en la que el segmento de línea que une A(1, – 5) y B(– 4, 5) está dividido por el eje x. Halla también las coordenadas del punto de división.

Solución:

Sea el punto P que divide el segmento de recta que une A (1, – 5) y B (– 4, 5) en la razón m : 1.

Por lo tanto, las coordenadas del punto de división, digamos P(x, y) y,

Sabemos que la coordenada y de cualquier punto en el eje x es 0.

P(x, 0)

m = m y n = 1

(x 1 , y 1 ) = (1, -5)

(x 2 , y 2 ) = (-4,5)

entonces, como la coordenada y de P es 0,

y =\mathbf{\frac{mi_2 + ny_1}{m+n}}

0 = \frac{(m*5 + 1*(-5))}{m+1}

5m-5=0

metro = 1

Entonces, el eje x divide el segmento de línea en la proporción 1:1 .

y, x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(1*(-4) + 1*1)}{1+1}

x = \frac{-3}{2}

Por lo tanto, la coordenada de P es ( \mathbf{\frac{-3}{2}},0).

Pregunta 6. Si (1, 2), (4, y), (x, 6) y (3, 5) son los vértices de un paralelogramo tomado en orden, encuentra x e y.

Solución:

Sean P, Q, R y S los puntos de un paralelogramo: P(1,2), Q(4,y), R(x,6) y S(3,5).

Punto medio de PR = Punto medio de QS ( Las diagonales de un paralelogramo se bisecan entre sí, el punto medio O es el mismo )

  • Punto medio de PR

m = 1 y n = 1

(x 1 , y 1 ) = (1, 2)

(x2 ,y2 ) = (x,6)

entonces, la coordenada x de O será,

xo =  _\mathbf{\frac{mx_2 + nx_1}{m+n}}

xo =  _\frac{(1*x) + 1*1)}{1+1}

xo =  _\frac{(x+1)}{2}

y ahora, la coordenada y de O será,

yo = _ \mathbf{\frac{mi_2 + ny_1}{m+n}}

yo = _ \frac{(1*6 + 1*2)}{ 1+1}

año = 4

Entonces, la coordenada de O es ( \mathbf{\frac{(x+1)}{2}} , 4) ……………..(1)

  • Para punto medio QS

m = 1 y n = 1

(x 1 ,y 1 ) = (3,5)

(x 2 , y 2 ) = (4, y)

entonces, la coordenada x de O será,

xo = _ \mathbf{\frac{mx_2 + nx_1}{m+n}}

xo =  _\frac{(1*4) + 3*1)}{1+1}

xo =  _\frac{7}{2}

y ahora, la coordenada y de O será,

yo = _ \mathbf{\frac{mi_2 + ny_1}{m+n}}

yo = _ \frac{(1*y + 1*5)}{1+1}

yo = _ \frac{(5+y)}{2}

además, la coordenada de O es  (\mathbf{\frac{7}{2},\frac{(5+y)}{2}})……………..(2)

De (1) y (2)

\frac{(1+x)}{2} = \frac{7}{2}  y 4 = \frac{(5+y)}{2}

x = 6 y y = 3

Pregunta 7. Encuentra las coordenadas de un punto A, donde AB es el diámetro de un círculo cuyo centro es (2, – 3) y B es (1, 4).

Solución:

Sean las coordenadas del punto A (x, y).

El punto medio de AB es C(2, – 3), que es el centro del círculo.

y, Coordenada de B = (1, 4)

Para el punto medio de dos puntos (x 1 ,y 1 ) y (x 2 ,y 2 )

x = \mathbf{\frac{x_2 + x_1}{2}}

y = \mathbf{\frac{y_2 + y_1}{2}}

Usando esta fórmula, obtenemos

(2, -3) =  \frac{(x+1)}{2} , \frac{(y+4)}{2}

\frac{(x+1)}{2}  = 2 y  \frac{(y+4)}{2}  = -3

x + 1 = 4 y y + 4 = -6

x = 3 y y = -10

Las coordenadas de A (3,-10).

Pregunta 8. Si A y B son (– 2, – 2) y (2, – 4), respectivamente, encuentre las coordenadas de P tales que AP = 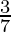 \frac{3}{7}  AB y P se encuentra en el segmento de línea AB.

Solución:

Las coordenadas del punto A y B son (-2,-2) y (2,-4) respectivamente. Como AP =  \mathbf{\frac{3}{7}}  AB

\frac{AB}{AP}  =  \frac{7}{3} ——–(1)

restar 1 de ambos lados,

\frac{AB}{AP}  – 1 =  \frac{7}{3}  – 1

\frac{AB-AP}{AP} = \frac{7-3}{3}

\frac{BP}{AP} = \frac{4}{3}

Por lo tanto, AP: PB = 3:4

El punto P divide el segmento de recta AB en la razón 3:4.

Aquí,

m = 3 y n = 4

(x 1 ,y 1 ) = (-2,-2)

(x 2 ,y 2 ) = (2,-4)

entonces, la coordenada x de P será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(3*2 + 4*(-2))}{3+4}

x = \frac{-2}{7}

y ahora, la coordenada y de P será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(3*(-4) + 4*(-2))}{ 3+4}

y = \frac{-20}{7}

Por lo tanto, la coordenada de P(x,y) es  (\mathbf{\frac{-2}{7}} , \mathbf{\frac{-20}{7}}) .

Pregunta 9. Encuentra las coordenadas de los puntos que dividen el segmento de recta que une A(– 2, 2) y B(2, 8) en cuatro partes iguales.

Solución:

Segmento de recta que une A(– 2, 2) y B(2, 8) dividido en cuatro partes iguales.

  • Podemos decir que Q es el punto medio de AB

Aquí,

m = 1 y n = 1

(x 1 , y 1 ) = (-2,2)

(x2 , y2 ) = (2,8)

entonces, la coordenada x de Q será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(1*2 + 1*(-2))}{ 1+1}

x = 0

y ahora, la coordenada y de Q será,

y = \mathbf{\frac{mi_2 + ny_1}{m+n}}

y = \frac{(1*8 + 1*2)}{ 1+1}

y = 5

Por tanto, la coordenada de Q es (0,5)………………………………..(1)

  • Podemos decir que P es el punto medio de AQ

Aquí,

m = 1 y n = 1

(x 1 , y 1 ) = (-2,2)

(x 2 , y 2 ) = (0,5)

entonces, la coordenada x de P será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(1*0 + 1*(-2))}{ 1+1}

x = -1

y ahora, la coordenada y de P será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(1*5 + 1*2)}{1+1}

y = \frac{7}{2}

Por lo tanto, la coordenada de P es (-1, \mathbf{\frac{7}{2}} )………………………………..(2)

  • Ahora, podemos decir que R es el punto medio de BQ

Aquí,

m = 1 y n = 1

(x 1 , y 1 ) = (2,8)

(x 2 , y 2 ) = (0,5)

entonces, la coordenada x de R será,

x = \mathbf{\frac{mx_2 + nx_1}{m+n}}

x = \frac{(1*0 + 1*2)}{1+1}

X = 1

y ahora, la coordenada y de R será,

y = \mathbf{\frac{my_2 + ny_1}{m+n}}

y = \frac{(1*5 + 1*8)}{ 1+1}

y = \frac{13}{2}

Por lo tanto, la coordenada de R es (1, \mathbf{\frac{13}{2}} )………………………………..(3)

De (1), (2) y (3) concluimos que

Tres puntos entre A y B son (-1, \mathbf{\frac{7}{2}} ), (0,5) y (1, \mathbf{\frac{13}{2}} ).

Pregunta 10. Encuentra el área de un rombo si sus vértices son (3, 0), (4, 5), (– 1, 4) y (– 2, – 1) tomados en orden. [Sugerencia: Área de un rombo = ½ (producto de sus diagonales)]

Solución:

Sean P(3, 0), Q (4, 5), R(– 1, 4) y S (– 2, – 1) los vértices de un rombo PQRS.

Área de un rombo = ½ (producto de sus diagonales)

Longitud de la diagonal 1 (PR) = √((3-(-1)) 2 +(0-4) 2 ) = √32 = 4√2 unidades

Longitud de la diagonal 2 (QS) = √((4-(-2)) 2 +(5-(-1)) 2 ) = √72 = 6√2 unidades

Área de un rombo = ½ × 4√2 × 6√2

Área de un rombo = 24 unidades cuadradas

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *