Soluciones NCERT Clase 10 – Capítulo 7 Geometría de coordenadas – Ejercicio 7.4

Posted on by Rudeus Greyrat

Pregunta 1. Determina la razón en la que la recta 2x + y – 4 = 0 divide el segmento de recta que une los puntos A(2, -2) y B(3, 7).

Dado: 2x + y – 4 = 0 la recta divide el segmento de recta que une los puntos A(2, -2) y B(3, 7)

Hallar: Razón en que la recta dada divide al segmento de recta que une los puntos A y B

Entonces, las coordenadas de C son [\frac{m_1x_2+m_2x_1}{m1+m2},\frac{m_1y_2+m_2y_1}{m1+m2}]

Ahora, consideremos que la relación es k: 1

= [\frac{k(3)+1(2)}{k+1},\frac{k(7)+(-2)}{k+1}]

= (\frac{3k+2}{k+1}\frac{7k}{k+1})

Pero c se encuentra en 2x+y-4=0

Asi que, 

2 [\frac{3k+2}{k+1}+[\frac{7k}{k+1}] – 4 = 0

\frac{6k+4}{k+1}+\frac{7k-2}{k+1}-\frac{4}{2}=0

\frac{6k+4+7k-2-4(k+1)}{k+1}=\frac{0}{1}

\frac{6k+4+7k-2-4k-4}{13k-4k-2}=\frac{0}{0}

9k = 2

k/1 = 2/9

Por lo tanto, la relación es 2:9.

Pregunta 2. Encuentra una relación entre x e y, si los puntos (x, y), (1, 2) y (7, 0) son colineales.

Encontrar: Aquí, tenemos que encontrar una relación entre x e y, si los puntos (x, y), (1, 2) y (7, 0) son colineales.

Si los puntos dados son colineales, entonces el área del triángulo es 0 (creado usando estos puntos).

Asi que, 

Área del triángulo = 1/2[x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )] = 0

=> x(2 – 0) + 1(0 – y) + 7(y – 2) = 0

=> x(2)+ 1(-y) + 7y – 14 = 0

=> 2x – y + 7y – 14 = 0

=> 2x + 6y – 14 = 0

Al dividir por 2 en ambos lados, obtenemos  

x + 3y – 7 = 0

Por lo tanto, la relación requerida es x + 3y – 7 = 0 

Pregunta 3. Encuentra el centro de un círculo que pasa por los puntos (6, -6), (3, -7) y (3, 3).

Consideremos el punto A(6, -6), B(3, -7), y C(3, 3) y P(x, y) es el centro del círculo.

Entonces, AP = BP = CP (los radios son iguales)

Ahora primero tomamos

AP = PA

√((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ) = √((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 )

(x – 6) 2 + (y + 6) 2 = (x – 3) 2 + (y + 7) 2

x2 + 36 – 12x + y2 + 36 + 12y = x2 + 9 – 6x + y2 + 49 + 14y

36 – 12x + 36 + 12y = 9 – 6x + 49 + 14y

-12x + bx + 12y – 14y + 72 – 58 = 0

-6x – 2y + 14 = 0

6x + 2y – 14 = 0

Al dividir por 2 en ambos lados, obtenemos

3x + y – 7 = 0 -(1) 

Ahora, tomamos 

BP = CP

√((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ) = √((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 )

(x – 3) 2 + (y + 7) 2 = (x – 3) 2 + (y – 3) 2

y 2 + 7 2 + 2(y)(7) = y 2 + 3 2 – 2(y)(3)

49 + 14 años = 9 – 6 años

14 años + 6 años = 9 – 49

20 años = -40

y = -40/20

y = -2

Ahora, al poner el valor de y = -2 en la ecuación (1), obtenemos

3x – 2 – 7 = 0

3x – 9 = 0

3x = 9

X = 9/3 = 3

Por tanto, el centro P(x, y) = (3, -2)  

Pregunta 4. Los dos vértices opuestos de un cuadrado son (-1, 2) y (3, 2). Encuentra las coordenadas de los otros dos vértices.

Consideremos que ABDC es un cuadrado, y sus dos vértices opuestos son A(-1, 2) y C(3, 2). 

Deje que el punto O interseque la línea AC y BD. 

Ahora, primero encontraremos la coordenada del punto O(x, y)

Como sabemos que O es el punto medio de la línea AC,

x = (3 – 1)/2 = 1 

y = (2 + 2)/2 = 2 

Entonces, la coordenada del punto O es (1, 2)

Ahora encontraremos el lado del Cuadrado.

CA = √((3+ 1) 2 + (2– 2) 2 ) 

CA = √16 = 4

Entonces, en el triángulo ACD, usando el teorema de la hipotenusa, obtenemos

a = 2√2

Entonces, cada lado del cuadrado es 2√2

Para la coordenada de D: 

Supongamos que la coordenada de D es (x 1 , y 1 ).

Como sabemos que los lados de los cuadrados son iguales

entonces AD = CD

√((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ) = √((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 )

√(x 1 + 1) 2 + (y 1 – 2) 2 = √(x 1 – 3) 2 + (y 1 – 2) 2

(x 1 + 1) 2 + (y 1 – 2) 2 = (x 1 – 3) 2 + (y 1 – 2) 2

(x 1 + 1) 2 = (x 1 – 3) 2

x 1 2 + 1 + 2x 1 = x 1 2 + 9 – 6x 1

1 + 2x 1 = 9 – 6x 1

2x 1 + 6x 1 = 9 – 1

8×1 = 8

× 1 = 1

Ahora, CD 2 = ((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 )

8 = (x 1 – 3) 2 + (y 1 – 2) 2

8 = x 1 2 + 9 – 6x 1 + y 1 2 + 4 – 4y 1

y 1 – 2 = 2

y 1 = 4

Entonces la coordenada de D es (1, 4)

Para la coordenada de B:

Sea B(x 2 , y 2 ) y como sabemos que DBO es un segmento de recta, entonces, 

1 = x 2 + 1/2 

× 2 = 1

2 = y 2 + 4/2 

y 2 = 0

Entonces la coordenada de B = (1, 0)

Pregunta 5. A los estudiantes de la clase X de la escuela en krishnagar se les ha asignado un terreno rectangular para su actividad de jardinería. Los árboles jóvenes de Gulmohar se plantan en el límite a una distancia de 1 m entre sí. Hay césped triangular en la parcela como se muestra en la figura. Los estudiantes deben sembrar semillas de plantas con flores en el área restante de la parcela.

(i) Tomando A como origen, encuentre las coordenadas de los vértices del triángulo.

(ii) ¿Cuáles serán las coordenadas de los vértices de ∆PQR, si C es el origen?

Además, calcula las áreas de los triángulos en estos casos. ¿Qué observas?

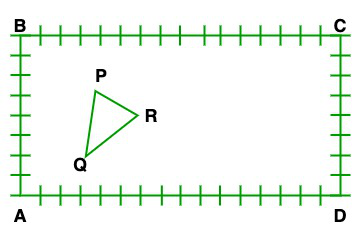
(i) Ahora tomando A como origen las coordenadas de los vértices del triángulo son 

PAG = (4, 6)

Q = (3, 2)

R = (6, 5)

(ii) Ahora tomando C como origen las coordenadas de los vértices del triángulo son

PAG = (12, 2)

Q = (13, 6)

R = (10, 3) 

Encontrar el área del triángulo, cuando A como origen las coordenadas de los vértices

del triángulo son P(4, 6), Q(3, 2) y R(6, 5)

Area1 = 1/2[x 1 (y 2 – y 3 ) + x2(y 3 – y 1 ) + x 3 (y 1 – y 2 )]

= [4(2 – 5) + 3(5 – 6) + 6(6 – 2)]/2

= [-12 – 3 + 24]/2

= [-15 + 24]/2

= 9/2 unidad cuadrada

Encontrar el área del triángulo, cuando C como origen las coordenadas de los vértices

 del triángulo son P(12, 2), Q(13, 6) y R(10, 3)

Área2 = [12(6 – 3) + 13(3 – 2) + 10(2 – 6)]/2

= [12(3) + 13(1) + 10(-4)]/2

= [36 + 13 – 40]/2

= [49 – 40]/2

= 9/2 unidad cuadrada

Entonces, aquí observamos que el Area1 = Area2

Pregunta 6. Los vértices de un ∆ABC son A (4, 6), B (1, 5) y C (7, 2). Se dibuja una recta que corta los lados AB y AC en D y E respectivamente, tal que AD/AB = AE/AC = 1/4. Calcula el área del ∆ ADE y compárala con el área del ∆ ABC.

Solución:

Dado: AD/AB = AE/AC = 1/4

Para hallar: Área de ∆ADE

Dado que D y E dividen a AB y AC es la misma proporción 1:4 entonces DE||BC -(Usando el teorema 6.2)

Ahora, en ∆ADE y ∆ABC

∠A = ∠A -(Ángulo común)

∠D = ∠B -(Ángulos correspondientes)

∴∆ADE~∆ABC -(similitud AA)

ar.(ADE)/ar.(ABC) = (AD/AB) 2 = 1/16          

Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )]

= [4(5 – 2) + 1(2 – 6) + 7(6 – 5)]/2

= [4(3) + 1(-4) + 7(1)]/2

= [12 – 4 + 7]/2

= [19 – 4]/2         

= 15/2 unidad cuadrada

ar.(ADE)/ar.(ABC) = -(1/10)

ar.(ADE) = (1/16) × ar.(ABC)

ar.(ADE) = (1/16) × (15/2) = 15/32 unidad cuadrada

Entonces, obtenemos

ar.(ADE):ar.(ABC) = 1:16

Pregunta 7. Sean A(4, 2), B(6, 5) y C(1, 4) los vértices de ∆ABC.

(i) La mediana desde A metros BC en D. Encuentre las coordenadas del punto D.

(ii) Encuentre las coordenadas del punto P en el AD, tales que AP: PD = 2: 1.

(iii) Encuentre las coordenadas de los puntos Q y R en las medianas BE y CF respectivamente, tales que BQ: QE = 2: 1 y CR: RF = 2: 1.

(iv) ¿Qué observa?

[Nota: los puntos que son comunes a las tres medianas se denomina centroide y este punto divide cada mediana en la proporción 2: 1]

(v) Si A(x1, y1), B(x2, y2) y C(x3, y3) son los vértices de ∆ABC, encuentre las coordenadas del centroide de los triángulos.

Solución:

Dado: Los vértices de ∆ABC son A(4, 2), B(6, 5) y C(1, 4)

(i) Coordenadas de D = Punto medio de BC

= [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]

= [\frac{6+1}{2},\frac{5+4}{2}]

= [7/2, 9/2]

= (3.5, 4.5)

(ii) Coordenadas de P =[\frac{m_1x_1+m_2x_2}{2},\frac{m_1y_1+m_2y_2}{2}]

= [\frac{(3.5)2+1(4)}{2+1},\frac{(4.5)2+1(2)}{2+1}]

= [\frac{7+4}{3},\frac{9+2}{3}]

= [11/3, 11/3]

(iii) Coordenadas E = Punto medio de AC 

= [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]

= [\frac{4+1}{2},\frac{2+4}{2}]

= (2.5, 3)

(iv) Observamos que los puntos P, Q y R coinciden, es decir, las medianas de AD, BE y 

concurrente en el punto [11/3, 11/3]. Este punto se conoce como el baricentro del triángulo.

(v) Como AD es la mediana, D es el punto medio de BC

Entonces las coordenadas de D:

= [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]

= [\frac{x_2+x_3}{2},\frac{y_2+y_3}{2}]

Coordenadas de G:

= [\frac{x_2m_1+m_2x_1 }{m_1+m_2},\frac{y_2m_1+y_1m_12}{m_1+m_2}]                                   

Pregunta 8. ABCD es un rectángulo formado por los puntos A(-1, -1), B(-1, 4), C(5, 4) y D(5, -1), P, Q, R y S son los puntos medios de AB, BC, CD y DA respectivamente. ¿El cuadrilátero PQRS es un cuadrado? ¿un rectángulo? o un rombo? Justifica tu respuesta.

Solución:

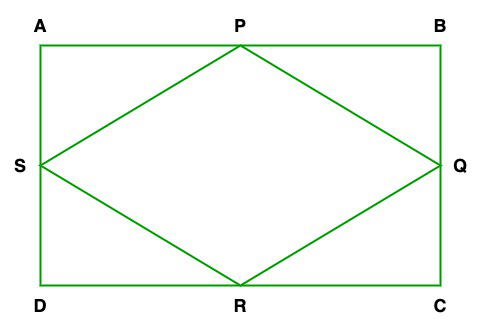
Dado: Los puntos A(-1, -1), B(-1, 4), C(5, 4) y D(5, -1) y P, Q, R y S son los puntos medios de AB, BC, CD y DA 

Asi que, 

P(\frac{-1-1}{2},\frac{-1+1}{2})  = (-2/2, -1, 3/2)

Q(\frac{-1+5}{2},\frac{4+4}{3})  = (4/2, 8/2) = (2, 4)

R(\frac{5+5}{2},\frac{4-1}{2})  = (10/2, 8/2) = (5, 3/2)

S(\frac{5-1}{2},\frac{-1-1}{2})  = (4/2, -2/2) = (2, 1)

Entonces, la longitud de PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

=\sqrt{(2+1)^2+(4-\frac{3}{2})^2}

=\sqrt{(3)^2+(\frac{5}{2})^2}

=\sqrt{9+\frac{25}{2}}

= √(61/4)

El largo de QR=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

=\sqrt{(3)^2+(\frac{-5}{2})^2}   

=\sqrt{9+\frac{25}{4}}

= √(61/4)

El largo de RS=\sqrt{(2-5)^2+(21-\frac{3}{2})^2}

=\sqrt{(-3)^2+(\frac{-5}{2})^2}

=\sqrt{9+\frac{25}{4}}

= √(61/4)

El largo de SP=\sqrt{(-1-2)^2+(\frac{3}{2}+1)^2}

=\sqrt{(-3)^2+(\frac{5}{2})^2}

=\sqrt{9+\frac{25}{4}}

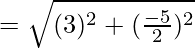
= √(61/4)

La longitud de la diagonal QS=\sqrt{(2-2)^2+(-1-4)^2}

 =\sqrt{(0)^2+(-5)^2}

= √25 = 5 

La longitud de la diagonal PR=\sqrt{(5+1)^2+(\frac{3}{2}\frac{-3}{2})^2}

=\sqrt{(6)^2+(0)^2}   

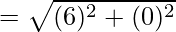
= √36 = 6                 

Por lo tanto, todos los cuatro lados son iguales (es decir, PQ = QR = RS = SP) pero las diagonales son 

no iguales entre sí (es decir, QS ≠ PR). 

Por lo tanto, dado el cuadrilátero PQRS es un rombo.  

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *