Capítulo 9 Algunas aplicaciones de la trigonometría – Ejercicio 9.1 | Serie 1
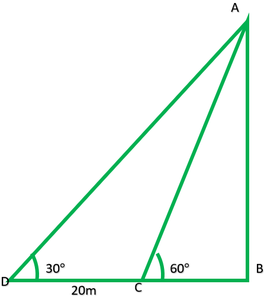
Pregunta 11. Una torre de televisión se encuentra verticalmente en la orilla de un canal. Desde un punto en la otra orilla directamente opuesto a la torre, el ángulo de elevación de la parte superior de la torre es de 60°. Desde otro punto a 20 m de este punto en la línea que une este punto con el pie de la torre, el ángulo de elevación de la parte superior de la torre es de 30° (ver Fig.). Encuentra la altura de la torre y el ancho del canal.
Solución:
En la figura: AB = torre = ?
CB = canal = ?
En rt. ∆ABC,
tan60° =
h/x = √3
h = √3 x -(1)
En rt. ∆ABD
= bronceado 30°
= 1/√3
h = (x + 20)/√3 -(2)
De (1) y (2)
√3/1 = (x + 20)/√3
3x = x + 20
3x – x = 20
2x = 20
X = 20/2
X = 10
El ancho del canal es de 10 m.
Poner el valor de x en la ecuación 1
h = √3 x
= 1.732(10)
= 17,32
Altura de la torre 17,32m.
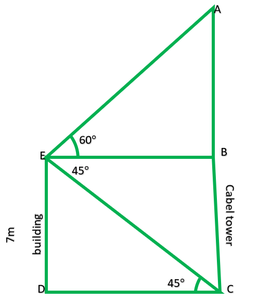
Pregunta 12. Desde lo alto de un edificio de 7 m de altura, el ángulo de elevación de la parte superior de una torre de cable es de 60° y el ángulo de depresión de su pie es de 45°. Determinar la altura de la torre.
Solución:
En la figura: ED = edificio = 7m
CA = torre de cable = ?
En rt ∆EDC,
= tan45°
7/x = 1/1
CC = 7
Ahora, EB = DC = 7m
En rt. ∆ABE,
= tan60°
AB/7 = √3/1
Altura de la torre = AC = AB + BC
7√3 + 7
= 7(√3 + 1)
= 7(1.732 + 1)
= 7(2.732)
Altura de la torre de cable = 19.125m
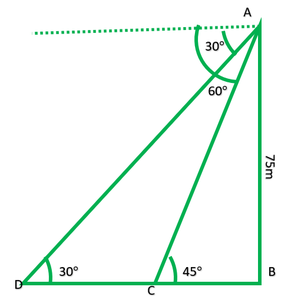
Pregunta 13. Como se observa desde lo alto de un faro de 75 m de altura desde el nivel del mar, los ángulos de depresión de dos barcos son 30° y 45°. Si un barco está exactamente detrás del otro en el mismo lado del faro, encuentra la distancia entre los dos barcos.
Solución:
En la Fig:
AB = faro = 75m
D y C son dos barcos
CC = ?
En rt. ∆ABD,
= tan30°
75/BD = 1/√3
BD = 75√3
En rt. ∆ABC
= tan45°
75/AC = 1/1
BC = 75
CC = BD – BC
= 75√3 – 75
75(√3 – 1)
75(1.372 – 1)
34.900
Por lo tanto, la distancia entre dos ovejas es 34.900
Pregunta 14. Una niña de 1,2 m de altura ve un globo que se mueve con el viento en una línea horizontal a una altura de 88,2 m del suelo. La altura de 88,2 m desde el suelo. El ángulo de elevación del globo desde los ojos de la niña en cualquier instante es de 60°. Después de un tiempo, el ángulo de elevación se reduce a 30° (ver Fig.). Encuentre la distancia recorrida por el globo durante el intervalo.
Solución:
En la figura: AB = AC – BC
= 88,2 – 1,2
= 81m
En rt. ∆ABE
= 87/EB = tan30°
87/EB = 1/√3
EB = 87√3
En rt. ∆FDE
= tan60°
√3 DE = 87
DE = 87/√3
DB = DB – ED
87√3 – 87/√3
87(√3 – 1/√3)
= 87(3 – 1/√3)
= 87(2/√3) = 174/√3 * √3/√3
= 174 * √3/3 = 58√3
58 * 1.732 = 100.456m
La distancia recorrida por el globo es 100.456m
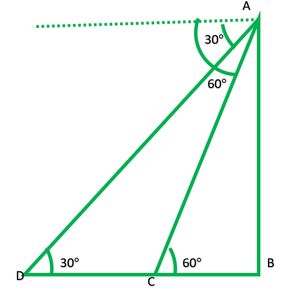
Pregunta 15. Una carretera recta conduce al pie de una torre. Un hombre parado en lo alto de la torre observa un automóvil con un ángulo de depresión de 30°, que se acerca al pie de la torre con rapidez uniforme. Seis segundos después, se encuentra que el ángulo de depresión del automóvil es de 60°. Encuentre el tiempo que tarda el automóvil en llegar al pie de la torre desde este punto.
Solución:
En la figura: AB es torre
En rt. ∆ABD
= tan30°
= 1/√3
BD = √3 AB -(1)
En rt. ∆ABC
= tan60°
BC = AB/√3 -(2)
CC = BD – BC
= √3 AB – AB/√3
AB(3 – 1/√3)
CD = 2AB/√3
S1 = S2
\frac{D1}{T1} = \frac{D2}{T2}
2/√3AB/6 = AB/√3/t
2t = 6
t = 6/2
t = 3 seg
Pregunta 16. Los ángulos de elevación de la parte superior de una torre desde dos puntos a una distancia de 4 m y 9 m de la base de la torre y en la misma línea recta con ella son complementarios. Demostrar que la altura de la torre es de 6 m.
Solución:
En la figura: AB es torre
Para probar: AB = 6m
Dado: BC = 4m DB = 9m
en ∆ABC
= tanθ
AB/4 = tanθ -(1)
en ∆ABD
= bronceado (90°-θ)
AB/9 = 1/ tanθ
9/AB = tanθ -(2)
De (1) y (2)
AB/4 = 9/AB
AB2 = 36
AB = √36
AB = √(6 * 6)
AB = 6m
La altura de la torre es de 6 m.

Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA