Soluciones NCERT de clase 8 – Capítulo 6 Cuadrados y raíces cuadradas – Ejercicio 6.4

Pregunta 1. Encuentra la raíz cuadrada de cada uno de los siguientes números por el método de división.

(yo) 2304

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{23}$ $\overline{04}$

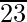
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 23

Divide y obtén el resto.

Aquí tenemos 7

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, es 04

Así que ahora el nuevo dividendo es 704.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 88 × 8 = 704.

Así que elegimos el nuevo dígito como 8.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √2304 = 48

(ii) 4489

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{44}$ $\overline{89}$

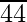
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 44

Divide y obtén el resto.

Aquí tenemos 8

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, su 89

Así que ahora el nuevo dividendo es 889.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 127 × 7 = 889.

Así que elegimos el nuevo dígito como 7.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √4489 = 67

(iii) 3481

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{34}$ $\overline{81}$

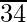
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 34

Divide y obtén el resto.

Aquí tenemos 9

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, su 81

Así que ahora el nuevo dividendo es 981.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 109 × 9 = 981.

Así que elegimos el nuevo dígito como 9.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √3481 = 59

(iv) 529

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{5}$ $\overline{29}$

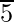
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 5

Divide y obtén el resto.

Aquí tenemos 1

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, es 29

Así que ahora el nuevo dividendo es 129.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 23 × 3 = 129.

Así que elegimos el nuevo dígito como 3.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √529 = 23

(v) 3249

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{32}$ $\overline{49}$

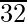
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 32

Divide y obtén el resto.

Aquí tenemos 7

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, sus 49

Así que ahora el nuevo dividendo es 749.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 107 × 7 = 749.

Así que elegimos el nuevo dígito como 7.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √3249 = 57

(vi) 1369

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{13}$ $\overline{69}$

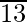
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 13

Divide y obtén el resto.

Aquí tenemos 4

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, su 69

Así que ahora el nuevo dividendo es 469.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 37 × 7 = 469.

Así que elegimos el nuevo dígito como 7.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √1369 = 37

(vii) 5776

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{57}$ $\overline{76}$

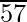
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 57

Divide y obtén el resto.

Aquí tenemos 8

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, sus 76

Así que ahora el nuevo dividendo es 876.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 146 × 6 = 876.

Así que elegimos el nuevo dígito como 6.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √5776 = 76

(viii) 7921

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{79}$ $\overline{21}$

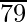
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 79

Divide y obtén el resto.

Aquí tenemos 15

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, es 21

Así que ahora el nuevo dividendo es 1521.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 169 × 9 = 1521.

Así que elegimos el nuevo dígito como 9.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √7921 = 89

(ix) 576

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{5}$ $\overline{76}$

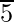
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 5

Divide y obtén el resto.

Aquí tenemos 1

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, sus 76

Así que ahora el nuevo dividendo es 176.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 44 × 4 = 176.

Así que elegimos el nuevo dígito como 4.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √576 = 24

(x) 1024

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{10}$ $\overline{24}$

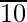
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 10

Divide y obtén el resto.

Aquí tenemos 1

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

aquí, son 24

Así que ahora el nuevo dividendo es 124.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 62 × 2 = 124.

Así que elegimos el nuevo dígito como 2.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √1024 = 32

(xi) 3136

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{31}$ $\overline{36}$

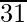
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 31

Divide y obtén el resto.

Aquí tenemos 6

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, sus 36

Así que ahora el nuevo dividendo es 636.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 106 × 6 = 636.

Así que elegimos el nuevo dígito como 6.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √3136 = 56

(xii) 900

Solución:

Paso 1 : coloque una barra sobre cada par de dígitos a partir del dígito en el lugar de uno. Si el número de dígitos es impar, entonces el único dígito más a la izquierda también tendrá una barra.

Así tenemos, $\overline{9}$ $\overline{00}$

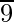
Paso 2 : encuentre el número más grande cuyo cuadrado sea menor o igual que el número debajo de la barra del extremo izquierdo. Toma este número como divisor y el cociente con el número debajo de la barra del extremo izquierdo como dividendo.

Aquí tenemos 9

Divide y obtén el resto.

Aquí, obtenemos 0

Paso 3 : baja el número restante debajo de la siguiente barra a la derecha del resto.

Aquí, es 0

Así que ahora el nuevo dividendo es 000.

Paso 4 : Duplique el cociente e ingréselo con un espacio en blanco a su derecha.

Paso 5 : Adivina el dígito más grande posible para llenar el espacio en blanco que también se convertirá en el nuevo dígito en el cociente, de modo que cuando el nuevo divisor se multiplique por el nuevo cociente, el producto sea menor o igual que el dividendo.

En este caso 60 × 0 = 000.

Así que elegimos el nuevo dígito como 0.

Consigue el resto.

Paso 6 : Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √900 = 30

Pregunta 2. Encuentra el número de dígitos en la raíz cuadrada de cada uno de los siguientes números (sin ningún cálculo).

Si n es el número de dígitos en un número cuadrado entonces

Número de dígitos en la raíz cuadrada = $\frac {n}{2}$ si n es par

y, $\frac{n+1}{2}$ si n es impar .

(yo) 64

Solución:

Aquí, n = 2, que es par

Entonces, el número de dígitos en la raíz cuadrada es = $\frac {n}{2}$

= $\frac {2}{2}$

= 1

(ii) 144

Solución:

Aquí, n = 3, que es impar

Entonces, el número de dígitos en la raíz cuadrada es = $\frac {n+1}{2}$

= $\frac {4}{2}$

= 2

(iii) 4489

Solución:

Aquí, n = 4, que es par

Entonces, el número de dígitos en la raíz cuadrada es = $\frac {n}{2}$

= $\frac {4}{2}$

= 2

(iv) 27225

Solución:

Aquí, n = 5, que es impar

Entonces, el número de dígitos en la raíz cuadrada es = $\frac{n+1}{2}$

= $\frac{6}{2}$

= 3

(v) 390625

Solución:

Aquí, n = 6, que es par

Entonces, el número de dígitos en la raíz cuadrada es = $\frac{n}{2}$

= $\frac{6}{2}$

= 3

Pregunta 3. Encuentra la raíz cuadrada de los siguientes números decimales.

(yo) 2.56

Solución:

Para encontrar la raíz cuadrada de un número decimal ponemos barras en la parte integral del número de la manera habitual. Y coloca barras en la parte decimal de cada par de dígitos comenzando con el primer lugar decimal.

Obtenemos $\overline{2}.\overline{56}$

Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √2,56 = 1,6

(ii) 7.29

Solución:

Para encontrar la raíz cuadrada de un número decimal ponemos barras en la parte integral del número de la manera habitual. Y coloca barras en la parte decimal de cada par de dígitos comenzando con el primer lugar decimal.

Obtenemos $\overline{7}.\overline{29}$

Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √7.29 = 2.7

(iii) 51,84

Solución:

Para encontrar la raíz cuadrada de un número decimal ponemos barras en la parte integral del número de la manera habitual. Y coloca barras en la parte decimal de cada par de dígitos comenzando con el primer lugar decimal.

Obtenemos $\overline{51}.\overline{84}$

Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √51,84 = 7,2

(iv) 42,25

Solución:

Para encontrar la raíz cuadrada de un número decimal ponemos barras en la parte integral del número de la manera habitual. Y coloca barras en la parte decimal de cada par de dígitos comenzando con el primer lugar decimal.

Obtenemos $\overline{42}.\overline{25}$

Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √42,25 = 6,5

(v) 31.36

Solución:

Para encontrar la raíz cuadrada de un número decimal ponemos barras en la parte integral del número de la manera habitual. Y coloca barras en la parte decimal de cada par de dígitos comenzando con el primer lugar decimal.

Obtenemos $\overline{31}.\overline{36}$

Dado que el resto es 0 y no quedan dígitos en el número dado.

Por lo tanto, √31,36 = 5,6

Pregunta 4. Encuentra el número mínimo que se debe restar de cada uno de los siguientes números para obtener un cuadrado perfecto. Halla también la raíz cuadrada del cuadrado perfecto así obtenido.

Aquí, el resto es el número mínimo que se requiere restar del número dado para obtener un cuadrado perfecto.

(yo) 402

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí el resto es 2

2 es el número mínimo requerido para ser restado de 402 para obtener un cuadrado perfecto

Nuevo número = 402 – 2 = 400

Por lo tanto, √400 = 20

(ii) 1989

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí el resto es 53

53 es el número mínimo requerido para ser restado de 1989.

Nuevo número = 1989 – 53 = 1936

Así, √1936 = 44

(iii) 3250

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí el resto es 1

1 es el número mínimo que se requiere restar de 3250 para obtener un cuadrado perfecto.

Nuevo número = 3250 – 1 = 3249

Por lo tanto, √3249 = 57

(iv) 825

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí, el resto es 41

41 es el número mínimo requerido que se puede restar de 825 para obtener un cuadrado perfecto.

Nuevo número = 825 – 41 = 784

Por lo tanto, √784 = 28

(v) 4000

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí, el resto es 31

31 es el número mínimo requerido que debe restarse de 4000 para obtener un cuadrado perfecto.

Nuevo número = 4000 – 31 = 3969

Por lo tanto, √3969 = 63

Pregunta 5. Encuentra el número mínimo que se debe sumar a cada uno de los siguientes números para obtener un cuadrado perfecto. Halla también la raíz cuadrada del cuadrado perfecto así obtenido.

(yo) 525

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí el resto es 41

Representa que 22 ² es menor que 525.

El siguiente número es 23,

Donde, 23 ² = 529

Por lo tanto, el número a sumar = 529 – 525 = 4

Nuevo número = 525+4 = 529

Por lo tanto, √529 = 23

(ii) 1750

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí el resto es 69

Representa que 41 ² es menor que en 1750.

el siguiente numero es 42

Donde, 42 ² = 1764

Por lo tanto, número a sumar a 1750 = 1764 – 1750 = 14

Nuevo número = 1750 + 14 = 1764

√1764 = 42

(iii) 252

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí el resto es 27.

Representa que 15 ² es menor que 252.

el siguiente numero es 16

Donde,16 ² = 256

Por lo tanto, el número que se suma a 252 = 256 – 252 = 4

Nuevo número = 252 + 4 = 256

y √256 = 16

(iv) 1825

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

El resto es 61.

Representa que 42 ² es menor que en 1825.

el proximo numero es 43

Donde, 43 ² = 1849

Por lo tanto, el número que se sumará a 1825 = 1849 – 1825 = 24

Nuevo número = 1825 + 24 = 1849

y √1849 = 43

(v) 6412

Solución:

Siguiendo todos los pasos para obtener la raíz cuadrada, obtenemos

Aquí, el resto es 12.

Representa que 80 ² es menor que en 6412.

el siguiente numero es 81

Donde, 81 ² = 6561

Por lo tanto, el número a sumar = 6561 – 6412 = 149

Nuevo número = 6412 + 149 = 6561

y √6561 = 81

Pregunta 6. Encuentra la longitud del lado de un cuadrado cuya área es 441 m ² .

Solución:

Sea el lado del cuadrado x m.

Área del cuadrado = x ²

De acuerdo con la pregunta dada,

× ² = 441

x = √441

Por lo tanto, el lado del cuadrado es de 21 m.

Pregunta 7. En un triángulo rectángulo ABC, ∠B = 90°.

(a) Si AB = 6 cm, BC = 8 cm, encuentre AC

Solución:

En el triángulo rectángulo ABC

AC ² = AB ² + BC ² [ Por el teorema de Pitágoras ]

CA ² = 6 ² + 8 ²

CA ² = 100

CA = √100

CA = 10 cm

(b) Si AC = 13 cm, BC = 5 cm, encuentre AB

Solución:

En el triángulo rectángulo ABC

AC ² = AB ² + BC ² [Por el teorema de Pitágoras]

13 ² = AB ² + 5 ²

AB ² = 13 ² – 5 ²

AB2 ⁼ (13+5) (13-5)

AB2 ⁼ 18 × 8

AB2 ⁼ 144

AB = √144

AB = 12 cm

Pregunta 8. Un jardinero tiene 1000 plantas. Quiere plantarlos de tal manera que el número de filas y el número de columnas permanezcan iguales. Encuentra el número mínimo de plantas que necesita más para esto.

Solución:

Sea x el número de filas y columnas.

Número total de plantas = x ²

× ² = 1000

x = √1000

Aquí el resto es 39

Entonces el 31 ² es menor que 1000.

el proximo numero es 32

Donde, 32 ² = 1024

Por lo tanto, el número a sumar = 1024 – 1000 = 24

Por lo tanto, el número mínimo de plantas requeridas por él = 24.

Pregunta 9. Hay 500 niños en una escuela. Para un ejercicio PT, deben colocarse de tal manera que el número de filas sea igual al número de columnas. ¿Cuántos niños quedarían fuera en este arreglo?

Solución:

Sea x el número de filas y columnas.

Número total de plantas = x ²

× ² = 500

x = √500

Aquí el resto es 16

Número nuevo 500 – 16 = 484

y, √484 = 22

Por lo tanto, 16 estudiantes quedarán fuera de este arreglo.

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la raíz cuadrada de cada uno de los siguientes números por el método de división.

(yo) 2304

Solución:

(ii) 4489

(iii) 3481

(iv) 529

(v) 3249

(vi) 1369

(vii) 5776

(viii) 7921

(ix) 576

(x) 1024

(xi) 3136

(xii) 900

Pregunta 2. Encuentra el número de dígitos en la raíz cuadrada de cada uno de los siguientes números (sin ningún cálculo).

(yo) 64

(ii) 144

(iii) 4489

(iv) 27225

(v) 390625

Pregunta 3. Encuentra la raíz cuadrada de los siguientes números decimales.

(yo) 2.56

(ii) 7.29

(iii) 51,84

(iv) 42,25

(v) 31.36

Pregunta 4. Encuentra el número mínimo que se debe restar de cada uno de los siguientes números para obtener un cuadrado perfecto. Halla también la raíz cuadrada del cuadrado perfecto así obtenido.

(yo) 402

(ii) 1989

(iii) 3250

(iv) 825

(v) 4000

Pregunta 5. Encuentra el número mínimo que se debe sumar a cada uno de los siguientes números para obtener un cuadrado perfecto. Halla también la raíz cuadrada del cuadrado perfecto así obtenido.

(yo) 525

(ii) 1750

(iii) 252

(iv) 1825

(v) 6412

Pregunta 6. Encuentra la longitud del lado de un cuadrado cuya área es 441 m 2 .

Pregunta 7. En un triángulo rectángulo ABC, ∠B = 90°.

(a) Si AB = 6 cm, BC = 8 cm, encuentre AC

(b) Si AC = 13 cm, BC = 5 cm, encuentre AB

Pregunta 8. Un jardinero tiene 1000 plantas. Quiere plantarlos de tal manera que el número de filas y el número de columnas permanezcan iguales. Encuentra el número mínimo de plantas que necesita más para esto.

Pregunta 9. Hay 500 niños en una escuela. Para un ejercicio PT, deben colocarse de tal manera que el número de filas sea igual al número de columnas. ¿Cuántos niños quedarían fuera en este arreglo?

Deja una respuesta Cancelar la respuesta

Pregunta 6. Encuentra la longitud del lado de un cuadrado cuya área es 441 m ² .