Soluciones NCERT de clase 9 – Capítulo 1 Sistema numérico – Ejercicio 1.3

Pregunta 1. Escriba lo siguiente en forma decimal y diga qué tipo de expansión decimal tiene cada uno:

(yo) 36/100

Solución:

En la pregunta dada, obtenemos

Aquí, el resto se convierte en cero.

Por lo tanto, la expansión decimal se convierte en terminación.

36/100 = 0,36

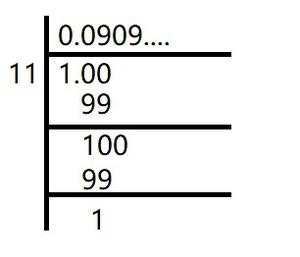
(ii) 1/11

Solución:

En la pregunta dada, obtenemos

Aquí, el resto nunca se convierte en cero y los restos se repiten después de cierta etapa.

Por lo tanto, la expansión decimal es recurrente sin terminación.

1/11 = $0.\overline{09}$

(iii) $4\frac{1}{8}$

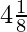
Solución:

Aquí, $4\frac{1}{8} = \frac{33}{8}$

En la pregunta dada, obtenemos

Aquí, el resto se convierte en cero.

Por lo tanto, la expansión decimal se convierte en terminación .

$4\frac{1}{8}$ = 4.125

(iv) 3/13

Solución:

En la pregunta dada, obtenemos

Aquí, el resto nunca se convierte en cero y los restos se repiten después de cierta etapa.

Por lo tanto, la expansión decimal es recurrente sin terminación.

3/13 = $0.\overline{230769}$

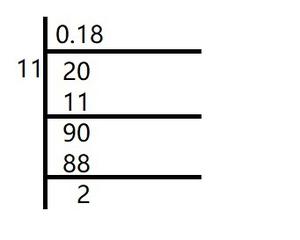
(v) 2/11

Solución:

En la pregunta dada, obtenemos

Aquí, el resto nunca se convierte en cero y los restos se repiten después de cierta etapa.

Por lo tanto, la expansión decimal es recurrente sin terminación.

2/11 = $0.\overline{18}$

(vi) 329/400

Solución:

En la pregunta dada, obtenemos

Aquí, el resto se convierte en cero.

Por lo tanto, la expansión decimal se convierte en terminación .

329/400 = 0,8225

Pregunta 2. Sabes que 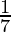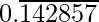$\frac{1}{7}$ = $0.\overline{142857}$ ¿Puedes predecir cuáles son las expansiones decimales de 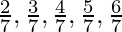$\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$ sin hacer la división larga? ¿Si es así, cómo?

[Sugerencia: estudie los restos mientras encuentra el valor de 1/7 cuidadosamente.]

Solución:

Tal como se da,

$\frac{1}{7} = 0.\overline{142857}$

Asi que,

$\frac{2}{7} = 2(\frac{1}{7}) = 2(0.\overline{142857}) = 0.\overline{285714}$

$\frac{3}{7} = 3(\frac{1}{7}) = 3(0.\overline{142857}) = 0.\overline{428571}$

$\frac{4}{7} = 4(\frac{1}{7}) = 4(0.\overline{142857}) = 0.\overline{571428}$

$\frac{5}{7} = 5(\frac{1}{7}) = 5(0.\overline{142857}) = 0.\overline{714285}$

$\frac{6}{7} = 6(\frac{1}{7}) = 6(0.\overline{142857}) = 0.\overline{857142}$

Pregunta 3: Exprese lo siguiente en la forma p/q, donde p y q son números enteros y q ≠ 0.

(i) 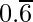$0.\overline{6}$

Solución:

$0.\overline{6}$ = 0.66666……

Tomemos, x = 0.66666……

10x = 6.666….

Asi que,

10x – x = (6,6666…..) – (0,66666……..)

9x = 6

x = 6/9

X = 2/3

Por lo tanto, x tiene la forma p/q, aquí p y q son números enteros y q ≠ 0.

(ii) 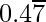$0.4\overline{7}$

Solución:

$0.4\overline{7}$ = 0.4777777……

Tomemos, x = 0.4777777……

10x = 4.77777…….

Asi que,

10x – x = (4.77777…….) – (0.4777777……)

9x = 4,3

9x = 43/10

x = 43/90

Por lo tanto, x tiene la forma p/q, aquí p y q son números enteros y q ≠ 0.

(iii) 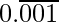$0.\overline{001}$

Solución:

$0.\overline{001}$ = 0.001001001……

Tomemos, x = 0.001001001……

1000x = 1.001001001……

Asi que,

1000x – x = (1.001001001……) – (0.001001001……)

999x = 1

x = 1/999

Por lo tanto, x tiene la forma p/q, aquí p y q son números enteros y q ≠ 0.

Pregunta 4. Expresar 0.99999…. en la forma p/q, ¿Te sorprende tu respuesta? Con tu maestro y compañeros de clase discute por qué la respuesta tiene sentido.

Solución:

Tomemos, x = 0.99999……

10x = 9.99999….

Asi que,

10x – x = (9.99999…..) – (0.99999……..)

9x = 9

X = 1

Como, 0.9999….. simplemente continúa, entonces en algún momento no hay brecha entre 1 y 0.9999….

Podemos observar que 0,999 está demasiado cerca de 1, por lo tanto, 1 se justifica como la respuesta.

Por lo tanto, x tiene la forma p/q, donde p y q son números enteros y q ≠ 0.

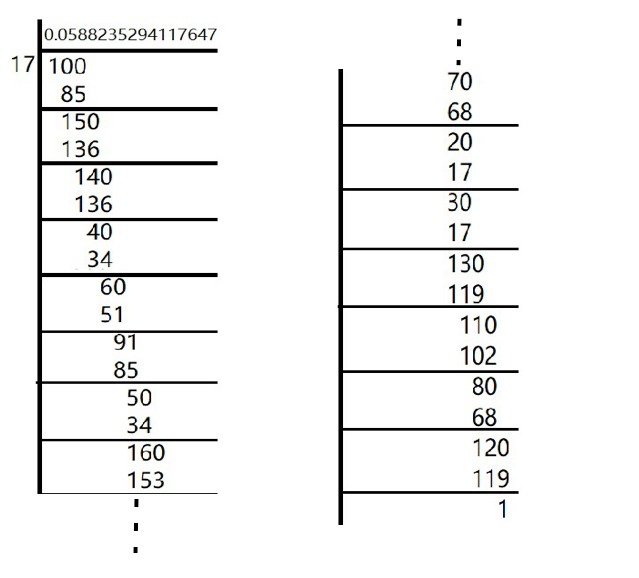
Pregunta 5. ¿Cuál puede ser el número máximo de dígitos en el bloque repetido de dígitos en la expansión decimal de 1/17? Realiza la división para comprobar tu respuesta.

Solución:

En la pregunta dada,

Hay 16 dígitos en el bloque repetido de la expansión decimal de 1/17

Aquí, el resto nunca se convierte en cero y los restos se repiten después de cierta etapa.

Por lo tanto, la expansión decimal es recurrente sin terminación.

1/17 = $0.\overline{0588235294117647}$

Pregunta 6. Mire varios ejemplos de números racionales en la forma p/q (q ≠ 0), donde p y q son números enteros sin factores comunes distintos de 1 y que tienen representaciones decimales terminales (expansiones). ¿Puedes adivinar qué propiedad q debe satisfacer?

Solución:

Observamos que cuando q es 2, 4, 5, 8, 10… Entonces la expansión decimal está terminando.

Pongamos algún ejemplo,

1/2 = 0. 5, denominador q = 2 ¹

7/8 = 0. 875, denominador q =2 ³

4/5 = 0. 8, denominador q = 5 ¹

Por lo tanto, concluimos que se puede obtener un decimal terminal en la situación en la que

la factorización prima del denominador de las fracciones dadas tiene la potencia

de solo 2 o solo 5 o ambos.

En forma de 2 ^m × 5 ⁿ , donde n, m son números naturales.

Pregunta 7. Escribe tres números cuyas expansiones decimales sean no terminales no recurrentes.

Solución:

Como sabemos, todos los números irracionales son no recurrentes y no terminales.

Asi que,

√5 = 2.23606798…….

√27 =5.19615242……

√41 = 6.40312424…..

Pregunta 8. Encuentra tres números irracionales diferentes entre los números racionales 5/7 y 9/11.

Solución:

Como, expansión decimal de

5/7 = $0.\overline{714285}$

9/11 = $0.\overline{81}$

Por lo tanto, tres números irracionales diferentes entre ellos pueden ser los siguientes,

0.73073007300073000073…

0.75075007300075000075…

0.76076007600076000076…

Pregunta 9. Clasifica los siguientes números como racionales o irracionales:

(yo) √23

Solución:

√23 = 4.79583152……

Como el número es no recurrente no terminante.

Es un número irracional .

(ii) √225

Solución:

√225 = 15 = 15/1

Como el número se puede representar en forma p/q, donde q ≠ 0.

Es un número racional .

(iii) 0.3796

Solución:

Como, el número 0.3796, está terminando.

Es un número racional .

(iv) 7.478478…

Solución:

Como, el número 7.478478, no termina pero es recurrente.

Es un número racional .

(v) 1.101001000100001…

Solución:

Como, el número 1.101001000100001…, no termina pero es recurrente.

Es un número racional .

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Escriba lo siguiente en forma decimal y diga qué tipo de expansión decimal tiene cada uno:

(yo) 36/100

(ii) 1/11

(iii)

(iv) 3/13

(v) 2/11

(vi) 329/400

Pregunta 2. Sabes que = ¿Puedes predecir cuáles son las expansiones decimales de sin hacer la división larga? ¿Si es así, cómo?

[Sugerencia: estudie los restos mientras encuentra el valor de 1/7 cuidadosamente.]

Pregunta 3: Exprese lo siguiente en la forma p/q, donde p y q son números enteros y q ≠ 0.

(i)

(ii)

(iii)

Pregunta 4. Expresar 0.99999…. en la forma p/q, ¿Te sorprende tu respuesta? Con tu maestro y compañeros de clase discute por qué la respuesta tiene sentido.

Pregunta 5. ¿Cuál puede ser el número máximo de dígitos en el bloque repetido de dígitos en la expansión decimal de 1/17? Realiza la división para comprobar tu respuesta.

Pregunta 6. Mire varios ejemplos de números racionales en la forma p/q (q ≠ 0), donde p y q son números enteros sin factores comunes distintos de 1 y que tienen representaciones decimales terminales (expansiones). ¿Puedes adivinar qué propiedad q debe satisfacer?

Pregunta 7. Escribe tres números cuyas expansiones decimales sean no terminales no recurrentes.

Pregunta 8. Encuentra tres números irracionales diferentes entre los números racionales 5/7 y 9/11.

Pregunta 9. Clasifica los siguientes números como racionales o irracionales:

(yo) √23

(ii) √225

(iii) 0.3796

(iv) 7.478478…

(v) 1.101001000100001…

Deja una respuesta Cancelar la respuesta

(iii) $4\frac{1}{8}$

Pregunta 2. Sabes que $\frac{1}{7}$ = $0.\overline{142857}$ ¿Puedes predecir cuáles son las expansiones decimales de $\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$ sin hacer la división larga? ¿Si es así, cómo?

(i) $0.\overline{6}$

(ii) $0.4\overline{7}$

(iii) $0.\overline{001}$