Clase 9 Soluciones NCERT – Capítulo 10 Círculos – Ejercicio 10.5

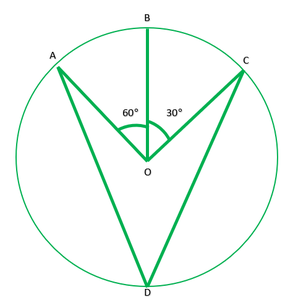
Pregunta 1. En la fig. 10.36, A, B y C son tres puntos en un círculo con Centro O tales que ∠BOC=30° y ∠AOB=60°. Si D es un punto en el círculo que no sea el arco ABC, encuentre ∠ADC.

Solución:

Dado: ∠BOC=30° y ∠AOB=60°
Para encontrar: ∠ADC
Solución: ∠AOC=2∠ADC ———[El ángulo subtendido por un arco en el centro es el doble del ángulo el ángulo subtendido por cualquier punto en la parte restante del círculo.]
∠AOB+∠BOC=2∠ADC
60°+30°=2∠ADC
90+30=2∠ADC
90/2=∠ADC
45=∠ADC

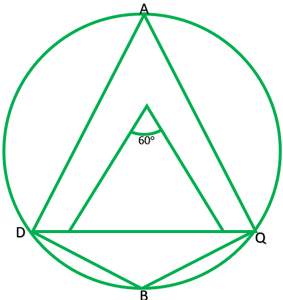
Pregunta 2. Una cuerda de un círculo es igual al radio del círculo. Encuentre el ángulo subtendido por la cuerda en un punto del arco menor y también en un punto del arco mayor.

Solución:

Dado: PQ=OP
Para encontrar: ¿El ángulo en el arco mayor es ∠A=?
El ángulo sobre el arco menor es ∠B=?
Dado que, =PO=OQ 
∴∠POQ=60° 
∠POQ=2∠PAQ [El ángulo subtendido por un arco en el centro es el doble del ángulo subtendido por cualquier punto en el punto restante del círculo]
Reflejo ∠POQ=360 °-60°
Reflejo ∠POQ=300°
Reflejo ∠POQ=2∠POQ
300°=2∠PBQ
300°/2=∠PBQ
150°=∠PBQ

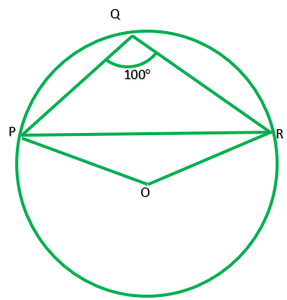
Pregunta 3. En la fig. 10.37, ∠PQR=100°, donde P, Q y R son los puntos en un círculo con centro en O. Halla ∠OPR.

Solución:

Dado: ∠PQR=100°
Para encontrar: ∠OPR=?
Reflejo ∠POR=2∠PQR ——–[ El ángulo subtendido por un arco en el centro es el doble del ángulo subtendido por él en cualquier punto del resto del círculo]
Reflejo ∠PQR=2*100
=200°
∠POR= 360°-200°
Ahora en ∆POR,OP=QR [Radios del mismo círculo]
∠P=∠R y cada uno =x.
∴∠P+∠O+∠R=180° [propiedad de suma de ángulos de ∆]
x+160°+x=180°-160°
2x+160°=180°
x=20°/2=10°
∴∠OPR=10 °

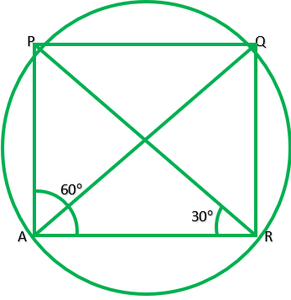
Pregunta 4. En la fig. 10.38, ∠ADC=69°,∠ACB=31°, encuentre ∠BDC.

Solución:

Dado: ∠ABC=69°,∠ACB=31°
Para encontrar: ∠BDC=?
Solución: En ∆ABC
∠A+∠B+∠C=180° ———[Propiedad de la suma de ángulos de ∆]
∠A+69°+31°=180°
∠A=180°-100°
∠A=80°
∠A y ∠D se encuentran en el mismo segmento, por lo tanto,
∠D=∠A
∠D=80°
∠BDC=80°

Pregunta 5. En la fig., A, B, C y D son cuatro puntos en un círculo. AC y BD se intersecan en un punto E tal que ∠BEC=130° y ∠ECD=20°. Encuentre ∠BAC.

Solución:

Dado: ∠BEC=130°,∠ECD=20°
Para encontrar: ∠BAC?
Solución: En ∆EDC
∠E=180°-130° ———[par lineal]
∠E=50°
∠E+∠C+∠D=180° ——[propiedad de la suma de ángulos del triángulo]
50°+20°+∠ D=180°
70°+∠D=180°
∠D=180/70=110°
Ya que, ∠A y ∠D son rectas en el mismo segmento 
∴∠A=∠D 
∠A=110°
∠BAC=110°

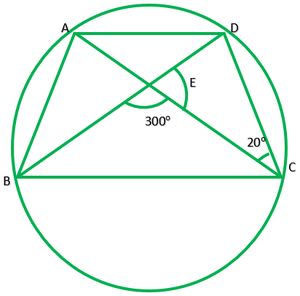
Pregunta 6. ABCD es un cuadrilátero cíclico cuyas diagonales se cortan en un punto E. Si ∠DBC =70°, ∠BAC es 30°, encuentra ∠BCD. Además, si AB=BC, encuentra ∠ECD.

Solución:

Dado: ABCD es una intersección diagonal de cuadrilátero cíclico en E ∠DBC=70°, ∠BAC es 30°. Si AB=BC.
Para encontrar: ∠BCD y ∠ECD
∠BDC=∠BAC=30° ——-[ángulo en el mismo segmento]
En ∆BCD,
∠B+∠C+∠D=180° ——–[propiedad de la suma de ángulos del triángulo]
∠ C+100°=180°
∠C=180°-100°=80°
∴∠BCD=80°
Si AB=BC,
Entonces, ∠BAC=∠BCA
30°=∠BCA
Ahora, ∠BCA+∠ECD=∠BCD
30°+∠ECD=80°
∠ECD=80°-30°
∴∠ECD=50°

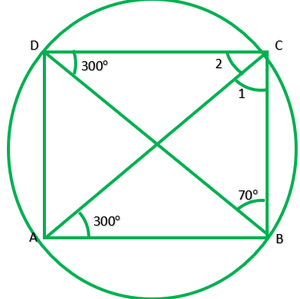
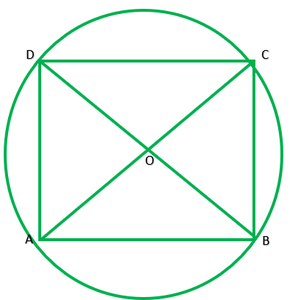
Pregunta 7. Si las diagonales de un cuadrilátero cíclico son diámetros del círculo a través de los vértices del cuadrilátero, prueba que es un rectángulo.

Solución:

Dado: ABCD es un cuadrilátero cíclico. Las diagonales de ABCD también son diámetros de un círculo.
Para probar: ABCD es un rectángulo
AC=BD ———-[diámetros del mismo círculo]
OA=OA ———[radios del mismo círculo]
OA=OC=1/2AC ———2
OB=OD=1/ 2BD ———-2
De I y 2 diagonales son iguales y se bisecan
∴ABCD es un rectángulo

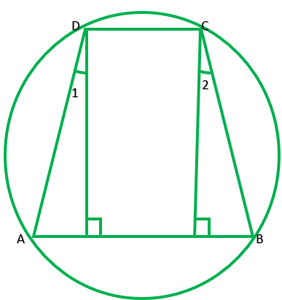
Pregunta 8. Si los lados no paralelos de un trapecio son iguales, prueba que es cíclico.

Solución:

Dibujar DL perpendicular AB y EF perpendicular AB
In ∆DEA y ∆CEB
∠E=∠F ——–[cada 90°]
AD=BC ——–[dado]
DE=CF ——–[distancia entre || las líneas son iguales en todas las líneas]
∴∆DEA≅∆CFB ——–[RHS]
∠A=∠B ———[by cpct] 1
∠1=∠2 (de 1)
Sumando 90° en cada lado
∠1+90 °=∠2+90°
∠1+∠EDC=∠2+FCD
∠ADC=∠BCD
∠D=∠C 2
Ahora,
∠A+∠A+∠C+∠C=360°
2∠A+2∠C=360 °
2(∠A+∠C)=360°
∠A+∠C=360°/2=190°
Porque la suma de los ángulos opuestos es 180°.
ABCD es paralelogramo.

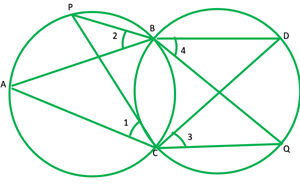
Pregunta 9. Dos círculos se intersecan en dos puntos B y C. A través de B, se dibujan dos segmentos de línea ABD y PBQ para intersecar los círculos en A, D y P, Q respectivamente (ver fig. 10.40). Demuestra que ∠ACP=∠QCD.

Solución:

Para probar: ∠ACP=∠QCD o ∠1=∠2
∠1=∠2 —— [los ángulos en el mismo segmento son iguales] 1
∠ 3=∠ 4 ——- [los ángulos en el mismo segmento son iguales] 2
∠ 2=∠4 ——- [ángulos opuestos verticalmente] 3
De 1 2 y 3
∠1=∠3
∴∠ACP=∠QCB

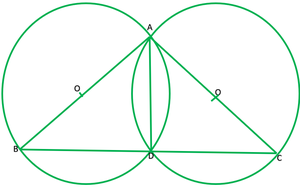
Pregunta 10. Si se dibujan círculos tomando como diámetros dos lados de un triángulo, demuestre que el punto de intersección de estos círculos se encuentra en el tercer lado.

Solución:

Dado: ABC es ∆ y AB y AC son diámetros de dos círculos
Para demostrar: El punto de intersección es D, se encuentra en BC.
Construcción: Unir AD
∠ADB=90° ——-[ángulos en semicírculo] 1
∠ADC=90 ° ——[ángulos en semicírculo] 2
Sumar 1 y 2
∠ADB+∠ADC=90°+90°
∠BDC=180°
BDC es una línea recta, por lo tanto, D se encuentra en BC.

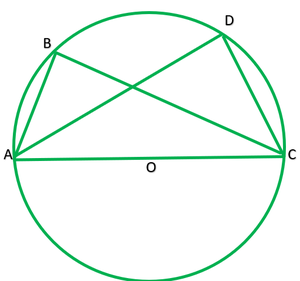
Pregunta  11. ABC y ADC son dos triángulos rectángulos con hipotenusa común AC. Demuestra que ∠CAD=∠CBD.

Solución:

Dado: ABC y ADC son dos triángulos rectángulos con hipotenusa común AC.
Para probar: ∠ADB=∠CBD
Solución: ∠ABC=∠ADC=90°
Círculo dibujado tomando AC como diámetro que pasa por B y D.
Para cuerda CD 
∠CAD=∠CBD ——-[ángulo en el mismo segmento]

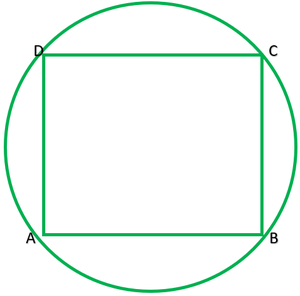
Pregunta 12. Demuestra que un paralelogramo cíclico es un rectángulo.

Solución:

Dado: ABC es un cíclico ||gm 
Para probar: ABCD es un rectángulo.
Porque ABCD es un cíclico ||gm
∴∠A+∠C=180°
∠A=∠C [ángulo opuesto de ||gm]
∴∠A=∠C=(180°)/2=90° 
∠A=90°
∠C=90°
Del mismo modo,
∠B+∠D=180°
∴∠B=∠D =(180°)/2=90° ———-[opuesto a ||gm]
Cada ángulo de ABCD es 90° 
∠ B=90°
∠D=90°
Entonces, ABCD es un rectángulo.