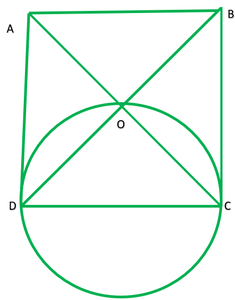
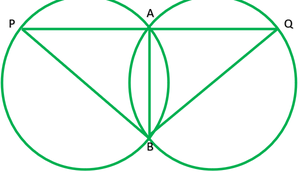
Pregunta 1. Demostrar que la línea de centros de dos círculos que se cortan subtiende ángulos iguales en los dos puntos de intersección.
Solución:
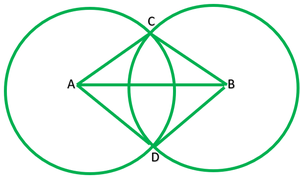
Dado: Dos círculos con Centro A y B se cruzan en C y D.
Para probar: ∠ACB=∠ADB
Construcción: Une AD,BC y BD
Prueba: En ∆ACB y ∆ADB
AC=AD ——–[radios del mismo círculo]
BC=BD ———[radios del mismo círculo]
AB=AB ——–[común]
∴∆ACB≅∆ADB ——— [por SSS]
∠ACB=∠ADB ——–[cpct]
Pregunta 2. Dos cuerdas AB y CD de longitudes de 5 cm y 11 cm respectivamente de un círculo son paralelas entre sí y están en lados opuestos de su centro. Si la distancia entre AB y CD es de 6 cm, encuentra el radio del círculo.
Solución:
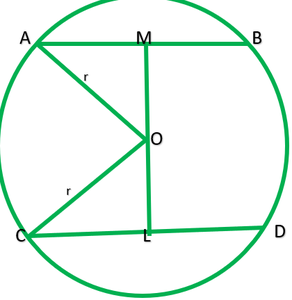
Sea O el centro de la circunferencia y sea r cm
Dado: AB=5cm, CD=11cm
Construcción: Dibuje OM perpendicular AB y OL perpendicular CD.
Porque OM perpendicular AB y OL perpendicular CD y AB||CD.
∴Los puntos O, L y M son colineales, entonces ∠M=6cm
Sea OL=x
Entonces OM=6=x
Únete a AO y CO
OA=OC =r
OL=1/2CD=1/2*11=5,5 cm —–[perpendicular desde la bisectriz de la cuerda]
AM=1/2AB=1/2*5=2.3cm —–[perpendicular desde la bisectriz de la cuerda]
Ahora, en ∆DLC derecho
r 2 =(OL) 2 +(CL) 2
r 2 = x 2 + (5.5) 2
r 2 =x 2 +30.25 ———–1
Ahora en ∆OMA derecho
r 2 =(OM) 2 +(MA) 2
r 2 = (6-x) 2 + (2.5) 2
r2 = 36+x2 = 12x+6,25
r 2 =x 2 -12x+42.25 ———–2
Ahora igualando la ecuación 1 y 2
X2 + 30,25=x2 -12x + 30,25
12x=42,25-30,25
X=12/12=1
Poner el valor de x en la ecuación 1
r 2 =x 2 +30.25
r2 =(1 ) 2 +30,25
r2 = 31,25
r=√31,25=5,6 (aprox.)
El radio del círculo es de 5,6 cm.
Pregunta 3. Las longitudes de dos cuerdas paralelas de un círculo son 6 cm y 8 cm. Si la cuerda más pequeña está a una distancia de 4 cm del centro, ¿cuál es la distancia de la otra cuerda al centro?
Solución:
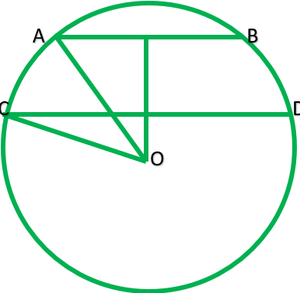
Sean AB y CD|| cuerda de circunferencia de centro O que AB=6cm y CD=8cm y radio de circunferencia =r cm.
Construcción: Dibuje OP perpendicular AB y OM perpendicular CD.
Porque AB||CD y OP perpendicular AB y OM perpendicular CD por lo tanto. Los puntos O, M y P son colineales.
Claramente, OP=4cm ———-[Según pregunta]
OM=encontrar?
P es el punto medio de AB.
∴AP=1/2 AB=1/2*6=3cm
M es el punto medio de AB.
CM = 1/2 CD = 1/2*8 cm = 4 cm
Únete a AO y CO
Ahora en ∆OPA derecha,
r 2 = AP 2 + PO 2
r 2 = 3 2 + 4 2
r 2 = 9 + 16 = 25
Ahora en ∆OMC
r2 = CM2 + MO2 _
25=4 2 +MO 2
25-16 = MES 2
9=MO 2
√9=MES
3=MES
∴Por lo tanto, la distancia de la otra cuerda desde el centro es de 3 cm.
Cuestión 4. Sea el vértice de un ángulo ABC fuera de un círculo y los lados del ángulo corten cuerdas iguales AD y CE con el círculo. Demuestra que ∠ABC es igual a la mitad de la diferencia de los ángulos subtendidos por las cuerdas AC y DE en el centro.
Solución:
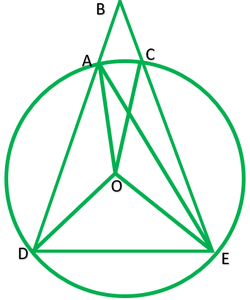
Dar: El vértice B de ∆ABC está fuera del círculo, cuerda AD=CE
Para probar: ∠ABC=1/2(∠DOE-∠AOC)
Construcción: Únete a AE
Solución: La cuerda DE subtiende ∠DOE en el centro y ∠DAE en el punto A del círculo.
∴∠DAE=1/2∠DOE ———-1
cuerdas AC subtiende ∠AOC en el centro y ∠AEC en el punto
∴∠AEC=1/2∠AOC ———2
En ∆ ABE,∠DAE es el ángulo exterior
∠DAE=∠ABC+∠AEC
1/2∠DOE=∠ABC+1/2∠AOC
½(∠DOE-∠AOC)= ∠ABC
Pregunta 5. Demostrar que el círculo trazado con cualquier lado de un rombo como diámetro, pasa por el punto de intersección de sus diagonales.
Solución:
Dado: Un rombo ABCD en el que O es el punto de intersección de las diagonales AC y BD.
Se dibuja un círculo tomando CD como diámetro.
Para probar: los puntos del círculo a través de O o Mentiras en los círculos.
Prueba: En rombo ABCD,
∠DOA=90° ——–[las diagonales del rombo se cortan a 90°] 1
En círculo:
∠COD=90° ——–[el ángulo formado en el segmento O es un ángulo recto] 2
De 1 y 2
O miente en el círculo.
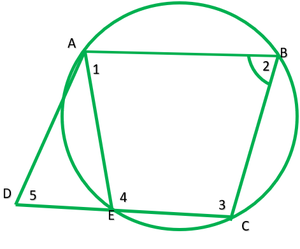
Pregunta 6. ABCD es un paralelogramo. El círculo a través de A, B y C interseca a CD (producido si es necesario) en E. Demuestre que AE = AD.
Solución:
ABCD es un ||gm. El círculo que pasa por A, B y C se corta en E.
Para probar: AE=AD
Prueba: Aquí ABCE es un cuadrilátero cíclico
∠2+∠4=180° —–[la suma de los opuestos es de un cuadrilátero cíclico es 180°]
∠4=180°-∠1 ——-1
Ahora ∠4+∠6=180°-∠6 ———2
De 1 y 2
180°-∠2=∠180°-∠6
∠2=∠6 ———–3
También ∠2=∠5 ———[los ángulos opuestos de ||gm son iguales] —–4
De 3 y 4
∠5=∠6
Ahora, en ∆ADE,
∠5=∠6
∴AE=AD ——[los lados opuestos a ángulos iguales en a∆ son iguales]
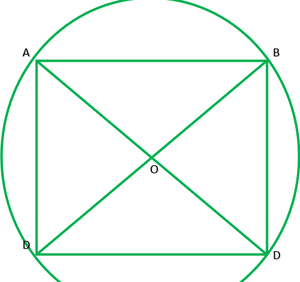
Pregunta 7. AC y BD son cuerdas de un círculo que se bisecan entre sí. Demuestre que (i) AC y BD son diámetros, (ii) ABCD es un rectángulo.
Solución:
Dado: dos cuerdas AC y BD se bisecan, es decir, OA = OC, OB = OD
Demostrar: En ∆AOB y COB
AO=CO ——-[dado]
∠AOB=∠COD ——[ángulo verticalmente opuesto]
OB=OD ——–[dar]
∴∆AOB≅∆COB ——[sss]
AB=CD ——[CPCT] 1
de manera similar ∆AOD≅∆COB (SAS)
DA=CD (CPCT) 2
De 1 y 2 ABCD es un ||gm
Como ABCD es un cuadrilátero cíclico
∴∠A+∠C=180°
∠B+∠B=180°
2∠B=180°
∠B=180°/2
∠B=90°
∴ ∠A y ∠B se encuentran en un semicírculo
→ AC y BD son el diámetro del círculo.
ii) Como ABCD es un ||gm y ∠A=90°
∴ ABCD es un rectángulo.
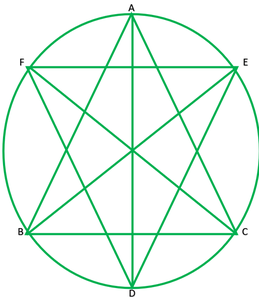
Pregunta 8. Las bisectrices de los ángulos A, B y C de un triángulo ABC intersecan su circunferencia circunscrita en D, E y F respectivamente. Demuestra que los ángulos del triángulo DEF son 90° – 1 2 A, 90° – 1 2 B y 90° – 1 2 C.
Solución:
Dado:∆ABC y su circunferencia AD,BE y CF son bisectrices de ∠A,∠B y ∠C
Respectivamente.
A prueba:∠ D=90°-1/2∠A , ∠E=90°-1/2∠B , ∠F=90°-1/2∠C
Construcción: Unir AE y AF.
Solución: ∠ADE=∠ABE ———-1 [los ángulos en el mismo segmento son iguales]
∠ADF=∠ACF ———–2 [los ángulos en el mismo segmento son iguales]
sumando 1 y 2
∠ADE+∠ABF=∠ABE+∠ACF
∠D=1/2∠B+1/2∠C ——[BC y CF son bisectrices de ∠B y ∠c]
∠D=1/2(∠B+∠C)
∠D=1/2(180°-∠A)
∠D=1/2(180°-∠A)
∠D=90°-1/2∠AC
Pregunta 9. Dos círculos congruentes se intersecan en los puntos A y B. A través de A se dibuja cualquier segmento de línea PAQ de modo que P, Q se encuentren en los dos círculos. Demuestre que BP = BQ.
Solución:
Dado: dos círculos congruentes que se cortan en A y B.
PAB es un segmento de recta
Para probar: BA=BQ
Construcción: únete a AB
Prueba: AB es un acorde común de ambos círculos congruentes.
El segmento de ambos círculos será igual.
∠P=∠Q
Ahora, en ∆ BPQ,
∠P=∠Q
BP=BQ ——[los lados opuestos a los ángulos iguales son iguales]
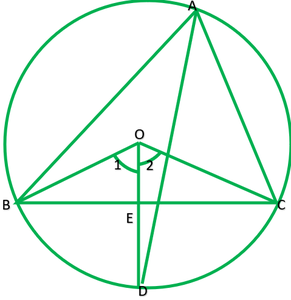
Pregunta 10. En cualquier triángulo ABC, si la bisectriz del ángulo de ∠A y la bisectriz perpendicular de BC se intersecan, prueba que se intersecan en el circuncírculo del triángulo ABC.
Solución:
Dado: A ∆ABC, en el que AD es la bisectriz de ∠A y OD es ⊥ bisectriz de BC.
Para probar: D se encuentra en el circuncírculo.
Construcción: unir OB y OC
Prueba: Dado que BC subtiende ∠BAC en A en el resto del círculo.
∠BOC=2∠BAC ——-1
Ahora, en ∆BOE y ∆ COE
BO=OE ——–(radios de la misma circunferencia)
BE=CE —–(dar)
∴∆BOE≅COE ——-(SSS)
∠1=∠2 ——-(cpct)
Ahora,
∠1+∠2=∠BOC
2∠1=∠BOC
2∠1=2∠BAC ———- (desde 1)
∠1=∠BAC
∠BOE=∠BAF
∠DBO=∠BAC
∠BOD=2∠BAD [AD es la bisectriz de ∠BAC]
Esto es posible solo si BD es la cuerda del círculo.
D se encuentra en el círculo.
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA