Pregunta 1. Dibujar la gráfica de cada una de las siguientes ecuaciones lineales en dos variables:
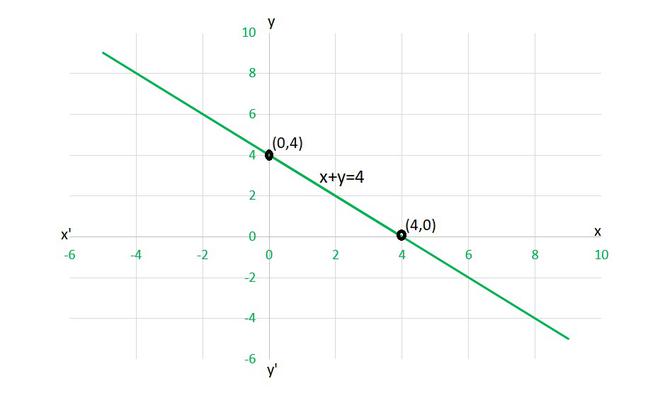
(yo) x + y = 4
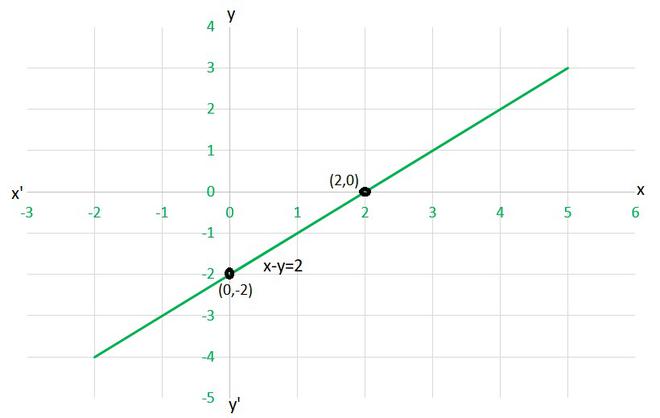
(ii) x – y = 2
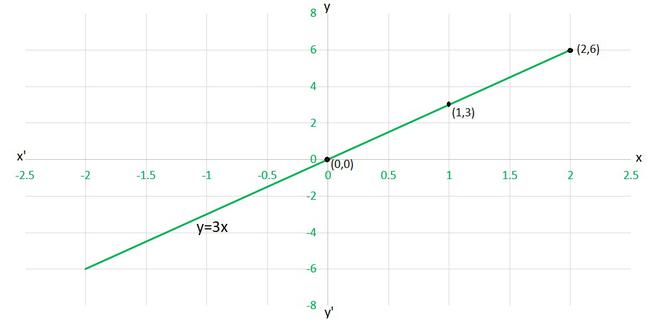
(iii) y = 3x
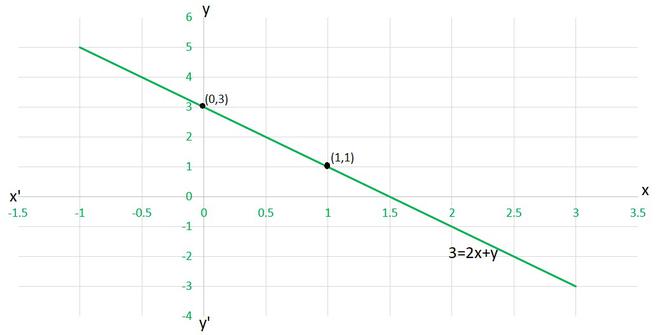
(iv) 3 = 2x + y
Solución:
(i) Para dibujar el gráfico x+y=4 , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y = 4,
y x = 4, y = 0
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 4 4 0
(ii) Para dibujar el gráfico xy=2 , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y = -2,
y x = 2, y = 0
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 -2 2 0
(iii) Para dibujar el gráfico y=3x , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y = 0,
y x = 1, y = 3
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 0 1 3
(iv) Para dibujar el gráfico 3=2x+y , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y =3,
y x = 1, y = 1
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 3 1 1
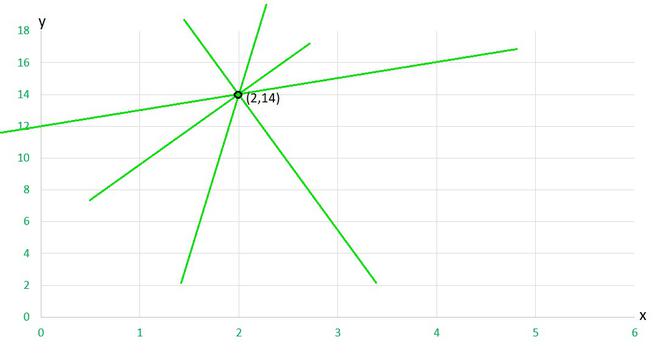
Pregunta 2. Da las ecuaciones de dos rectas que pasan por (2, 14). ¿Cuántas líneas más hay y por qué?
Solución:
Aquí, dado que el punto es (2,14), entonces
x=2 y y=14
Podemos formar varias ecuaciones tales como,
yx = 14-2 = 12
x+y = 2+14 =16
2x+y = 4+14 = 18
y-2x = 14-4 = 10
y = 14
x = 2
y muchos más……..
De hecho, existen infinitas ecuaciones lineales que se satisfacen con las coordenadas del punto (2, 14).
Como se dice que puede haber infinitas líneas que pasan por un punto. Así que aquí,
⟹
Pregunta 3. Si el punto (3, 4) está en la gráfica de la ecuación 3y = ax + 7, encuentra el valor de a.
Solución:
La ecuación dada es
3y = hacha+7
Según el punto dado (3,4),
x = 3 y y = 4
Como este punto se encuentra en este gráfico, entonces satisfará estos puntos. Entonces reemplazando los valores
3y = hacha+7
⟹ (3×4) = (a×3)+7
12 = 3a+7
3a = 12–7
3a = 5
un =
Por lo tanto, el valor de a =
.
Pregunta 4. La tarifa de taxi en una ciudad es la siguiente: Para el primer kilómetro, la tarifa es de 8 ₹ y para la distancia posterior es de 5 ₹ por kilómetro. Tomando la distancia recorrida como x km y la tarifa total como ₹ y, escribe una ecuación lineal para esta información y dibuja su gráfico.
Solución:
Entonces, como se indica en la pregunta, tomaremos
Distancia recorrida en x km
y la tarifa total en $y
Tarifa del primer kilómetro = 8 por km
Tarifa después del primer 1 km = ₹ 5 por km
Sea x la distancia total, entonces la distancia después de un kilómetro será = (x-1)km
Por lo tanto, Tarifa después del primer km = 5(x-1)
Entonces, en forma de ecuación podemos concluir que,
La tarifa total = Tarifa del primer kilómetro + tarifa después del primer kilómetro
y = 8+5(x-1)
y = 8+5(x-1)
y = 8+5x – 5
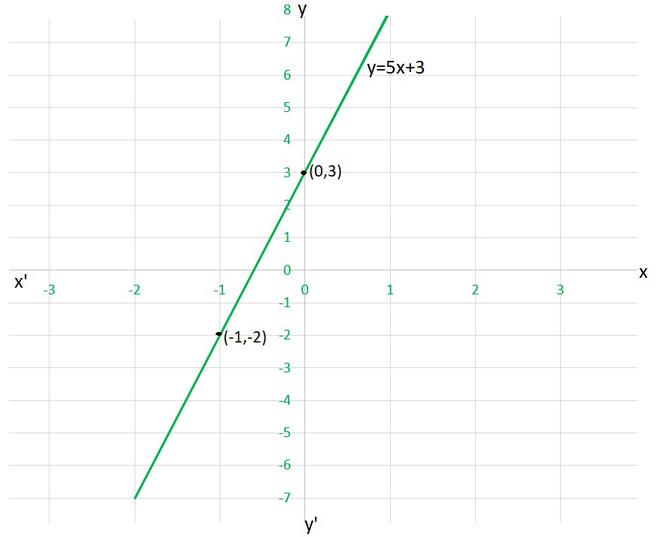
y = 5x+3
Para dibujar el gráfico y=5x+3 , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y =3,
y x = -1, y = -2
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 3 -1 -2
Pregunta 5. De las opciones dadas a continuación, elija la ecuación cuyas gráficas se dan en la Fig. 4.6 y la Fig. 4.7.
Para la Fig. 4. 6
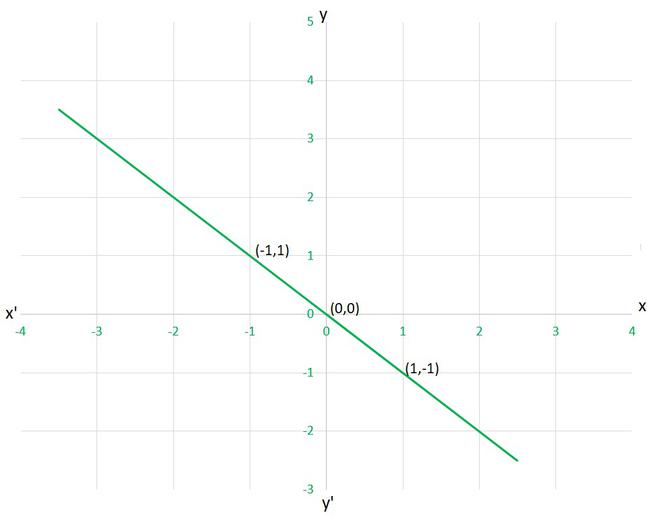
(yo) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x
Solución:
Verifiquemos cada caso dado, ya sea que satisfagan la solución dada en el gráfico o no,
(yo) y=x
como punto dado (1,-1)
x=1 y y=-1 ⟹ x≠y
Por lo tanto, esta ecuación es INCORRECTA para este gráfico.
(ii) x+y=0
como punto dado (1,-1), (1,-1) y (0,0)
x=1 y y=-1 ⟹ x+y=0
x=-1 y y=1 ⟹ x+y=0
x=0 y y=0 ⟹ x+y=0
Por lo tanto, esta ecuación es CORRECTA para este gráfico.
(iii) y=2x
como punto dado (1,-1)
x=1 y y=-1 ⟹ y≠2x
Por lo tanto, esta ecuación es INCORRECTA para este gráfico.
(iii) 2+3y=7x
como punto dado (1,-1)
x=1 y y=-1 ⟹ 2+3y≠7x
Por lo tanto, esta ecuación es INCORRECTA para este gráfico.
Para la figura 4.7
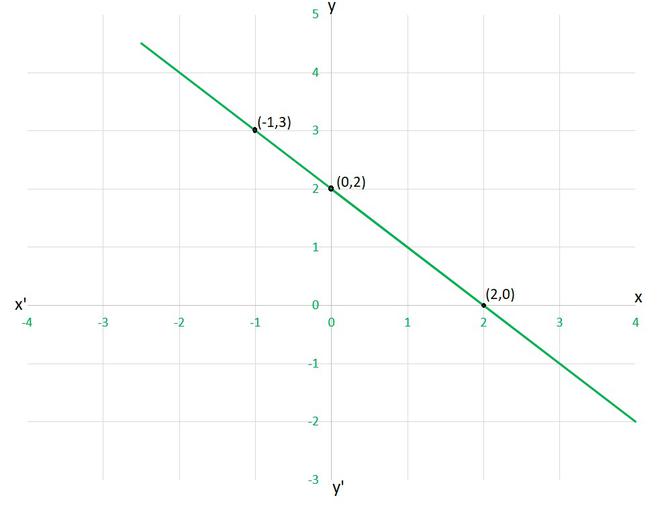
(yo) y = x + 2
(ii) y = x – 2
(iii) y = –x + 2
(iv) x + 2y = 6
Solución:
Verifiquemos cada caso dado, ya sea que satisfagan la solución dada en el gráfico o no,
(yo) y=x+2
dado el punto (0,2), (2,0) y (-1,3)
x=0 y y=2 ⟹ y=x+2
x=2 y y=0 ⟹ y≠x+2
Por lo tanto, esta ecuación es INCORRECTA para este gráfico.
(ii) y=x-2
como punto dado (0,2)
x=0 y y=2 ⟹ y≠x-2
Por lo tanto, esta ecuación es INCORRECTA para este gráfico.
(iii) y=-x+2
como punto dado (0,2)
x=0 y y=2 ⟹ y=-x+2
x=2 y y=0 ⟹ y=-x+2
x=-1 y y=3 ⟹ y=-x+2
Por lo tanto, esta ecuación es CORRECTA para este gráfico.
(iii)x+2y=6
como punto dado (0,2)
x=0 y y=2 ⟹ x+2y≠6
Por lo tanto, esta ecuación es INCORRECTA para este gráfico.
Pregunta 6. Si el trabajo realizado por un cuerpo al aplicarle una fuerza constante es directamente proporcional a la distancia recorrida por el cuerpo, exprésalo en forma de ecuación en dos variables y dibuja la gráfica del mismo tomando la fuerza constante como 5 unidades. Lea también en la gráfica el trabajo realizado cuando la distancia recorrida por el cuerpo es
(yo) 2 unidades
(ii) 0 unidad
Solución:
Dado en cuestión,
Trabajo realizado = fuerza × desplazamiento
donde fuerza constante = 5 unidades
tomemos el trabajo hecho como y unidades
y, distancia recorrida por el cuerpo x unidades
Por lo tanto, la ecuación se puede expresar como,
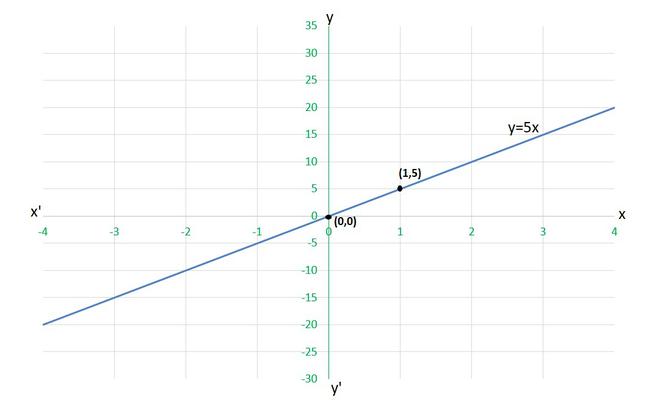
y=5x
Para dibujar el gráfico y=5x , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y = 0,
y x = 1, y = 5
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 0 1 5
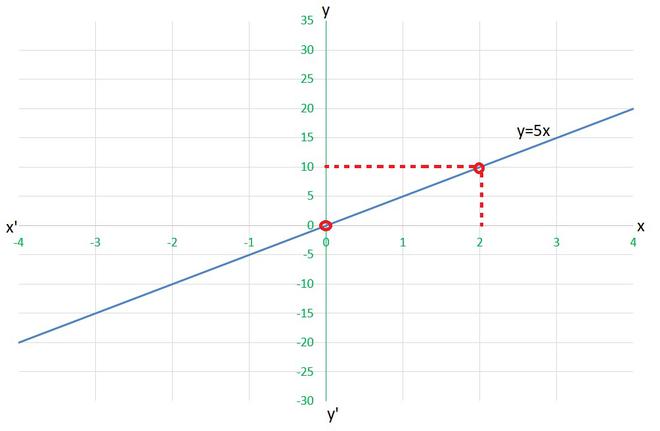
(i) para x= 2 unidades
y=5×2
trabajo realizado = 10 unidades
(ii) para x= 0 unidades
y=5×0
trabajo realizado = 0 unidades
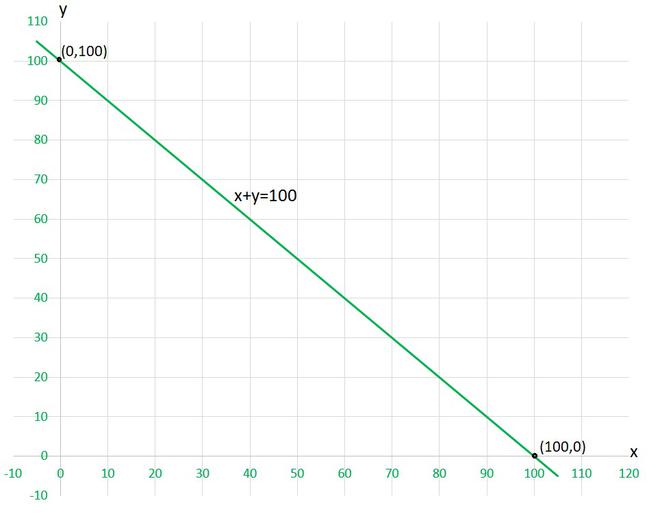
Pregunta 7. Yamini y Fátima, dos estudiantes de la Clase IX de una escuela, contribuyeron juntas con ₹ 100 para el Fondo de Ayuda del Primer Ministro para ayudar a las víctimas del terremoto. Escribe una ecuación lineal que satisfaga estos datos. (Puede tomar sus contribuciones como ₹ x y ₹ y). Dibuja la gráfica de la misma.
Solución:
Tomemos la contribución de Yamini como ₹ x y la contribución de Fátima como ₹ y.
Como juntos contribuyeron ₹ 100, entonces la ecuación se puede formar como,
x+y=100
Para dibujar el gráfico x+y=100 , necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y = 100,
y x = 100, y = 0
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 100 100 0
Pregunta 8. En países como EE. UU. y Canadá, la temperatura se mide en Fahrenheit, mientras que en países como India, se mide en Celsius. Aquí hay una ecuación lineal que convierte Fahrenheit a Celsius:
F = ![]() C+ 32
C+ 32
(i) Dibuje el gráfico de la ecuación lineal anterior usando Celsius para el eje x y Fahrenheit para el eje y.
(ii) Si la temperatura es de 30°C, ¿cuál es la temperatura en Fahrenheit?
(iii) Si la temperatura es de 95 °F, ¿cuál es la temperatura en Celsius?
(iv) Si la temperatura es 0°C, ¿cuál es la temperatura en Fahrenheit y si la temperatura es 0°F, cuál es la temperatura en Celsius?
(v) ¿Existe una temperatura que sea numéricamente la misma tanto en Fahrenheit como en Celsius? Si es así, encuéntralo.
Solución:
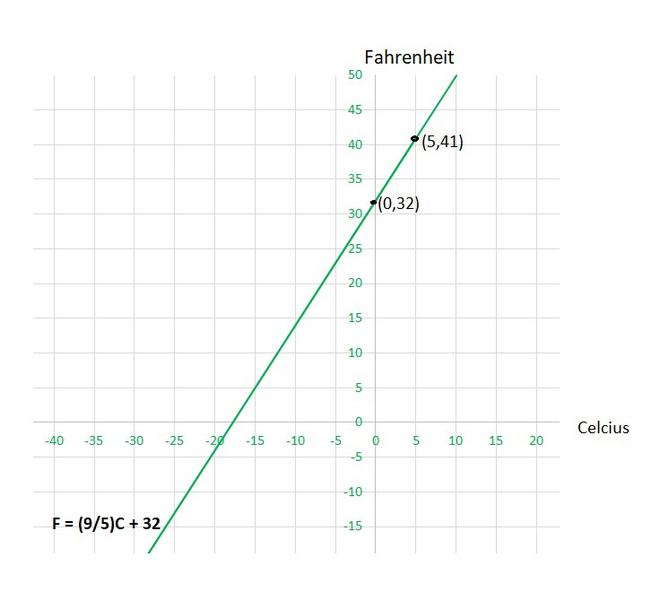
(i) Tomando Celsius en el eje x y Fahrenheit en el eje y, por lo que la ecuación será la siguiente:
y =
x + 32
Para dibujar la gráfica y =
x + 32, necesitamos al menos dos soluciones de la ecuación.
Podemos comprobar que cuando, x = 0, y =32,
y x = 5, y = 41
son soluciones de la ecuación dada. Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 32 5 41
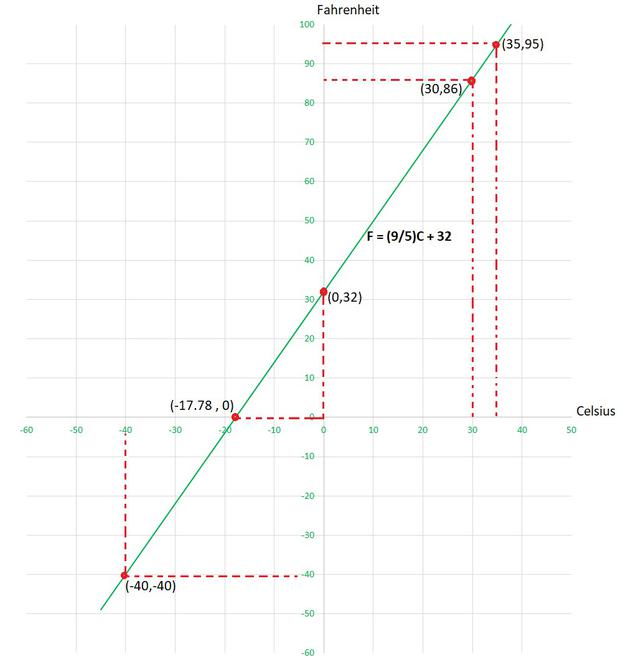
(ii) Cuando la temperatura es de 30°C entonces, usando la ecuación
y =
x + 32
al sustituir, x=30, obtenemos
y =
×30 + 32
y = 86
Por lo tanto, en Fahrenheit la temperatura será de 86°F
(iii) Cuando la temperatura es de 95°F entonces, usando la ecuación
y =
x + 32
al sustituir, y=95, obtenemos
95 =
x+ 32
x =
x = 35
Por lo tanto, en Celsius la temperatura será de 35°C
(iv) Cuando la temperatura es 0°C, usando la ecuación
y =
x + 32
sustituyendo, x=0, obtenemos
y =
×0 + 32
y = 32
Por lo tanto, en Fahrenheit la temperatura será de 32°F
y, cuando la temperatura es 0°F, usando la ecuación y sustituyendo, y=0, obtenemos
0 =
x + 32
x =
x = -17,78
Por lo tanto, en Celsius la temperatura será de -17,78°C.
(v) Tomemos ambas temperaturas igual que x.
entonces, la ecuación queda de la siguiente manera:
x =
x + 32
xx = -32
x = -32
x = -32×
x = -40
Por lo tanto, la temperatura Celsius y Fahrenheit será de -40°C y -40°F respectivamente.
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA