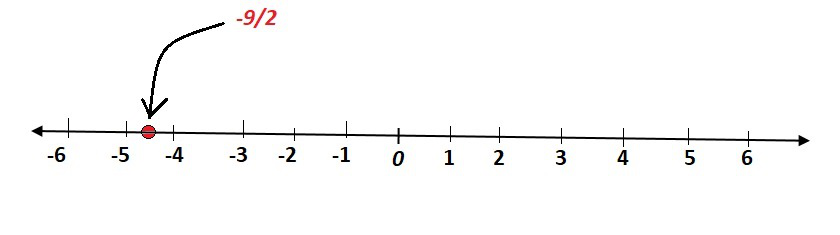Clase 9 Soluciones NCERT- Capítulo 4 Ecuaciones lineales en dos variables – Ejercicio 4.4

Pregunta 1. Dar las representaciones geométricas de y = 3 como una ecuación

(i) en una variable

(ii) en dos variables

Solución:

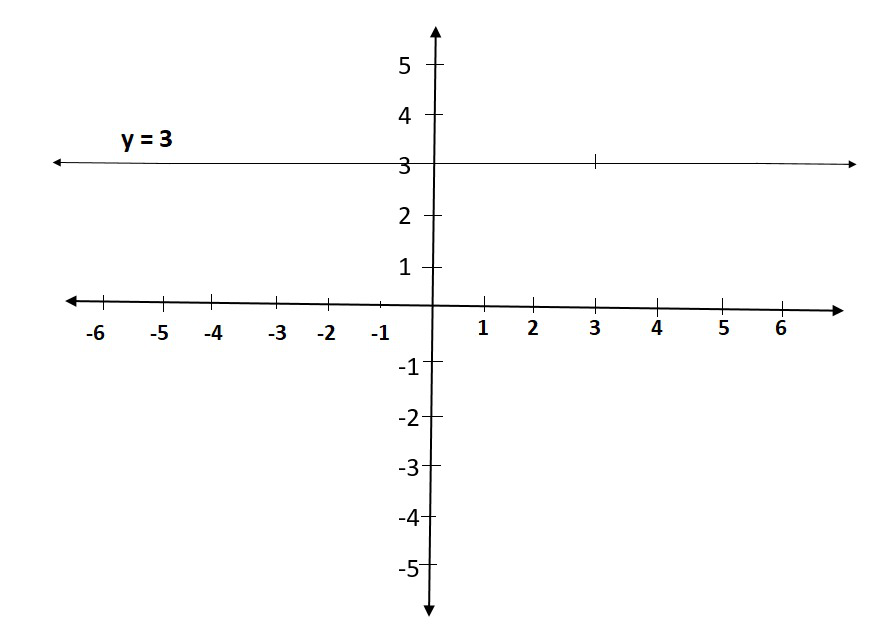
(i) Si y = 3 se trata como una ecuación en una sola variable y, entonces tiene la solución única

y = 3, que es un punto en la recta numérica

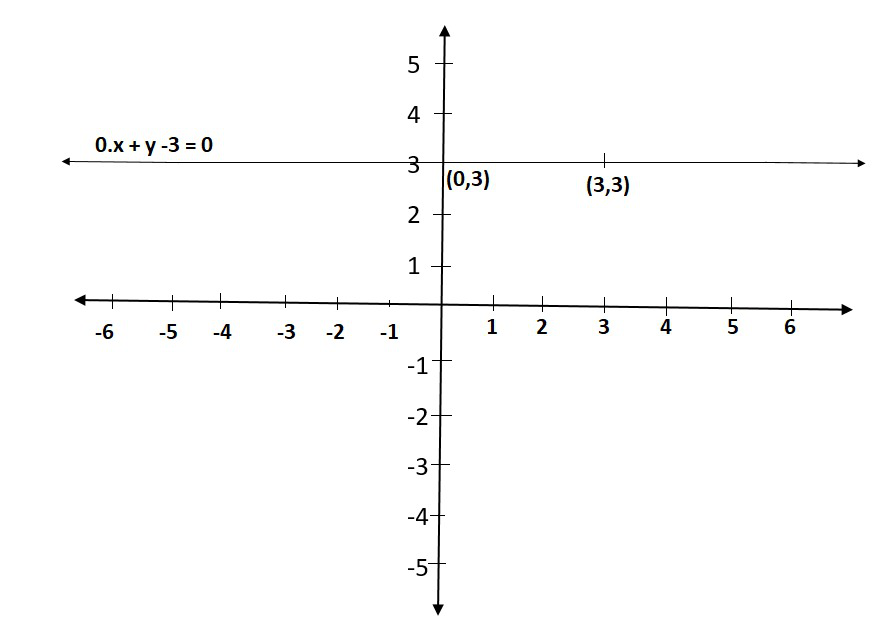
(ii) Cuando una ecuación en dos variables, se puede expresar como,

0.x + y – 3 = 0

que es una ecuación lineal en las variables x e y. Esto se representa con una línea. Ahora todos los valores de x son permisibles porque 0.x siempre es 0. Sin embargo, y debe satisfacer la ecuación y = 3

Esto tiene infinitas soluciones . De hecho, todos son de la forma (r, 3), donde r es cualquier número real, por lo que

Podemos tener estas dos soluciones para hacer una línea en un gráfico como:

X	y
0	3
3	3

Pregunta 2. Dar las representaciones geométricas de 2x + 9 = 0 como una ecuación

(i) en una variable

(ii) en dos variables

Solución:

Primero, resolvemos 2x + 9 = 0, para obtener

x = -9/2

(i) Si x = -9/2 se trata como una ecuación en una sola variable x, entonces tiene la solución única

x = -9/2, que es un punto en la recta numérica.

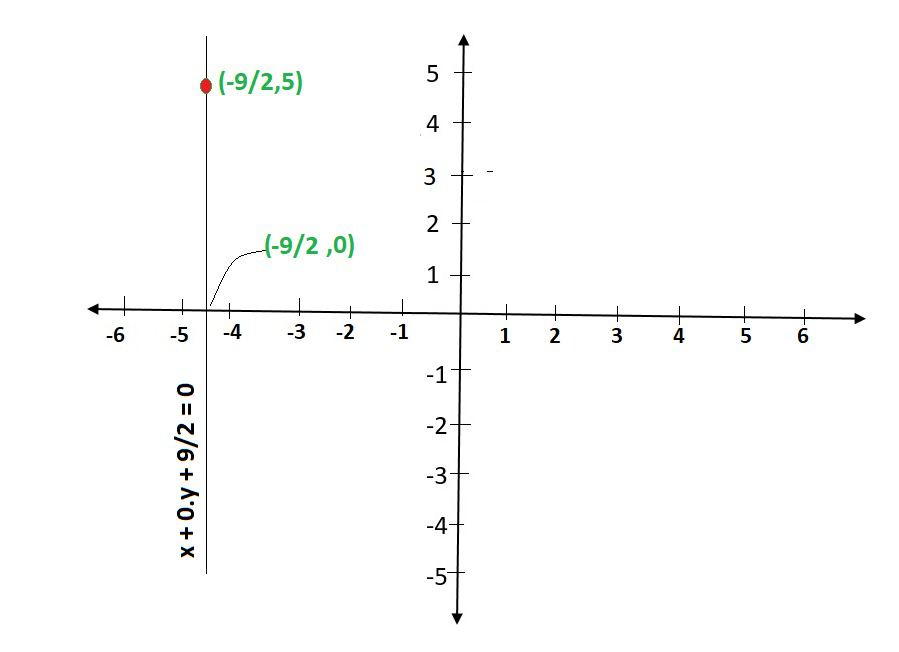
(ii) Cuando una ecuación en dos variables, se puede expresar como,

x + 0.y + 9/2 = 0

que es una ecuación lineal en las variables x e y. Esto se representa con una línea. Ahora todos los valores de y son permisibles porque 0.y siempre es 0. Sin embargo, x debe satisfacer la ecuación x = -9/2

Esto tiene infinitas soluciones . De hecho, todos son de la forma (-9/2, r), donde r es cualquier número real, por lo que

Podemos tener estas dos soluciones para hacer una línea en un gráfico como:

X	y
-9/2	0
-9/2	5