Pregunta 1. ΔABC y ΔDBC son dos triángulos isósceles en la misma base BC y los vértices A y D están en el mismo lado de BC (ver Figura). Si AD se extiende para intersecar a BC en P, demuestre que
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP biseca tanto a ∠A como a ∠D.
(iv) AP es la bisectriz perpendicular de BC.
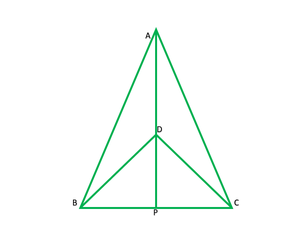
Solución:
Dado: ∆ABC y ∆DCB son isósceles ∆sobre la misma base BC.
Mostrar:
- ΔABD ≅ ΔACD
- ΔABP ≅ ΔACP
- AP biseca tanto a ∠A como a ∠D.
- AP es la mediatriz de BC.
i) en ∆ABD y ∆ACB
AB=CA
BD=CD
ANUNCIO = ANUNCIO
∆ABD≅∆ACD ————-(SSS)
ii) en ∆ABP y ∆ACP
AB=CA
∠ BAP≅∠CAP [∆ABD≅∆ACD POR CPCT]
AP=AP ———[común]
∴[∆ABD≅∆ACD ———–[SAS]
iii) [∆ABD≅∆ACD ———–[SAS]
∠MALO=∠CAD
AD, biseca ∠A
AP, biseca ∠A —————–1
En ∆ BDP y ∆DPB
BD=CD —————(DADO)
DP=PC ———-[∆AB≅ ∆ACP CPCT]
DP=DP ———–[común]
∴∆BDP≅∆CDP (SSS)
∠BDP=∠CDP (CPCT)
DP biseca ∠D
AP biseca ∠D ——————-2
De 1 y 2, AP biseca tanto a ∠ A como a ∠ D
iv) ∠ AP +∠APC =180° ————[par lineal]
∠APB=∠APC ————-[∆ABP≅∆ACP CPCT]
∠APB + ∠APC=180°
2 ∠ APB=180°
∠APB=180/2=90°
BP=PC (DE ii)
∴AP es ⊥ biseca de BC.
Pregunta 2. AD es una altura de un triángulo isósceles ABC en el que AB = AC. Muestra esa
(i) AD biseca a BC (ii) AD biseca a ∠A.
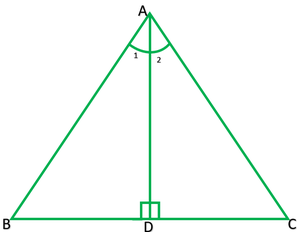
Solución:
Dado: AB=AC, altitud AD
Mostrar:
(i) AD biseca a BC (ii) AD biseca a ∠A.
En ∆ADB y ∆ADC
∠ADB=∠ADC ——– ———–[cada 90°] R
AB=AC ——————–[dado] S
AD=AD ——–[común] S
∴ ∆BAD ≅∆CAD
BD=DC ————-[cpct]
∴ AD biseca BC
∠1=∠2 ————-[cpct]
∴AD biseca ∠A
Pregunta 3. Dos lados AB y BC y la mediana AM de un triángulo ABC son respectivamente iguales a los lados PQ y QR y la mediana PN de Δ PQR (ver Fig. 7.40). Muestra esa:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ PQR
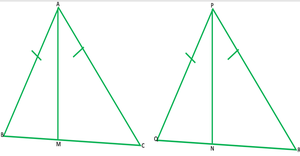
Solución:
Dado:
AB=PQ
BC=QR
AM=PN
AM y PN son medianas
Para mostrar :(i) ΔABM ≅ ΔPQN (ii) ΔABC ≅ PQR
Solución: En ΔABM y ΔPQN
AB=PQ
AM=PN
porque AM y PN son medianas BC=QR
por lo tanto =1/2BC=1/2QR
∴BM=QN
∴) ΔABM ≅ ΔPQN ———[SSS]
∠B=∠Q ——–[cpct]
ii)ahora en ΔABC y ΔPQR
AB=PQ ———-[dado]
∠B=∠Q de (i)
BC=QR —————-[dado]
∴ ΔABC ≅ PQR [SAS]
Pregunta 4. BE y CF son dos alturas iguales de un triángulo ABC. Usando la regla de congruencia RHS, demuestre que el triángulo ABC es isósceles.
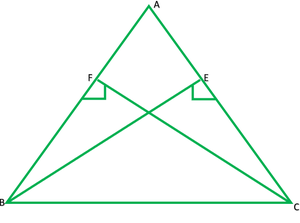
Solución:
Dado: la altitud BE y CF son iguales
Demostrar: ΔABC es un Δ isósceles
En ΔBEC y ΔCEB
∠E=∠F —————-[cada 90°] R
BC=BC —————–[común] H
BF=CF —————-[dado] S
# ΔBEC ≅ ΔCEB [lado derecho]
∠C=∠B ————-[CPCT]
En ΔABC,
∠C=∠B
Pregunta 5. ABC es un triángulo isósceles con AB = AC. Dibuja AP ⊥ BC para mostrar que ∠B = ∠C.
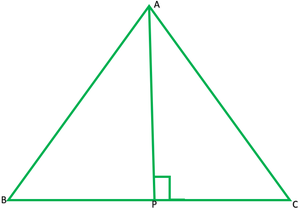
Solución:
Dado:
En ∆ABC,
AB=BC
PA ⊥ BC
para mostrar que: ∠B = ∠C.
Solución:
En ∆APB y ∆APC
∠APB = ∠APC —————[ cada 90°] R
AB=AC ——————-[dado] H
AP=AP ——————–[común] S
∴∆APB ≅ ∆APC ———-[lado derecho]
∠B = ∠C —————[CPCT]
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA