Capítulo 9 Áreas de paralelogramos y triángulos – Ejercicio 9.3 Serie 1
Pregunta 11. En la figura, ABCDE es un pentágono. Una línea a través de B paralela a AC se encuentra con DC producida en F.

Muestra esa
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(AEDF) = ar(ABCDE)
Solución:
(i) ΔACB y ΔACF se encuentran sobre la misma base AC y entre los mismos paralelos AC y BF.
Por lo tanto,
ar(ΔACB) = ar(ΔACF)
(ii) ar(ΔACB) = ar(ΔACF)
=> ar(ΔACB)+ar(ΔACDE) = ar(ΔACF)+ar(ΔACDE)
=> ar(ABCDE) = ar(AEDF)
Pregunta 12. Un aldeano de Itwaari tiene un terreno en forma de cuadrilátero. El Gram Panchayat del pueblo decidió apoderarse de una parte de su terreno de una de las esquinas para construir un Centro de Salud. Itwaari está de acuerdo con la propuesta anterior con la condición de que se le debe dar la misma cantidad de tierra en lugar de su tierra contigua a su parcela para formar una parcela triangular. Explique cómo se implementará esta propuesta.
Solución:

Supongamos que ABCD es la parcela de la tierra de la forma de un cuadrilátero.
Construcción:
Únete a la diagonal BD.
Dibuja AE paralelo a BD.
Únase a BE, que intersecó a AD en O.
Obtendremos,
ΔBCE es la forma del campo original de Itwari
ΔAOB es el área de construcción del Centro de Salud.
ΔDEO es el terreno unido a la parcela.
Probar:
ar(ΔDEO) = ar(ΔAOB)
Prueba:
ΔDEB y ΔDAB se encuentran en la misma base BD, entre los mismos paralelos BD y AE.
Por lo tanto,
Ar(ΔDEB) = ar(ΔDAB)
=> ar(ΔDEB) – ar(ΔDOB) = ar(ΔDAB) – ar(ΔDOB)
=> ar(ΔDEO) = ar(ΔAOB)
Pregunta 13. ABCD es un trapecio con AB || CORRIENTE CONTINUA. Una recta paralela a AC corta a AB en X ya BC en Y. Demuestra que ar (ΔADX) = ar (ΔACY).
[Sugerencia: Únase a CX.]
Solución:

Dado:
ABCD es un trapecio con,
AB || CORRIENTE CONTINUA.
XY || C.A.
Para construir,
Unirse a CX
Demostrar:
ar(ADX) = ar(ACY)
Prueba:
ar(ΔADX) = ar(ΔAXC) -(ecuación 1)(Ya que están en la misma base AX y
entre los mismos paralelos AB y CD)
además,
ar(ΔAXC)=ar(ΔACY) -(ecuación-2)(Dado que están en la misma base AC y
entre los mismos paralelos XY y AC)
De la ecuación (1) y (2),
ar(ΔADX) = ar(ΔACY)
Pregunta 14. En la Figura AP || BQ || CR. Demuestre que ar(ΔAQC) = ar(ΔPBR).
Solución:

Dado:
AP || BQ || CR
Demostrar:
ar(AQC) = ar(PBR)
Prueba:
ar(ΔAQB) = ar(ΔPBQ) -(ecuación 1)(Ya que están en la misma base BQ y
entre los mismos paralelos AP y BQ)
además,
ar(ΔBQC) = ar(ΔBQR) (ecuación 2)(Ya que están en la misma base BQ y
entre los mismos paralelos BQ y CR)
Sumando las ecuaciones (1) y (2),
ar(ΔAQB)+ar(ΔBQC) = ar(ΔPBQ)+ar(ΔBQR)
=> ar(ΔAQC) = ar(ΔPBR)
Pregunta 15. Las diagonales AC y BD de un cuadrilátero ABCD se cortan en O de tal manera que ar(△AOD) = ar(△BOC). Demostrar que ABCD es un trapecio.
Solución:
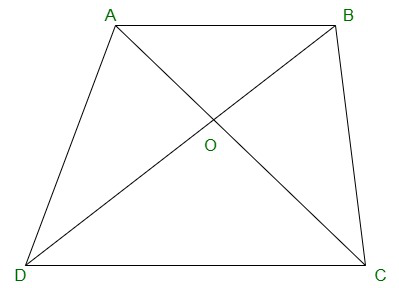
Dado:
ar(ΔAOD) = ar(ΔBOC)
Demostrar:
ABCD es un trapecio.
Prueba:
ar(ΔAOD) = ar(ΔBOC)
=> ar(ΔAOD) + ar(ΔAOB) = ar(ΔBOC)+ar(ΔAOB)
=> ar(ΔADB) = ar(ΔACB)
Las áreas de ΔADB y ΔACB son iguales.
Por lo tanto,
Deben estar entre las mismas líneas paralelas.
Por lo tanto,
AB ∥CD
Por lo tanto, ABCD es un trapecio.
Pregunta 16. En la figura, ar(DRC) = ar(DPC) y ar(BDP) = ar(ARC). Demuestra que los cuadriláteros ABCD y DCPR son trapecios.

Solución:
Dado:
ar(ΔDRC) = ar(ΔDPC)
ar(ΔBDP) = ar(ΔARC)
Demostrar:
ABCD y DCPR son trapecios.
Prueba:
ar(ΔBDP) = ar(ΔARC)
⇒ ar(ΔBDP) – ar(ΔDPC) = ar(ΔDRC)
⇒ ar(ΔBDC) = ar(ΔADC)
ar(ΔBDC) = ar(ΔADC).
Por lo tanto,
ar(ΔBDC) y ar(ΔADC) se encuentran entre las mismas líneas paralelas.
Por lo tanto, AB ∥ CD
ABCD es un trapecio.
Similarmente,
ar(ΔDRC) = ar(ΔDPC).
Por lo tanto,
ar(ΔDRC) y ar(ΔDPC) se encuentran entre las mismas líneas paralelas.
Por lo tanto, DC ∥ PR
Por lo tanto, DCPR es un trapecio.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
