Pregunta 1. En la Figura, E es cualquier punto en la mediana AD de un ΔABC. Demuestre que ar (ABE) = ar (ACE).
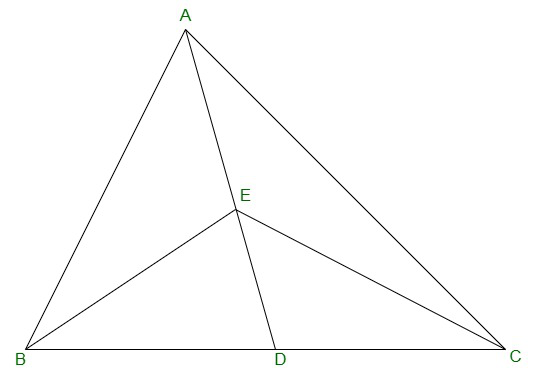
Solución:
Dado:
AD es la mediana de ΔABC.
Por lo tanto,
Dividirá ΔABC en dos triángulos de igual área.
Por lo tanto,
ar(ABD) = ar(ACD) -(ecuación 1)
además,
ED es la mediana de ΔABC.
Por lo tanto,
ar(EBD) = ar(ECD) -(ecuación 2)
Restando la ecuación (2) de (1),
ar(ABD) – ar(EBD) = ar(ACD) – ar(ECD)
=> ar(ABE) = ar(ACE)
Pregunta 2. En un triángulo ABC, E es el punto medio de la mediana AD. Demuestra que ar(BED) = 1/4 ar(ABC).
Solución:
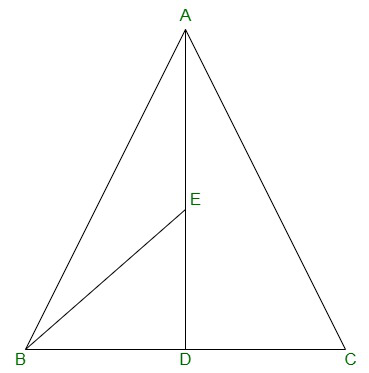
ar(CAMA) = (1/2)×BD×DE
De este modo,
E es el punto medio de AD,
AE = DE
De este modo,
AD es la mediana del lado BC del triángulo ABC,
BD = CC
DE = (1/2) AD -(ecuación 1)
BD = (1/2)BC -(ecuación-2)
De la ecuación (1) y (2), obtenemos,
ar(CAMA) = (1/2) × (1/2)BC × (1/2)AD
=> ar(CAMA) = (1/2) × (1/2)ar(ABC)
=> ar(CAMA) = 1/4 ar(ABC)
Pregunta 3. Demuestra que las diagonales de un paralelogramo lo dividen en cuatro triángulos de igual área.
Solución:
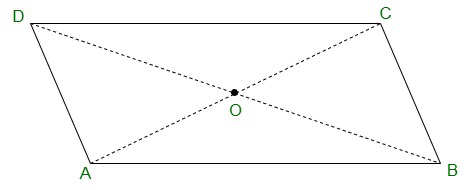
O es el punto medio de AC y BD. (como las diagonales se bisecan entre sí)
En ΔABC, BO es la mediana.
Por lo tanto,
ar(AOB) = ar(BOC) -(ecuación 1)
además,
En ΔBCD, CO es la mediana.
Por lo tanto,
ar(BOC) = ar(COD) -(ecuación 2)
En ΔACD, OD es la mediana.
Por lo tanto,
ar(AOD) = ar(COD) -(ecuación 3)
En ΔABD, AO es la mediana.
Por lo tanto,
ar(AOD) = ar(AOB). -(ecuación4)
De las ecuaciones (1), (2), (3) y (4), tenemos,
ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)
Por lo tanto,
obtenemos, las diagonales de un paralelogramo lo dividen en cuatro triángulos de igual área.
Pregunta 4. En la figura, ABC y ABD son dos triángulos en la misma base AB. Si el segmento de línea CD es bisecado por AB en O, demuestre que: ar(ABC) = ar(ABD).
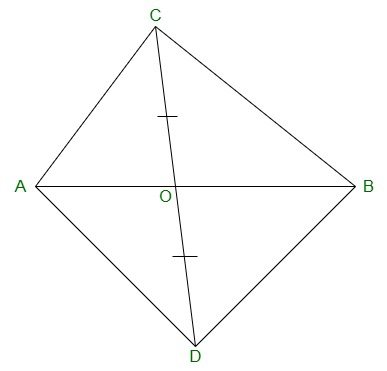
Solución:
En ΔABC, AO es la mediana. (CD es atravesado por AB en O)
Por lo tanto,
ar(AOC) = ar(AOD) -(ecuación 1)
además,
ΔBCD, BO es la mediana. (CD es atravesado por AB en O)
Por lo tanto,
ar(BOC) = ar(DBO) -(ecuación 2)
Sumando la ecuación (1) y (2),
Obtendremos,
ar(AOC)+ar(BOC) = ar(AOD)+ar(DBO)
=> ar(ABC) = ar(ABD)
Pregunta 5. D, E y F son respectivamente los puntos medios de los lados BC, CA y AB de un ΔABC. Muestra esa
(i) BDEF es un paralelogramo.
(ii) ar(DEF) = 1/4 ar(ABC)
(iii) ar (BDEF) = 1/2 ar (ABC)
Solución:
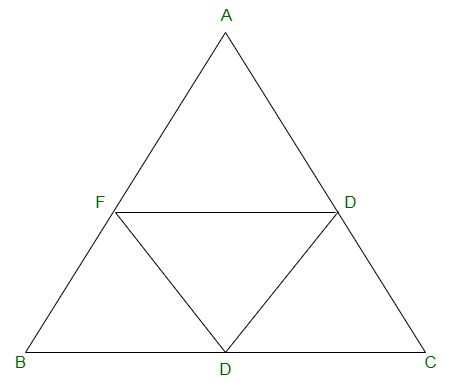
(i) En ΔABC,
FE || BC y EF = 1/2 BC (por el teorema del punto medio)
además,
BD = 1/2 BC (D es el punto medio)
Asi que,
BD = FE
además,
BF y DE son paralelos e iguales entre sí.
Por lo tanto,
Los dos lados opuestos tienen la misma longitud y son paralelos entre sí.
Por lo tanto, BDEF es un paralelogramo.
(ii) Partiendo del resultado de (i),
BDEF, DCEF, AFDE son paralelogramos.
La diagonal de un paralelogramo lo divide en dos triángulos de igual área.
Por lo tanto,
ar(ΔBFD) = ar(ΔDEF) (Para paralelogramo BDEF) -(ecuación 1)
además,
ar(ΔAFE) = ar(ΔDEF) (Para paralelogramo DCEF) -(ecuación 2)
ar(ΔCDE) = ar(ΔDEF) (Para paralelogramo AFDE) -(ecuación 3)
De las ecuaciones (1), (2) y (3)
ar(ΔBFD) = ar(ΔAFE) = ar(ΔCDE) = ar(ΔDEF)
=> ar(ΔBFD) + ar(ΔAFE) + ar(ΔCDE) + ar(ΔDEF) = ar(ΔABC)
=> 4 ar(ΔDEF) = ar(ΔABC)
=> ar(DEF) = 1/4 ar(ABC)
(iii) Área (paralelogramo BDEF) = ar(ΔDEF) + ar(ΔBDE)
=> ar(paralelogramo BDEF) = ar(ΔDEF) + ar(ΔDEF)
=> ar(paralelogramo BDEF) = 2× ar(ΔDEF)
=> ar(paralelogramo BDEF) = 2× 1/4 ar(ΔABC)
=> ar(paralelogramo BDEF) = 1/2 ar(ΔABC)
Pregunta 6. En la figura, las diagonales AC y BD del cuadrilátero ABCD se intersecan en O de manera que OB = OD.
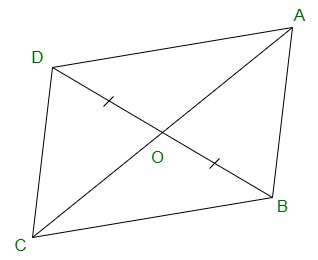
Si AB = CD, entonces demuestre que:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) AD || CB o ABCD es un paralelogramo.
[Sugerencia: desde D y B, dibuje perpendiculares a AC.]
Solución:
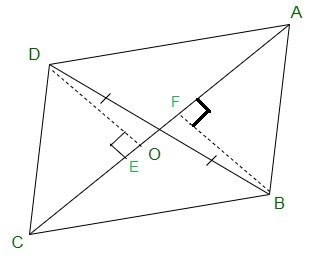
Dado:
OB = OD y AB = CD
Construir,
DE ⊥ AC y BF ⊥ AC.
A prueba:
(i) En ΔDOE y ΔBOF,
∠DEO = ∠BFO (Perpendiculares)
∠DOE = ∠BOF (Ángulos verticalmente opuestos)
OD = OB (Dado)
Por lo tanto,
ΔDOE ≅ ΔBOF por condición de congruencia AAS.
Por lo tanto, DE = BF (Por CPCT) – (ecuación 1)
además,
ar(ΔDOE) = ar(ΔBOF) (Triángulos congruentes) -(ecuación 2)
Ahora,
En ΔDEC y ΔBFA,
∠DEC = ∠BFA (ya que son perpendiculares)
CD = AB (Dado)
DE = BF (De la ecuación 1)
Por lo tanto,
ΔDEC ≅ ΔBFA por condición de congruencia RHS.
Por lo tanto,
ar(ΔDEC) = ar(ΔBFA) (Triángulos congruentes) -(ecuación 3)
Sumando la ecuación (2) y (3),
ar(ΔDOE) + ar(ΔDEC) = ar(ΔBOF) + ar(ΔBFA)
=> ar (DOC) = ar (AOB)
(ii) ar(ΔDOC) = ar(ΔAOB)
Sumando ar(ΔOCB) en LHS y RHS,
obtendremos,
=> ar(ΔDOC) + ar(ΔOCB) = ar(ΔAOB) + ar(ΔOCB)
=> ar(ΔDCB) = ar(ΔACB)
(iii) Cuando dos triángulos tienen la misma base y áreas iguales,
los triángulos estarán entre las mismas líneas paralelas
ar(ΔDCB) = ar(ΔACB)
AD || BC -(ecuación 4)
Para el cuadrilátero ABCD, un par de lados opuestos son
iguales (AB = CD) y otro par de lados opuestos son paralelos.
Por lo tanto,
ABCD es paralelogramo.
Pregunta 7. D y E son puntos en los lados AB y AC, respectivamente de ΔABC tales que ar(DBC) = ar(EBC). Demostrar que DE || ANTES DE CRISTO.
Solución:
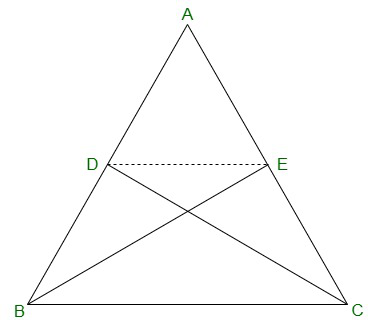
ΔDBC y ΔEBC están en la misma base BC y tienen áreas iguales.
Por lo tanto,
Estarán entre las mismas líneas paralelas.
Por lo tanto,
ES || ANTES DE CRISTO.
Pregunta 8. XY es una línea paralela al lado BC de un triángulo ABC. Si SER || AC y FC || AB se encuentra con XY en E y F respectivamente, muestra que ar(ΔABE) = ar(ΔACF)
Solución:
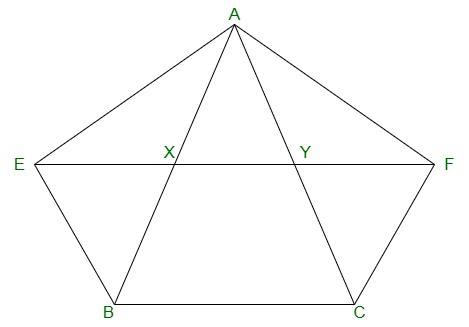
Dado,
XY || BC, SER || AC y FC || AB
Tenemos que demostrar que,
ar(ΔABE) = ar(ΔAC)
Prueba:
BCYE es un paralelogramo ya que ΔABE y ||gm BCYE están en el mismo
base BE y entre las mismas paralelas BE y AC.
Por lo tanto,
ar(ABE) = 1/2 ar(BCYE) -(ecuación 1)
Ahora,
FC || AB y XY || antes de Cristo
=> FC || AB y XF || antes de Cristo
=> BCFX es un paralelogramo.
Por lo tanto, ΔACF y el paralelogramo BCFX están en la misma base CF
y entre los mismos paralelos AB y FC. Por lo tanto,
ar (ΔACF)= 1/2 ar (BCFX) -(ecuación 2)
Pero,
El paralelogramo BCFX y el paralelogramo BCYE están en el mismo
base BC y entre los mismos paralelos BC y EF. Por lo tanto,
ar (BCFX) = ar(BCYE) -(ecuación 3)
De las ecuaciones (1), (2) y (3),
Obtendremos,
ar (ΔABE) = ar(ΔACF)
=> ar(BEYC) = ar(BXFC)
Como los paralelogramos están en la misma base BC y
entre los mismos paralelos EF y BC – (ecuación 3)
También,
ΔAEB y el paralelogramo BEYC están en la misma base
BE y entre los mismos paralelos BE y AC.
=> ar(ΔAEB) = 1/2 ar(BEYC) -(ecuación 4)
Similarmente,
ΔACF y paralelogramo BXFC en la misma base CF
y entre los mismos paralelos CF y AB.
=> ar(ΔACF) = 1/2 ar(BXFC) -(ecuación 5)
De las ecuaciones (3), (4) y (5),
ar(ΔABE) = ar(ΔACF).
Pregunta 9. El lado AB de un paralelogramo ABCD se produce en cualquier punto P. Una línea que pasa por A y es paralela a CP se encuentra con CB en Q y luego se completa el paralelogramo PBQR (ver Figura). Muestra esa
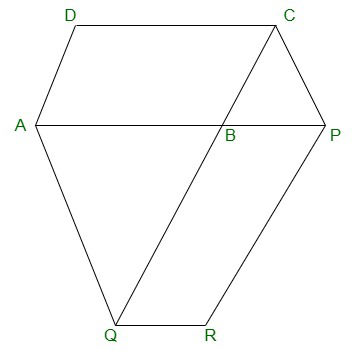
ar(ABCD) = ar(PBQR).
[Sugerencia: únase a AC y PQ. Ahora compare ar(ACQ) y ar(APQ).]
Solución:
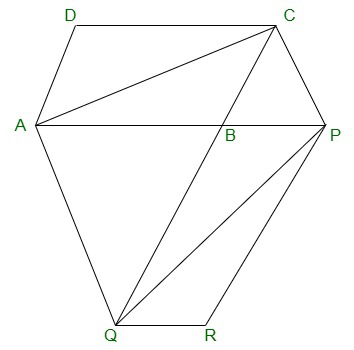
AC y PQ están unidos.
Ar(ΔACQ) = ar(ΔAPQ)(Sobre la misma base AQ y entre
las mismas paralelas AQ y CP)
=> ar(ΔACQ)-ar(ΔABQ) = ar(ΔAPQ)-ar(ΔABQ)
=> ar(△ABC) = ar(△QBP) -(ecuación 1)
AC y QP son las diagonales ABCD y PBQR.
Por lo tanto,
ar(ABC) = 1/2ar(ABCD) -(ecuación 2)
ar(QBP) = 1/2 ar(PBQR) -(ecuación 3)
De la ecuación (2) y (3),
1/2 ar(ABCD) = 1/2 ar(PBQR)
=> ar(ABCD) = ar(PBQR)
Pregunta 10. Diagonales AC y BD de un trapecio ABCD con AB || DC se intersecan en O. Demuestra que ar (AOD) = ar (BOC).
Solución:
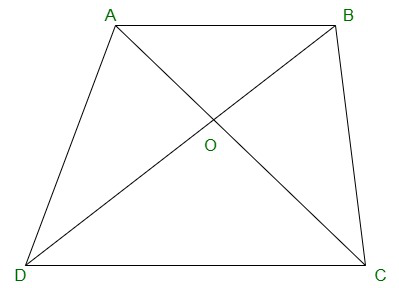
ΔDAC y ΔDBC se encuentran en la misma base DC y
entre los mismos paralelos AB y CD.
Ar(ΔDAC) = ar(ΔDBC)
=> ar(ΔDAC) – ar(ΔDOC) = ar(ΔDBC) – ar(ΔDOC)
=> ar(ΔAOD) = ar(ΔBOC)
Capítulo 9 Áreas de paralelogramos y triángulos – Ejercicio 9.3 | conjunto 2
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA