Clase 10 Soluciones NCERT – Capítulo 14 Estadísticas – Ejercicio 14.3

Pregunta 1. La siguiente distribución de frecuencia da el consumo mensual de electricidad de 68 consumidores en una localidad. Encuentra la mediana, la media y la moda de los datos y compáralos.

Consumo mensual (en unidades)	Nº de clientes
65-85	4
85-105	5
105-125	13
125-145	20
145-165	14
165-185	8
185-205	4

Solución:

Número total de consumidores n = 68

n/2 =34

Entonces, la clase mediana es 125-145 con frecuencia acumulada = 42

Aquí, l = 125, n = 68, C _f = 22, f = 20, h = 20

Ahora encontramos la mediana:

mediana = $l +\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

$=125+\frac{(34−22)}{20} × 20$

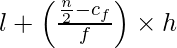
= 125 + 12 = 137

Por lo tanto, la mediana es 137

Ahora encontramos la moda:

Clase modal = 125 – 145,

Las frecuencias son

f ₁ = 20, f ₀ = 13, f ₂ = 14 y h = 20

Modo = $l+ \left[\frac{(f1-f0)}{(2f1-f0-f2)}\right]×h$

Al sustituir los valores en la fórmula dada, obtenemos

Modo = $125 + \frac{(20-13)}{(40-13-14)}×20$

= 125 + 140/13

= 125 + 10,77

= 135,77

Por lo tanto, la moda es 135.77

Ahora encontramos la media:

Intervalo de clases yo _{_} x _yo re _yo = x _yo – un tu _yo = re _yo / h si _yo_tu yo

65-85 4 75 -60 -3 -12

85-105 5 95 -40 -2 -10

105-125 13 115 -20 -1 -13

125-145 20 135 0 0 0

145-165 14 155 20 1 14

165-185 8 175 40 2 dieciséis

185-205 4 195 60 3 12

Suma f _i = 68 Suma f _yo tu _yo = 7

$\bar{x} =a+h \frac{∑f_iu_i}{∑f_i}$

= 135 + 20(7/68)

= 137,05

Por lo tanto, la media es 137.05

Ahora, al comparar la mediana, la media y la moda, encontramos que la media, la mediana y la moda son más o menos iguales en esta distribución.

Pregunta 2. Si la mediana de una distribución dada a continuación es 28.5, encuentre el valor de x e y.

Intervalo de clases	Frecuencia
0-10	5
10-20	X
20-30	20
30-40	15
40-50	y
50-60	5
Total	60

Solución:

Según la pregunta

El número total de observaciones es n = 60

Mediana de los datos dados = 28.5

n/2 = 30

La clase media es 20 – 30 con una frecuencia acumulada = 25 + x

Límite inferior de la clase mediana, l = 20,

dof ₌ 5 + x,

f = 20 y h = 10

Ahora encontramos la mediana:

mediana = $l+\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

28,5 = $20+\frac{(30−5−x)}{20} × 10$

8.5 = (25 – x)/2

17 = 25 – x

Por lo tanto, x = 8

A partir de la frecuencia acumulada, podemos identificar el valor de x + y de la siguiente manera:

60 = 5 + 20 + 15 + 5 + x + y

Al sustituir los valores de x, encontraremos el valor de y

60 = 5 + 20 + 15 + 5 + 8 + y

y = 60 – 53

y = 7

Entonces el valor de a es 8 y y es 7

Pregunta 3. El agente de seguros de Vida encontró los siguientes datos para la distribución de edades de 100 asegurados. Calcule la mediana de edad, si las pólizas se otorgan solo a las personas cuya edad es de 18 años en adelante pero menor de 60 años.

Edad en años)	Número de titular de la póliza
Por debajo de 20	2
Por debajo de 25	6
Por debajo de 30	24
Por debajo de 35	45
Por debajo de 40	78
Por debajo de 45	89
Por debajo de 50	92
Por debajo de 55	98
Por debajo de 60	100

Solución:

De acuerdo con la pregunta dada, la tabla es

Intervalo de clases Frecuencia Frecuencia acumulada

15-20 2 2

20-25 4 6

25-30 18 24

30-35 21 45

35-40 33 78

40-45 11 89

45-50 3 92

50-55 6 98

55-60 2 100

Datos dados: n = 100 y n/2 = 50

Clase mediana = 35 – 45

Entonces, l = 35, c _f = 45, f = 33 y h = 5

Ahora encontramos la mediana:

mediana = $l+\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

mediana = $35+\frac{(50-45)}{33} × 5$

= 35 + 5(5/33)

= 35,75

Por lo tanto, la mediana de edad es de 35,75 años.

Pregunta 4. Las longitudes de 40 hojas en una planta se miden correctamente al milímetro más cercano, y los datos obtenidos se representan como en la siguiente tabla:

Longitud (en mm)	Número de hojas
118-126	3
127-135	5
136-144	9
145-153	12
154-162	5
163-171	4
172-180	2

Encuentra la mediana de la longitud de las hojas.

Solución:

Los datos en la tabla dada no son continuos para reducir 0.5 en el límite inferior y agregar 0.5 en el límite superior.

Obtenemos una nueva tabla:

Intervalo de clases Frecuencia Frecuencia acumulada

117,5-126,5 3 3

126,5-135,5 5 8

135,5-144,5 9 17

144,5-153,5 12 29

153,5-162,5 5 34

162,5-171,5 4 38

171,5-180,5 2 40

De la tabla dada

n = 40 y n/2 = 20

Clase mediana = 144,5 – 153,5

l = 144,5,

cf = 17, f = 12 y h = 9

Ahora encontramos la mediana:

mediana = $l+\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

mediana = $144.5+\frac{(20-17)}{12}×9$

= 144,5 + 9/4

= 146,75 mm

Por tanto, la mediana de la longitud de las hojas es de 146,75 mm.

Pregunta 5. La siguiente tabla muestra la distribución del tiempo de vida de 400 lámparas de neón.

Vida útil (en horas)	Número de lámparas
1500-2000	14
2000-2500	56
2500-3000	60
3000-3500	86
3500-4000	74
4000-4500	62
4500-5000	48

Encuentre la vida media de una lámpara.

Solución:

Según la pregunta

Intervalo de clases Frecuencia Acumulativo

1500-2000 14 14

2000-2500 56 70

2500-3000 60 130

3000-3500 86 216

3500-4000 74 290

4000-4500 62 352

4500-5000 48 400

n = 400 y n/2 = 200

Clase mediana = 3000 – 3500

l = 3000, C _f = 130,

f = 86 y h = 500

Ahora encontramos la mediana:

mediana = $l+\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

mediana = $3000 + \frac{(200-130)}{86} × 500$

= 3000 + 35000/86 = 3000 + 406,97

= 3406.97

Por lo tanto, la vida media de las lámparas es de 3406,97 horas.

Pregunta 6. En esta se tomaron al azar 100 apellidos de un directorio telefónico local y se obtuvo la distribución de frecuencias del número de letras en alfabetos ingleses en los apellidos de la siguiente manera:

Número de letras	1-4	4-7	7-10	10-13	13-16	16-19
Número de apellidos	6	30	40	dieciséis	4	4

Determine el número de letras medianas en los apellidos. Encuentre el número de letras medias en los apellidos y también, encuentre el tamaño de modal en los apellidos.

Solución:

Según la pregunta

Intervalo de clases Frecuencia Frecuencia acumulada

1-4 6 6

4-7 30 36

7-10 40 76

10-13 dieciséis 92

13-16 4 96

16-19 4 100

n = 100 y n/2 = 50

Clase mediana = 7 – 10

Por lo tanto, l = 7, C _f = 36, f = 40 & h = 3

Ahora encontramos la mediana:

mediana = $l+\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

mediana = $7+\frac{(50-36)}{40} × 3$

Mediana = 7 + 42/40 = 8,05

Por lo tanto, la mediana es 8.05

Ahora encontramos la moda:

Clase modal = 7 – 10,

Donde, l = 7, f ₁ = 40, f ₀ = 30, f ₂ = 16 y h = 3

Modo = $l+\left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

Modo = $7+\frac{(40-30)}{(2×40-30-16)} × 3$

= 7 + 30/34 = 7,88

Por lo tanto, la moda es 7.88

Ahora encontramos la media:

Intervalo de clases yo _{_} x _yo arreglar _yo x _yo

1-4 6 2.5 15

4-7 30 5.5 165

7-10 40 8.5 340

10-13 dieciséis 11.5 184

13-16 4 14.5 51

16-19 4 17.5 70

Suma f _i = 100 Suma f _yo x _yo = 825

Media = $\bar{x}= \frac{∑f_i x_i }{∑f_i}$

= 825/100 = 8,25

Por lo tanto, la media es 8.25

Pregunta 7. Las distribuciones de abajo dan un peso de 30 estudiantes de una clase. Encuentre la mediana del peso de un estudiante.

Peso (en kg)	40-45	45-50	50-55	55-60	60-65	65-70	70-75
Numero de estudiantes	2	3	8	6	6	3	2

Solución:

Según la pregunta

Intervalo de clases Frecuencia Frecuencia acumulada

40-45 2 2

45-50 3 5

50-55 8 13

55-60 6 19

60-65 6 25

65-70 3 28

70-75 2 30

n = 30 y n/2 = 15

Clase mediana = 55 – 60

l = 55, C _f = 13, f = 6 y h = 5

Ahora encontramos la mediana:

mediana = $l +\left(\frac{\frac{n}{2}-c_f}{f}\right)\times h$

Al sustituir los valores en la fórmula dada, obtenemos

mediana = $55+\frac{(15-13)}{6}×5$

= 55 + 10/6 = 55 + 1,666

= 56,67

Por lo tanto, el peso mediano de los estudiantes es 56.67

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. La siguiente distribución de frecuencia da el consumo mensual de electricidad de 68 consumidores en una localidad. Encuentra la mediana, la media y la moda de los datos y compáralos.

Pregunta 2. Si la mediana de una distribución dada a continuación es 28.5, encuentre el valor de x e y.

Pregunta 3. El agente de seguros de Vida encontró los siguientes datos para la distribución de edades de 100 asegurados. Calcule la mediana de edad, si las pólizas se otorgan solo a las personas cuya edad es de 18 años en adelante pero menor de 60 años.

Pregunta 4. Las longitudes de 40 hojas en una planta se miden correctamente al milímetro más cercano, y los datos obtenidos se representan como en la siguiente tabla:

Encuentra la mediana de la longitud de las hojas.

Pregunta 5. La siguiente tabla muestra la distribución del tiempo de vida de 400 lámparas de neón.

Encuentre la vida media de una lámpara.

Pregunta 6. En esta se tomaron al azar 100 apellidos de un directorio telefónico local y se obtuvo la distribución de frecuencias del número de letras en alfabetos ingleses en los apellidos de la siguiente manera:

Determine el número de letras medianas en los apellidos. Encuentre el número de letras medias en los apellidos y también, encuentre el tamaño de modal en los apellidos.

Pregunta 7. Las distribuciones de abajo dan un peso de 30 estudiantes de una clase. Encuentre la mediana del peso de un estudiante.

Deja una respuesta Cancelar la respuesta