Pregunta 1. Realice las siguientes divisiones.
(yo) 28x 4 ÷ 56x
Solución:
28x 4 = 2 × 2 × 7 × x × x × x × x
56x = 2 × 2 × 2 × 7 × x
28x 4 ÷ 56x =
(agrupando 28x para cancelar)
= ½ × x × x × x
= ½ x 3
(ii) -36y 3 ÷ 9y 2
Solución:
-36y 3 = -2 × 2 × 3 × 3 × y × y × y
9y 2 = 3 × 3 × y × y
-36y 3 ÷ 9y 2 =
(agrupando 9y 2 para cancelar)
= -(2 × 2 × y)
= -4 años
(iii) 66pq 2 r 3 ÷ 11qr 2
Solución:
66pq 2 r 3 = 2 × 3 × 11 × p × q × q × r × r × r
11qr 2 = 11 × q × r × r
66pq 2 r 3 ÷ 11qr 2 =
(agrupando 11qr 2 para cancelar)
= (2 × 3 × p × q × r)
= 6pqr
(iv) 34x 3 y 3 z 3 ÷ 51xy 2 z 3
Solución:
34x 3 y 3 z 3 = 2 × 17 × x × x × x × y × y × y × z × z × z
51xy 2 z 3 = 3 × 17 × x × y × y × z × z × z
34x 3 y 3 z 3 ÷ 51xy 2 z 3 =

=
(agrupando 17xy 2 z 3 para cancelar)
=
x 2 y
(v) 12a 8 b 8 ÷ (-6a 6 b 4 )
Solución:
12a 8 b 8 = 2 × 2 × 3 × a × a × a × a × a × a × a × a × b × b × b × b × b × b × b × b
-6a 6 b 4 = -2 × 3 × a × a × a × a × a × a × b × b × b × b
12a 8 segundo 8 ÷ (-6a 6 segundo 4 ) =
= – (2 × a × a × b × b × b × b) (agrupando 6a 6 b 4 para cancelar)
= -2a 2 b 4
Pregunta 2. Divide el polinomio dado por el monomio dado.
(i) (5x 2 – 6x) ÷ 3x
Solución:
5x 2 – 6x = (5 × x × x) – (2 × 3 × x)
= 5x × (x) – 6 × (x)
= x(5x – 6)
3x = 3 × (x)
(5x 2 – 6x) ÷ 3x =
(agrupando x para cancelar)
=
(ii) (3y 8 – 4y 6 + 5y 4 ) ÷ y 4
Solución:
3y 8 -4y 6 +5y 4 = y 4 [(3 × y × y × y × y) – (2× 2 × y × y) + (5)]
y 4 = (y × y × y × y)
(3y 8 -4y 6 +5y 4 ) ÷ y 4 =
(agrupando y 4 para cancelar)
= (3x 4 -4y 2 +5 )
(iii) 8(x 3 y 2 z 2 + x 2 y 3 z 2 + x 2 y 2 z 3 ) ÷ 4x 2 y 2 z 2
Solución:
8 (x 3 y 2 z 2 + x 2 y 3 z 2 + x 2 y 2 z 3 ) = 2 × 2 × 2 × x 2 y 2 z 2 (x + y + z)
4 xx 2 y 2 z 2 = 2 × 2 × x 2 y 2 z 2
8(x 3 y 2 z 2 + x 2 y 3 z 2 + x 2 y 2 z 3 ) ÷ 4x 2 y 2 z 2 =
(agrupar x 2 y 2 z 2 para cancelar)
= 2(x+y+z)
(iv) (x 3 +2x 2 +3x) ÷ 2x
Solución:
x3 +2×2 +3x = x × (x2 + 2x + 3 )
(x 3 +2x 2 +3x) ÷ 2x =
(agrupando x para cancelar)
=
(v) (p 3 q 6 -p 6 q 3 ) ÷ p 3 q 3
Solución:
p 3 q 6 -p 6 q 3 = p 3 q 3 (q 3 -p 3 )
(p 3 q 6 -p 6 q 3 ) ÷ p 3 q 3 =
(agrupar p 3 q 3 para cancelar)
= q 3 – p 3
Pregunta 3. Resuelve las siguientes divisiones.
(yo) (10x – 25) ÷ 5
Solución:
10x-25 = (5 × 2 × x) – (5 × 5)
= 5(2x-5)
(10x-25) ÷ 5 =
(agrupar 5 para cancelar)
= (2x – 5)
(ii) (10x – 25) ÷ (2x – 5)
Solución:
10x-25 = 5(2x-5)
(10x-25)÷(2x-5) =
(agrupando (2x-5) para cancelar)
= 5
(iii) 10y(6y+21) ÷ 5(2y+7)
Solución:
10y(6y+21) = 5 × 2 × y × 3 × (2y+7)
10y(6y+21) ÷ 5(2y+7) =
(agrupando 5(2y+7) para cancelar)
= 2 × 3 × y
= 6 años
(iv) 9x 2 y 2 (3z-24) ÷ 27xy(z-8)
Solución:
9x 2 y 2 (3z-24) = 3 × 3 × x 2 × y 2 × 3 × (z-8)
27xy(z-8) = 3 × 3 × 3 × x × y × (z-8)
9x 2 y 2 (3z-24)÷27xy(z-8)=
(agrupando (27xy(z-8)) para cancelar)
= xy
(v) 96abc(3a-12)(5b-30) ÷ 144 (a-4)(b-6)
Solución:
96abc(3a-12)(5b-30) = 2 × 2 × 2 × 2 × 2 × 3 × a × b × c × 3 × (a-4) × 5 × (b-6)
144(a-4)(b-6) = 2 × 2 × 2 × 2 × 3 × 3 × (a-4) × (b-6)
96abc(3a-12)(5b-30) ÷ 144(a-4)(b-6) =
= (2 × 5 × a × b × c) (agrupando (144(a-4)(b-6)) para cancelar)
= 10abc
Pregunta 4. Divida como se indica.
(i) 5(2x+1)(3x+5) ÷ (2x+1)
Solución:
= 5(3x+1) (agrupando (2x+1) para cancelar)
(ii) 26xy(x+5)(y-4)÷13x(y-4)
Solución:
26xy(x+5)(y-4) = 2 × 13 × x × y × (x+5) × (y-4)
26xy(x+5)(y-4)÷13x(y-4) =
(agrupando 13x(y-4) para cancelar)
= (2 × y × (x+5))
= 2y(x+5)
(iii) 52pqr(p+q)(q+r)(r+p)÷104pq(q+r)(r+p)
Solución:
52pqr(p+q)(q+r)(r+p) = 13 × 2 × 2 × pqr(p+q)(q+r)(r+p)
104pq(q+r)(r+p) = 13 × 2 × 2 × 2 × pq(q+r)(r+p)
52pqr(p+q)(q+r)(r+p)÷104pq(q+r)(r+p) =
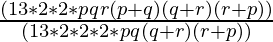
=
(agrupando (52pq(q+r)(r+p)) para cancelar)
(iv) 20(y+4)( y2 +5y+3)÷5(y+4)
Solución:
20(y+4)(y 2 +5y+3) = 2 × 2 × 5 × (y+4) × (y 2 +5y+3)
20(y+4)(y 2 +5y+3)÷5(y+4) =
(agrupando (5(y+4)) para cancelar)
= 2 × 2 × ( y2 +5y+3)
= 4( y2 +5y+3)
(v) x(x+1)(x+2)(x+3) ÷ x(x+1)
Solución:
= (x+2)(x+3) (agrupando x(x+1) para cancelar)
Pregunta 5. Factoriza las expresiones y divídelas como se indica.
(i) (y 2 +7y+10) ÷ (y+5)
Solución:
( y2 +7y+10) = ( y2 +5y+2y+10)
= (y(y+5) + 2(y+5)) (2 + 5 = 7 y 2 × 5 = 10)
= (y+5) (y+2)
(y 2 +7y+10) ÷ (y+5) =
(agrupando (y+5) para cancelar)
= (y+2)
(ii) (m 2 -14m-32) ÷ (m+2)
Solución:
(m2 -14m -32) = (m2 -16m+ 2m -32 )
= (m(m-16) + 2(m-16)) (-16 + 2 = -14 & -16 × 2 = -32)
= (m+2) (m-16)
(m 2 -14m-32)÷(m+2) =
(agrupando (m+2) a cancelar)
= (m-16)
(iii) (5p 2 -25p+20) ÷ (p-1)
Solución:
(5p 2 -25p+20) = (5p 2 -20p-5p+20)
=(5p(p-4)-5(p-4)) (-20 – 5 = -25 )
=(5p-5) (p-4)
=5 (p-1) (p-4)
(5p 2 -25p+20) ÷ (p-1) =
(agrupación (p-1) para cancelar)
= 5(p-4)
(iv) 4yz(z 2 +6z-16)÷2y(z+8)
Solución:
4yz(z 2 +6z-16) = 2 × 2 × y × z × (z 2 +8z-2z-16)
= 2 × 2 × y × z × (z(z+8)-2(z+8)) (8 + (-2) = 6 y 8 × (-2) = -16)
= 2 × 2 × y × z × (z+8) (z-2))
4yz(z 2 +6z-16) ÷ 2y(z+8) =
(agrupando 2y(z+8) para cancelar)
= 2 × z × (z-2)
= 2z(z-2)
(v) 5pq(p 2 -q 2 )÷2p(p+q)
Solución:
(p 2 -q 2 ) = (p+q) (pq) (IDENTIDAD a 2 -b 2 = (a+b)(ab) )
5pq(p 2 -q 2 )÷2p(p+q) =
(agrupando p(p+q) para cancelar)
=
(vi) 12xy(9x 2 -16y 2 ) ÷ 4xy(3x+4y)
soln.
12xy(9x 2 -16y 2 ) = 2 × 2 × 3 × ((3x) 2 -(4y) 2 )
12xy(9x 2 -16y 2 ) = 2 × 2 × 3 × (3x+4y) (3x-4y) (IDENTIDAD a 2 -b 2 = (a+b)(ab) )
12xy(9x 2 -16y 2 ) ÷ 4xy(3x+4y) =
(agrupando 4xy(3x+4y) para cancelar)
= 3 (3x-4y)
(vii) 39y 3 (50y 2 -98) ÷ 26y 2 (5y+7)
Solución:
39y 3 (50y 2 -98) = 3 × 13 × y 3 × 2 × (25y 2 -49)
= 3 × 13 × y 3 × 2 × ((5y) 2 -(7) 2 ) (IDENTIDAD a 2 -b 2 = (a+b)(ab) )
= 3 × 13 × y 3 × 2 × (5y+7) (5y-7)
26y 2 (5y+7) = 2 × 13 × y 2 × (5y+7)
39y 3 (50y 2 -98)÷26y 2 (5y+7) =
(agrupando 26y 2 (5y+7) para cancelar)
= (3 × y × (5y-7))
= 3y(5y-7)