Pregunta 1: Clasifica los siguientes números como racionales o irracionales:
(i) 2 –√5
(ii) (3 +√23)- √23
(iii) 2√7 / 7√7
(iv) 1/√2
(v) 2π
Solución:
(i) 2 –√5
Como √5 = 2.2360678… que es no terminante y no recurrente. Es un número irracional.
Cuando sustituimos el valor de √5 en la ecuación 2 –√5, obtenemos,
2-√5 = 2-2.2360678…
2-√5 = -0.2360678
Dado que el número, – 0.2360678…, es un número no terminado y no recurrente,
Por lo tanto, 2 –√5 es un número irracional.
(ii) (3 +√23)- √23
(3 +√23) –√23 = 3+√23–√23
= 3
ya que el numero 3 es un numero racional
Por lo tanto, (3 +√23)- √23 es racional.
(iii) 2√7 / 7√7
2√7 / 7√7 = (2/7)× (√7/√7)
2√7 / 7√7 = (2/7)× (√7/√7)
= (2/7)×1 [Como (√7/√7) = 1]
= 2/7
Dado que el número, 2/7 está en forma p/q
Por lo tanto, 2√7/7√7 es racional.
(iv) 1/√2
Como, √2 = 1.41421… que es no terminante y no recurrente. Es un número racional.
Cuando dividimos 1/√2 obtenemos,
1/√2 = 1/1,41421…
=0.70710…
Dado que el número, 0.7071..es un número no terminado y no recurrente,
Por lo tanto, 1/√2 es un número irracional.
(v) 2π
El valor de π es 3.1415…
Cuando sustituimos el valor de π en la ecuación 2π, obtenemos,
2π = 2 × 3,1415… = 6,2831…
Dado que el número, 6.2831…, no es recurrente, no termina,
Por lo tanto, 2π es un número irracional.
Pregunta 2: Simplifica cada una de las siguientes expresiones:
(i) (3+√3)(2+√2)
(ii) (3+√3)(3-√3)
(iii) (√5+√2) 2
(iv) (√5-√2)(√5+√2)
Solución:
(i) (3+√3)(2+√2)
Después de abrir los paréntesis, obtenemos,
(3+√3)(2+√2)= (3×2)+(3×√2)+(√3×2)+(√3×√2)
(3+√3)(2+√2) = 6+3√2+2√3+√6
(ii) (3+√3)(3-√3)
Después de abrir los paréntesis, obtenemos,
(3+√3)(3-√3) = 3 2 -(√3) 2
= 9-3
(3+√3)(3-√3) = 6
(iii) (√5+√2) 2
Después de abrir los paréntesis, obtenemos,
(√5+√2) 2 = √5 2 +(2×√5×√2)+ √2 2 [Usando la fórmula (a + b) 2 = a 2 + 2ab + b 2 ]
= 5+2×√10+2
(√5+√2) 2 = 7+2√10
(iv) (√5-√2)(√5+√2)
Después de abrir los paréntesis, obtenemos,
(√5-√2)(√5+√2) = (√5 2 -√2 2 )
= 5-2
= 3
Pregunta 3: Recuerde, π se define como la relación entre la circunferencia (digamos c) de un círculo y su diámetro (digamos d). Es decir, π =c/d. Esto parece contradecir el hecho de que π es irracional. ¿Cómo resolverá esta contradicción?
Solución:
Dado π = c/d = 22/7 que es igual a 3.142… que es un decimal no recurrente no terminado.
Por lo tanto, π es irracional.
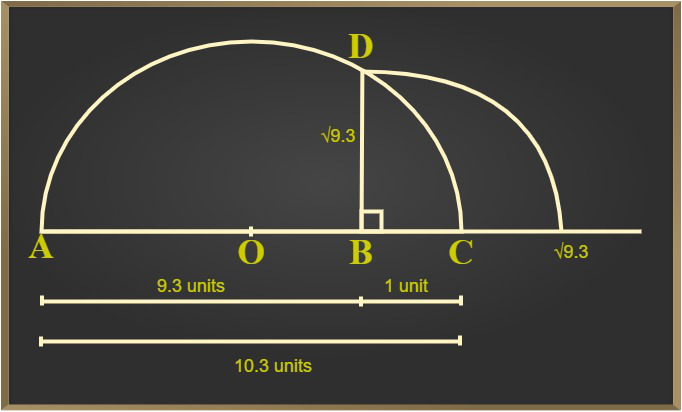
Pregunta 4: Representa (√9.3) en la recta numérica.
Solución:
Para representar √9.3 en la recta numérica, sigue los siguientes pasos,
Paso 1: Dibuje un segmento de línea de 9.3 unidades de largo, nombre la línea como AB.
Paso 2: Extender AB a C tal que BC=1 unidad.
Paso 3: Ahora, AC = 10,3 unidades. Sea el centro de AC O.
Paso 4: Dibuja un semicírculo con radio OC y centro O.
Paso 5: Dibuje un BD perpendicular a AC en el punto B que interseca el semicírculo en D.
Paso 6: Únase a BD.
Paso 7: Tomando BD como radio y B como punto central y dibuja un arco que toque el segmento de línea.
El punto donde se cruza con el segmento de línea está a una distancia de √9.3 de B como se muestra en la figura.
Pregunta 5: Racionalizar los denominadores de lo siguiente:
(yo) 1/√7
(ii) 1/(√7-√6)
(iii) 1/(√5+√2)
(iv) 1/(√7-2)
Solución:
(yo) 1/√7
Multiplicando y dividiendo 1/√7 por √7 obtenemos,
(1×√7)/(√7×√7) = √7/7
= √7/7
(ii) 1/(√7-√6)
Multiplica y divide 1/(√7-√6) por (√7+√6) obtenemos,
[1/(√7-√6)]×(√7+√6)/(√7+√6) = (√7+√6)/(√7-√6)(√7+√6)
= (√7+√6)/√7 2 -√6 2 [Como, (a+b)(ab) = a 2 -b 2 ]
= (√7+√6)/(7-6)
= (√7+√6)/1
= √7+√6
(iii) 1/(√5+√2)
Multiplica y divide 1/(√5+√2) por (√5-√2) obtenemos,
[1/(√5+√2)]×(√5-√2)/(√5-√2) = (√5-√2)/(√5+√2)(√5-√2)
= (√5-√2)/(√5 2 -√2 2 ) [Como, (a+b)(ab) = a 2 -b 2 ]
= (√5-√2)/(5-2)
= (√5-√2)/3
(iv) 1/(√7-2)
Multiplica y divide 1/(√7-2) por (√7+2) obtenemos,
1/(√7-2)×(√7+2)/(√7+2) = (√7+2)/(√7-2)(√7+2)
= (√7+2)/(√7 2 -2 2 ) [Como, (a+b)(ab) = a 2 -b 2 ]
= (√7+2)/(7-4)
= (√7+2)/3
Publicación traducida automáticamente
Artículo escrito por Mandeep_Sheoran y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA