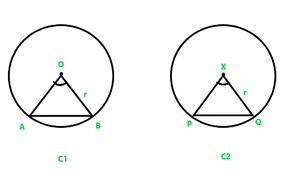
Pregunta 1. Recuerda que dos círculos son congruentes si tienen el mismo radio. Demostrar que cuerdas iguales de círculos congruentes subtienden ángulos iguales en sus centros.
Solución:
Dado:
Dos círculos congruentes C1 y C2
AB es el acorde de C1
y PQ es el acorde de C2
AB = PQ
Para probar: el ángulo subtendido por las cuerdas AB y PQ son iguales, es decir, ∠AOB = ∠PXQ
Prueba:
En △AOB y △PXQ
AO = PX (los radios de los círculos congruentes son iguales)
BO = QX (los radios de los círculos congruentes son iguales)
AB = PQ (Dado)
△AOB ⩭ △PXQ (regla de congruencia SSS)
Por lo tanto, ∠AOB = ∠PXQ (CPCT)
Pregunta 2. Demuestra que si las cuerdas de círculos congruentes subtienden ángulos iguales en sus centros, entonces las cuerdas son iguales.
Solución:
Dado:
Dos círculos congruentes C1 y C2
AB es el acorde de C1 y PQ es el acorde de C2
& ∠AOB = ∠PXQ
Probar :
En △AOB y △PXQ,
AO = PX (los radios de los círculos congruentes son iguales)
∠AOB = ∠PXQ (Dado)
BO = QX (los radios de los círculos congruentes son iguales)
△AOB ⩭ △PXQ (regla de congruencia SAS)
Por lo tanto, AB = PQ (CPCT)
Publicación traducida automáticamente
Artículo escrito por vermaman947 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA