Pregunta 1. Dibuja diferentes pares de círculos. ¿Cuántos puntos tiene cada par en común? ¿Cuál es el número máximo de puntos comunes?
Solución :
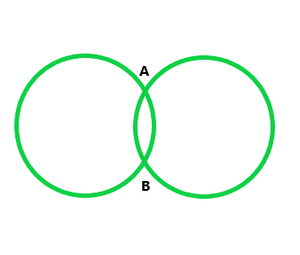
(i) Dos puntos comunes
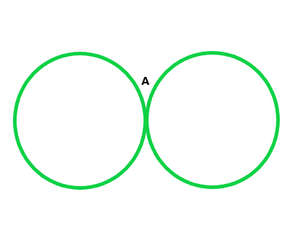
(ii) Un punto común
(iii) Un punto común
(iv) Ningún punto común
(v) Ningún punto común
Como podemos analizar desde arriba, dos círculos pueden cortarse como máximo en dos puntos.
Pregunta 2. Supón que te dan un círculo. Dar una construcción para encontrar su centro.
Solución:
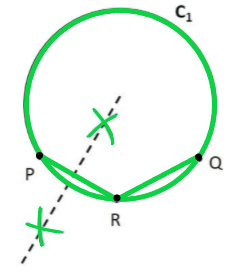
Sea el círculo C1
Necesitamos encontrar su centro.
Paso 1: Toma los puntos P, Q, R en el círculo
Paso 2: Únete a PR y RQ.
Sabemos que la mediatriz de una cuerda pasa por el centro
Entonces, construimos bisectrices perpendiculares de PR y RQ
Paso 3: Toma una brújula. Con el punto P como extremo puntiagudo y R como el extremo del lápiz de la brújula, marque un arco por encima y por debajo de PR. Haz lo mismo con R como extremo puntiagudo P como extremo de lápiz de la brújula.
Paso 4: Une los puntos intersecados por los arcos.
La línea formada es la mediatriz de PR.
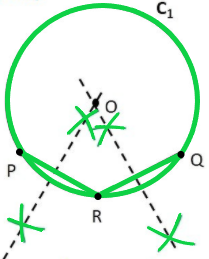
Paso 5: Tome la brújula, con el punto R como extremo puntiagudo y Q como el extremo del lápiz de la brújula, marque un arco por encima y por debajo de RQ.
Haz lo mismo con Q como extremo puntiagudo y R como extremo de lápiz de la brújula.
Paso 6: Une los puntos intersecados por los arcos.
La línea formada es la mediatriz de RQ.
Paso 7: El punto donde se cruzan dos bisectrices perpendiculares es el centro del círculo. Márcalo como el punto O.
Por lo tanto, O es el centro del círculo dado.
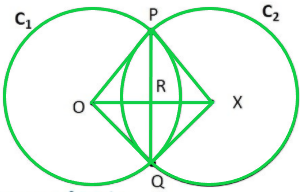
Pregunta 3: Si dos círculos se cortan en dos puntos, demuestre que sus centros se encuentran en la bisectriz perpendicular de la cuerda común.
Solución:
Dado,
Sea el círculo C1 de centro O y el círculo C2 de centro X, PQ es la cuerda común.
Para probar: OX es la bisectriz perpendicular de PQ, es decir
1. PR = RQ
2. ∠PRO = ∠PRX = ∠QRO = ∠QRX = 90°
Construcción:
Únase a PO, PX, QO, QX
Prueba:
En △POX y △QOX
OP = OQ (Radio del círculo C1)
XP = XQ (Radio del círculo C2)
BUEY = BUEY (Común)
∴ △POX ≅ △QOX (regla de congruencia SSS)
∠POX = ∠QOX (CPCT) —-(1)
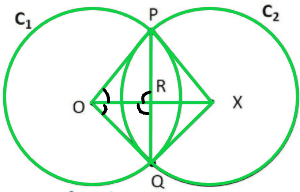
También,
En △POR y △QOR
OP = OQ (Radio del círculo C1)
∠POR = ∠QOR (De (1))
O = O (Común)
∴ △OPX ≅ △OQX (regla de congruencia SAS)
PR = QR (CPCT)
& ∠PRO = ∠QRO (CPCT) —-(2)
Como PQ es una recta
∠PRO + ∠QRO = 180° (par lineal)
∠PRO + ∠PRO= 180° (De (2))
2∠PRO = 180°
∠PRO = 180° / 2
∠PRO = 90°
Por lo tanto,
∠QRO = ∠PRO = 90°
También,
∠PRX = ∠QRO = 90° (Ángulos verticalmente opuestos)
∠QRX = ∠PRO = 90° (Ángulos verticalmente opuestos)
Ya que, ∠PRO = ∠PRX = ∠QRO = ∠QRX = 90°
∴ OX es la mediatriz de PQ
Publicación traducida automáticamente
Artículo escrito por vermaman947 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA