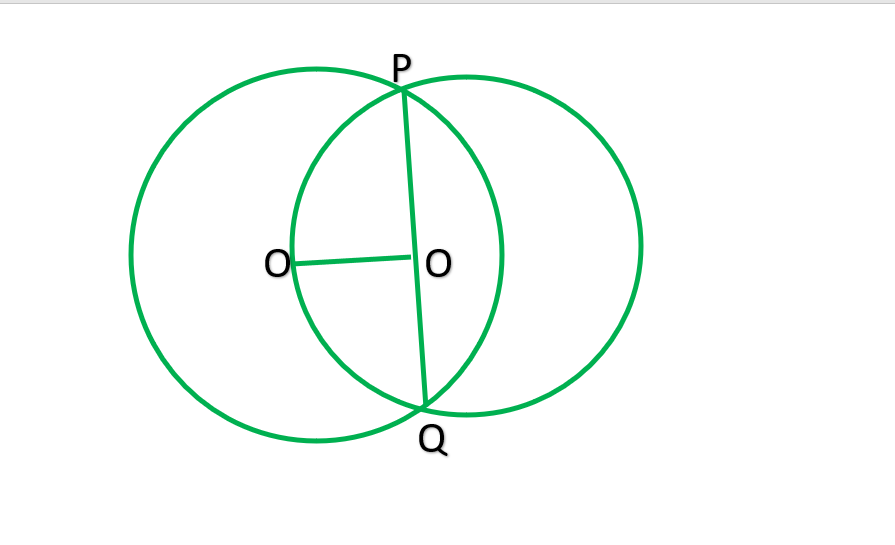
Pregunta 1. Dos círculos de 5 cm y 3 cm de radio se cortan en dos puntos y la distancia entre sus centros es de 4 cm. Encuentra la longitud de la cuerda común.
Solución:
Dado: OP=4cm, AP=3cm, QR=5cm
Para encontrar: En ∆APO:
AO²=5²=25
OP²=4²=16
AP²=3²=9
OP²+AP²=AO²
POR recíproco del teorema de Pitágoras
ΔAPO: es un derecho ∠D=P
Ahora, en el círculo más grande OP es perpendicular AB
AP=½AB —————-(perpendicular desde el centro del círculo a una cuerda biseca la cuerda)
3=½AB
6=AB
∴ Por lo tanto, la longitud de la cuerda común es de 6 cm.
Pregunta 2. Si dos cuerdas iguales de un círculo se cortan dentro del círculo, demuestre que la línea que une el punto de intersección con el centro forma ángulos iguales con las cuerdas.
Solución:
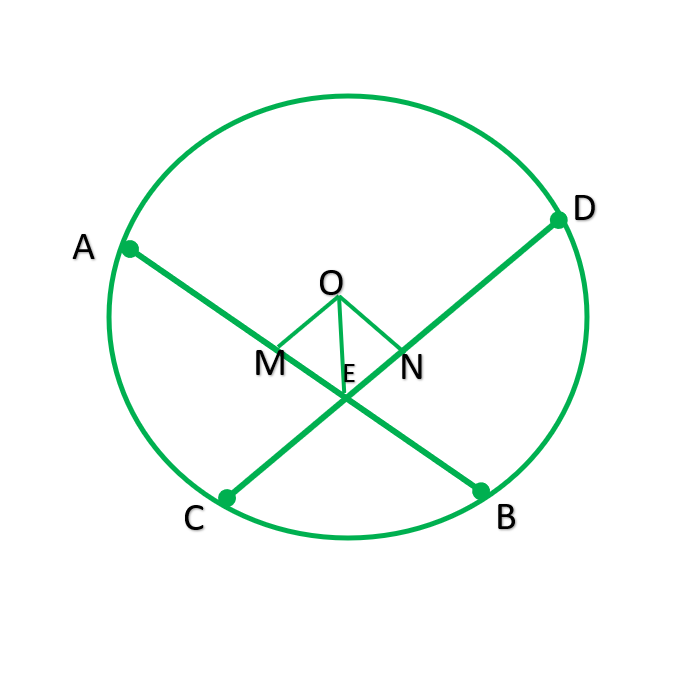
Dado: Cuerda igual AB y CD se cortan en P.
Para encontrar: AP=PD y PB=PC
Construcción: Dibuje OM perpendicular AB ,ON perpendicular CD y únase a OP.
Como la perpendicular desde el centro biseca la cuerda
∴ AM=MB=½AB también CN=ND=½CD
AM=MB=CN=ND ——————1
Ahora, en ∆OMP y ∆ONP
ÁNGULO M=ÁNGULO N [90° ambos]
OP=OP [COMÚN]
ON=OM [las cuerdas iguales son equiláteras desde el centro]
∴ ∆OMP≅∆ONP
Por lo tanto MP=PN (CPCT) ——————2
i) de 1 y 2
AM+MP=ND+AN
AP=DP
ii)MB-MP=CN=PN
PB=PC
Pregunta 3. Si dos cuerdas iguales de un círculo se cortan dentro del círculo, probar que la línea que une el punto de intersección con el centro forma ángulos iguales con las cuerdas.
Solución:
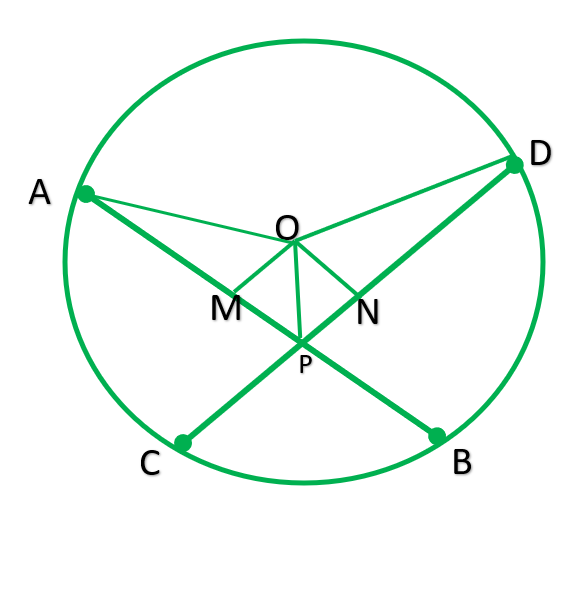
Dado: Cuerdas iguales AB y CD se cortan en P.
Para probar: ángulo1=ángulo=2
Construcción: Dibuje OM perpendicular AB & ON perpendicular CD.
Solución: En ∆OMP y ∆ONP
Ángulo M= Ángel N [90° cada uno]
OP=OP [común]
OM=ON —————[ Las cuerdas iguales están a la misma distancia del centro]
∴ ∆OMP≅∆ONP ———-[lado derecho]
∴ ∠1=∠2 ———–[CPCT]
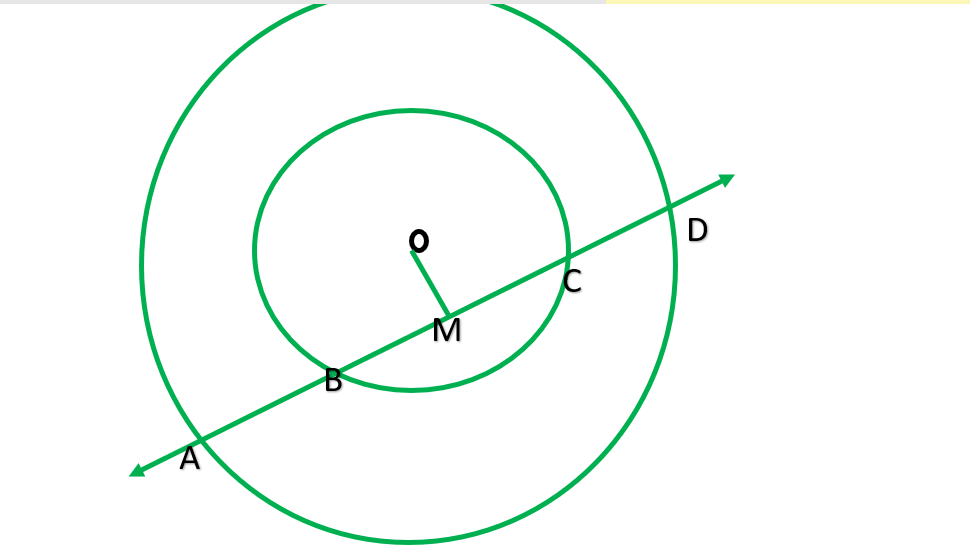
Pregunta 4. Si una línea corta dos círculos concéntricos (círculos con el mismo centro) con centro O en A, B, C y D, prueba que AB = CD (ver Figura).
Solución:
Dado: dos círculos concéntricos con O. Una línea los interseca en A, B, C y D
Para probar: AB=CD
construcción: Dibuje OM ⊥ AD, en un círculo más grande AD es el acorde OM ⊥ AD.
∴AM=MD —————-[⊥ desde el centro del círculo de un círculo biseca la cuerda] __________ 1
El círculo más pequeño:
BC es el acorde OM ⊥ BC
BM=MC ——————-[⊥ desde el centro del círculo de un círculo biseca la cuerda] __________ 2
restando 1-2
AM-BM=MD-MC
AB=CD
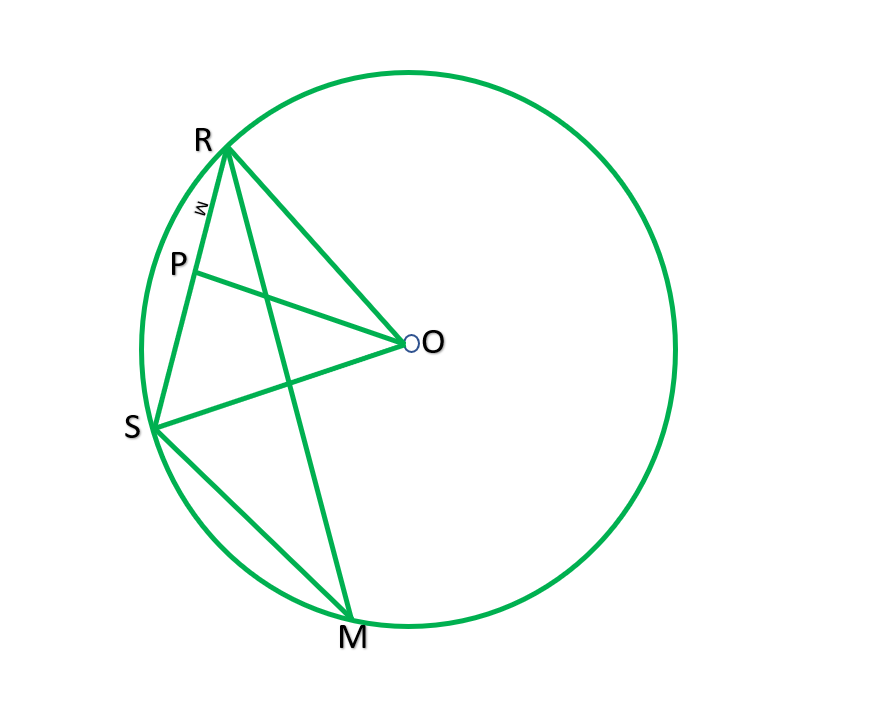
Pregunta 5. Tres niñas Reshma, Salma y Mandip están jugando parándose en un círculo de 5m de radio dibujado en un parque. Reshma le lanza una pelota a Salma, Salma a Mandip, Mandip a Reshma. Si la distancia entre Reshma y Salma y entre Salma y Mandip es de 6 m cada una, ¿cuál es la distancia entre Reshma y Mandip?
Solución:
Para encontrar RM=?
Que Reshma, Salma y Mandip sean R,S,M
Construcción: Dibujar OP ⊥ RS unir OR y OS.
RP=½RS ___________[⊥ desde el centro biseca la cuerda]
PR=½*6=3m
En ΔORP derecho
OP²=OR²-PR²
OP= √ 5² -3²
=√259 =√16 =4
Área de ΔORS=½*RS*OP
=½*6*4=12m² —————–1
Ahora, ∠N=90°
Área de ΔORS=½*SO*RN
=½*SO*RN ——————-2
Arriba, 1=2
12=½*5*RN
12/5*2=RN
RN=4.8
RM=2*RN _________________[⊥ desde el centro biseca la cuerda]
=2*4.8
9,6 m
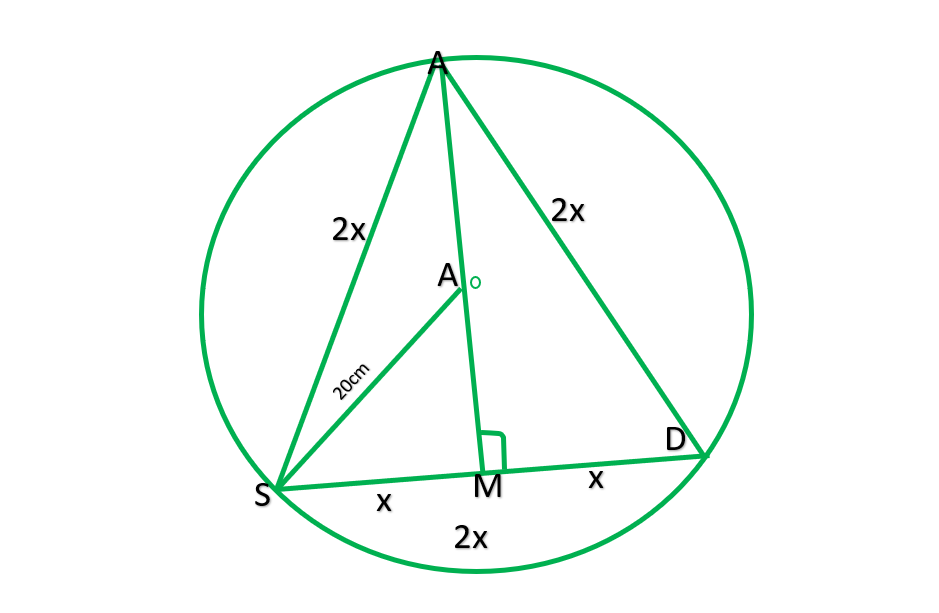
Pregunta 6. Un parque circular de 20m de radio está situado en una colonia. Tres niños, Ankur, Syed y David, están sentados a la misma distancia en su límite. Cada niño tiene un teléfono de juguete en la mano para hablar entre ellos. Encuentra la longitud de la cuerda de cada teléfono.
Solución:
Dibuja AM⊥SD
AS=SD=AD
∴ ASD es el equilátero Δ
Sea cada lado de Δ-2xm
SM=2x/2=x
Ahora en Δ DMS, por el teorema de Pitágoras
AM²+SM²=AS²
AM²= AS²- SM²
AM=√(2x²+x² )
==√(3x² )
AM =√3x
OM=AM-AO
OM=√3x-20
Ahora en la derecha ΔOMS
OM²+SM²=SO²
(√3x-20)²+2x²+x²=20²
20²+400-40√3x+x^2=400
4x²=40√3x
4xx=40√3x
X=(40√3)/4
X=10√3x
Longitud de cada string = 2x
=2*10√3xm
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA