Dado un número N , la tarea es encontrar la suma de los cubos de signos alternos de los primeros N números naturales, es decir,
1 3 – 2 3 + 3 3 – 4 3 + 5 3 – 6 3 + ….
Ejemplos:
Entrada: N = 2
Salida: -7
Explicación:
Suma requerida = 1 3 – 2 3 = -7
Entrada: N = 3
Salida: 20
Explicación:
Suma requerida = 1 3 – 2 3 + 3 3 = 20
Enfoque ingenuo: una solución simple es resolver este problema iterando sobre un bucle desde a N y calculando la suma alternando el signo cada vez.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to compute
// the sum of cubes with
// alternating sign
#include <iostream>
using namespace std;
// Function to compute sum
// of the cubes with
// alternating sign
int summation(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
return sum;
}
// Driver code
int main()
{
int n = 3;
cout << summation(n);
return 0;
}
Java
// Java implementation to compute
// the sum of cubes with
// alternating sign
import java.util.*;
class GFG {
// Function to compute sum
// of the cubes with
// alternating sign
static int summation(int n)
{
int sum = 0;
for(int i = 1; i <= n; i++)
{
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
}
return sum;
}
// Driver code
public static void main(String[] args)
{
int n = 3;
System.out.println(summation(n));
}
}
// This code is contributed by offbeat
Python3
# Python3 implementation to # compute the sum of cubes # with alternating sign # Function to compute sum # of the cubes with # alternating sign def summation(n): sum = 0 for i in range(1, n + 1): if i % 2 == 1: sum = sum + (i * i * i) else: sum = sum - (i * i * i) return sum # Driver code n = 3 print(summation(n)) # This code is contributed by ishayadav181
C#
// C# implementation to compute
// the sum of cubes with
// alternating sign
using System;
class GFG{
// Function to compute sum
// of the cubes with
// alternating sign
static int summation(int n)
{
int sum = 0;
for(int i = 1; i <= n; i++)
{
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
}
return sum;
}
// Driver code
public static void Main(String[] args)
{
int n = 3;
Console.WriteLine(summation(n));
}
}
// This code is contributed by sapnasingh4991
Javascript
<script>
// JavaScript implementation to compute
// the sum of cubes with
// alternating sign
// Function to compute sum
// of the cubes with
// alternating sign
function summation(n)
{
let sum = 0;
for (let i = 1; i <= n; i++)
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
return sum;
}
// Driver code
let n = 3;
document.write(summation(n));
// This code is contributed by Surbhi Tyagi
</script>
20
Complejidad de tiempo: O(n)
Espacio Auxiliar: O(1)
Enfoque eficiente: la observación clave en el problema es que cada número par tiene un signo negativo, es decir, se usa para reducir la suma total. Por lo tanto, si calculamos la suma de cubos de números pares e impares individualmente, entonces la suma total se puede calcular fácilmente.
- Recuento de números pares o impares en los primeros N números naturales
=>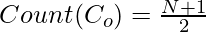
=>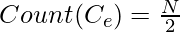
- Suma de los primeros términos pares
=>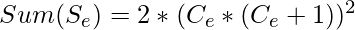
- Suma de los primeros términos impares
=>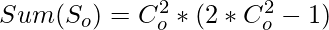
- Suma total
=>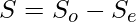
=>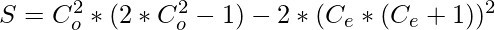
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to compute
// the sum of cubes with
// alternating sign
#include <bits/stdc++.h>
using namespace std;
// Function to compute sum
// of the cubes with alternating sign
int summation(int N)
{
int co = (N + 1) / 2;
int ce = (N) / 2;
int se = 2 * ((ce * (ce + 1))
* (ce * (ce + 1)));
int so = (co * co)
* (2 * ((co * co)) - 1);
return so - se;
}
// Driver Code
int main()
{
int n = 3;
cout << summation(n);
return 0;
}
Java
// Java implementation to compute
// the sum of cubes with
// alternating sign
import java.util.*;
class GFG{
// Function to compute sum
// of the cubes with
// alternating sign
static int summation(int N)
{
int co = (N + 1) / 2;
int ce = (N) / 2;
int se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)));
int so = (co * co) * (2 * ((co * co)) - 1);
return so - se;
}
// Driver code
public static void main(String[] args)
{
int n = 3;
System.out.println(summation(n));
}
}
// This code is contributed by offbeat
Python3
# Python3 implementation to compute # the sum of cubes with # alternating sign # Function to compute sum of # the cubes with alternating sign def summation(N): co = (N + 1) / 2 co = int(co) ce = N / 2 ce = int(ce) se = 2 * ((ce * (ce + 1)) * (ce * (ce + 1))) so = (co * co) * (2 * (co * co) - 1) return so - se # Driver Code n = 3 print(summation(n)) # This code is contributed by ishayadav181
C#
// C# implementation to compute
// the sum of cubes with
// alternating sign
using System;
class GFG{
// Function to compute sum
// of the cubes with
// alternating sign
static int summation(int N)
{
int co = (N + 1) / 2;
int ce = (N) / 2;
int se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)));
int so = (co * co) * (2 * ((co * co)) - 1);
return so - se;
}
// Driver code
public static void Main(String[] args)
{
int n = 3;
Console.WriteLine(summation(n));
}
}
// This code is contributed by Rohit_ranjan
Javascript
<script>
// javascript implementation to compute
// the sum of cubes with
// alternating sign
// Function to compute sum
// of the cubes with
// alternating sign
function summation(N)
{
var co = parseInt((N + 1) / 2);
var ce = parseInt((N) / 2);
var se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)));
var so = (co * co) * (2 * ((co * co)) - 1);
return so - se;
}
// Driver code
var n = 3;
document.write(summation(n));
// This code is contributed by Amit Katiyar
</script>
20
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)