Suma de los primeros N números de estrellas

Dado un número N , la tarea es encontrar la suma de los primeros N números de estrellas .
Los primeros números de estrellas son 1, 13, 37, 73, ..
Ejemplos:

Entrada: N = 2
Salida: 14
Explicación: 1, 13 son los primeros dos números de estrella.

Entrada: N = 3
Salida: 51

Enfoque 1:

^{El número} de estrella N se da como $6*n^2 - 6*n + 1$
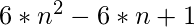
Ejecute un ciclo de 1 a N para encontrar los primeros N números de estrellas.
Agregue todos los números de estrellas calculados anteriormente.
Devolver la suma.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program to find the sum of
// the first N Star Number
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the N-th
// Star Number
int star_num(int n)
{
     
    // Formula to calculate nth
    // Star Number
    return (6 * n * n - 6 * n + 1);
}
 
// Function to find the sum of the
// first N Star Number
int sum_star_num(int n)
{
     
    // Variable to store the sum
    int summ = 0;
     
    // Iterating from 1 to N
    for(int i = 1; i < n + 1; i++)
    {
         
        // Finding the sum
        summ += star_num(i);
    }
    return summ;
}
 
// Driver code
int main()
{
    int n = 3;
     
    cout << sum_star_num(n);
}
 
// This code is contributed by spp____

Java

// Java program to find the sum of
// the first N Star Number
class GFG{
 
// Function to find the N-th
// Star Number
static int star_num(int n)
{
     
    // Formula to calculate nth
    // Star Number
    return (6 * n * n - 6 * n + 1);
}
 
// Function to find the sum of the
// first N Star Number
static int sum_star_num(int n)
{
     
    // Variable to store the sum
    int summ = 0;
     
    // Iterating from 1 to N
    for(int i = 1; i < n + 1; i++)
    {
         
        // Finding the sum
        summ += star_num(i);
    }
    return summ;
}
 
// Driver code
public static void main(String[] args)
{
    int n = 3;
     
    System.out.println(sum_star_num(n));
}
}
 
// This code is contributed by rock_cool

Python3

# Python3 program to find the
# sum of the first N 
# star numbers
 
# Function to find the
# N-th star
# number
def star_num(n):
  
    # Formula to calculate 
    # nth star
    # number
    return (6 * n * n - 6 * n + 1)
    
# Function to find the sum of
# the first N star numbers
def sum_star_num(n) :
     
    # Variable to store
    # the sum
    summ = 0
     
    # Iterating in the range
    # 1 to N
    for i in range(1, n + 1):
        summ += star_num(i)
     
    return summ
   
# Driver code
n = 3
print(sum_star_num(n))

C#

// C# program to find the sum of
// the first N Star Number
using System;
class GFG{
 
// Function to find the N-th
// Star Number
static int star_num(int n)
{
     
    // Formula to calculate nth
    // Star Number
    return (6 * n * n - 6 * n + 1);
}
 
// Function to find the sum of the
// first N Star Number
static int sum_star_num(int n)
{
     
    // Variable to store the sum
    int summ = 0;
     
    // Iterating from 1 to N
    for(int i = 1; i < n + 1; i++)
    {
         
        // Finding the sum
        summ += star_num(i);
    }
    return summ;
}
 
// Driver code
public static void Main(String[] args)
{
    int n = 3;
     
    Console.WriteLine(sum_star_num(n));
}
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
 
    // Javascript program to find the sum of    
    // the first N Star Number
     
    // Function to find the N-th
    // Star Number
    function star_num(n)
    {
 
        // Formula to calculate nth
        // Star Number
        return (6 * n * n - 6 * n + 1);
    }
 
    // Function to find the sum of the
    // first N Star Number
    function sum_star_num(n)
    {
 
        // Variable to store the sum
        let summ = 0;
 
        // Iterating from 1 to N
        for(let i = 1; i < n + 1; i++)
        {
 
            // Finding the sum
            summ += star_num(i);
        }
        return summ;
    }
     
    let n = 3;
       
    document.write(sum_star_num(n));
     
</script>

Producción

Complejidad temporal: O(N).
Espacio Auxiliar: O(1)

Enfoque eficiente:

Ya sabemos 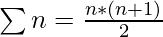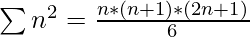$\sum n = \frac{n*(n+1)}{2}$ , $\sum n^2 = \frac{n*(n+1)*(2n+1)}{6}$ y $\sum n^3 = \frac{n*(n+1)}{2}^2$ $\sum 1 = n$
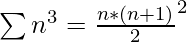
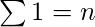
N ^número de estrella se da como $6*n^2 - 6*n + 1$
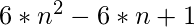
Entonces, la suma de los primeros N números de estrellas es $\sum 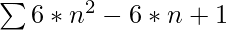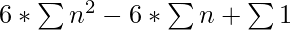6*n^2 - 6*n + 1$
Suma =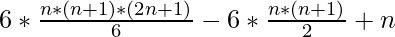 $6*\sum n^2 - 6*\sum n + \sum 1$
Suma =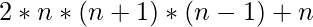 $6*\frac{n*(n+1)*(2n+1)}{6} - 6*\frac{n*(n+1)}{2} + n$
Suma = $2*n*(n+1)*(n-1) + n$
Calcula la suma y la devolución.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program to find the
// sum of the first N
// star numbers
#include <bits/stdc++.h>
 
using namespace std;
 
// Function to find the
// sum of the first N
// star number
int sum_star_num(int n)
{
     
    // Variable to store
    // the sum
    int summ = 2 * n * (n + 1) * (n - 1) + n;
     
    return summ;
}
 
// Driver code
int main()
{
    int n = 3;
     
    cout << sum_star_num(n);
    return 0;
}
 
// This code is contributed by Amit Katiyar

Java

// Java program to find the
// sum of the first N 
// star numbers
class GFG{
     
    // Function to find the
    // sum of the first N
    // star number
    static int sum_star_num(int n)
    {
 
        // Variable to store
        // the sum
        int summ = 2 * n * (n + 1) * (n - 1) + n;
 
        return summ;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 3;
        System.out.println(sum_star_num(n));
    }
}
 
// This code is contributed by PrinciRaj1992

Python3

# Python3 program to find the
# sum of the first N 
# star numbers
 
# Function to find the
# sum of the first N
# star number
def sum_star_num(n) :
     
    # Variable to store
    # the sum
    summ = 2 * n*(n + 1)*(n-1) + n
     
    return summ
   
# Driver code
n = 3
print(sum_star_num(n))

C#

// C# program to find the
// sum of the first N
// star numbers
using System;
 
class GFG{
     
// Function to find the
// sum of the first N
// star number
static int sum_star_num(int n)
{
 
    // Variable to store
    // the sum
    int summ = 2 * n * (n + 1) * (n - 1) + n;
 
    return summ;
}
 
// Driver code
public static void Main(String[] args)
{
    int n = 3;
     
    Console.WriteLine(sum_star_num(n));
}
}
 
// This code is contributed by PrinciRaj1992

Javascript

<script>
// Javascript program to find the
// sum of the first N
// star numbers
 
// Function to find the
// sum of the first N
// star number
function sum_star_num(n)
{
     
    // Variable to store
    // the sum
    let summ = 2 * n * (n + 1) * (n - 1) + n;
     
    return summ;
}
 
// Driver code
let n = 3;
 
document.write(sum_star_num(n));
 
// This code is contributed by rishavmahato348.
</script>

Producción

Complejidad temporal: O(1).
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por shubham prakash 1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta