Suma de los n primeros términos de una serie dada 3, 6, 11, …..

Dada una serie y un número n, la tarea es encontrar la suma de sus primeros n términos. A continuación se muestra la serie:
 

3, 6, 11, 20, ….

Ejemplos: 
 

Input: N = 2
Output: 9
The sum of first 2 terms of Series is
3 + 6 = 9

Input: N = 3
Output: 20
The sum of first 3 terms of Series is
3 + 6 + 11 = 20

Enfoque: Este problema se puede resolver fácilmente observando que el término n de la serie:
 

Sn = 3 + 6 + 11 + 20 … + hasta el enésimo término 
Sn = (1 + 2^1) + (2 + 2^2) + (3 + 2^3)+ (4 + 2^4) …… + hasta el enésimo término 
Sn = (1 + 2 + 3 + 4 …. + hasta el enésimo término) + ( 2^1 + 2^2 + 2^3 …… + hasta el enésimo término )

Observamos que Sn es una suma de dos series: AP y GP 
Como sabemos, la suma de los primeros n términos de AP viene dada por 

Y también la Suma de los primeros n términos de GP está dada por 

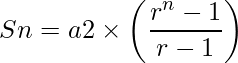
Por lo tanto, la suma total viene dada por la suma de AP y GP. 

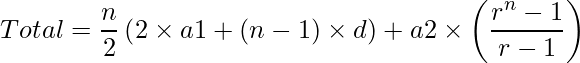
A continuación se muestra la implementación del enfoque anterior. 
 

// C++ program to find sum of first n terms
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate the sum
int calculateSum(int n)
{
    // starting number
    int a1 = 1, a2 = 2;
 
    // Common Ratio
    int r = 2;
 
    // Common difference
    int d = 1;
 
    return (n) * (2 * a1 + (n - 1) * d) / 2 + a2
               * (pow(r, n) - 1) / (r - 1);
}
 
// Driver code
int main()
{
 
    // N th term to be find
    int n = 5;
 
    // find the Sn
    cout << "Sum = " << calculateSum(n);
 
    return 0;
}

// Java program to find sum of first n terms
 
import java.io.*;
 
class GFG {
 
// Function to calculate the sum
static int calculateSum(int n)
{
    // starting number
    int a1 = 1, a2 = 2;
 
    // Common Ratio
    int r = 2;
 
    // Common difference
    int d = 1;
 
    return (n) * (2 * a1 + (n - 1) * d) / 2 + a2
            * (int)(Math.pow(r, n) - 1) / (r - 1);
}
 
// Driver code
    public static void main (String[] args) {
        // N th term to be find
    int n = 5;
 
    // find the Sn
    System.out.print( "Sum = " + calculateSum(n));
    }
}
// This code is contributed by inder_verma.

# Python3 program to find
# sum of first n terms
def calculateSum(n):
    # First term of AP
    a1 = 1;
     
    # First term of GP
    a2 = 2;
     
    # common ratio of GP
    r = 2;
     
    # common difference Of AP
    d = 1;
    return ((n) * (2 * a1 + (n - 1) * d) /
                   2 + a2 * (pow(r, n) - 1) /
                  (r - 1));
 
# Driver Code
 
# no. of the terms
# for the sum
n = 5;
 
# Find the Sn
print ("Sum =", int(calculateSum(n)))
 
# This code is contributed
# by Surendra_Gangwar

// C# program to find sum
// of first n terms
using System;
 
class GFG
{
 
// Function to calculate the sum
static int calculateSum(int n)
{
    // starting number
    int a1 = 1, a2 = 2;
 
    // Common Ratio
    int r = 2;
 
    // Common difference
    int d = 1;
 
    return (n) * (2 * a1 + (n - 1) * d) / 2 + a2 *
             (int)(Math.Pow(r, n) - 1) / (r - 1);
}
 
// Driver code
public static void Main ()
{
    // N th term to be find
    int n = 5;
     
    // find the Sn
    Console.WriteLine("Sum = " + calculateSum(n));
}
}
 
// This code is contributed
// by inder_verma

<?php
// PHP program to find sum of first n terms
 
// Function to calculate the sum
function calculateSum($n)
{
    // starting number
    $a1 = 1;
    $a2 = 2;
     
    // Common Ratio
    $r = 2;
     
    // Common difference
    $d = 1;
     
    return ($n) * (2 * $a1 + ($n - 1) * $d) / 2 +
            $a2 * (pow($r, $n) - 1) / ($r - 1);
}
 
// Driver code
 
// Nth term to be find
$n = 5;
 
// find the Sn
echo "Sum = ", calculateSum($n);
 
// This code is contributed
// by Shashank_Sharma
?>

<script>
 
// Javascript program to find sum of first n terms
// Function to calculate the sum
 
function calculateSum(n)
{
    // starting number
    let a1 = 1, a2 = 2;
 
    // Common Ratio
    let r = 2;
 
    // Common difference
    let d = 1;
 
    return (n) * (2 * a1 + (n - 1) * d) / 2 + a2
            * (Math.pow(r, n) - 1) / (r - 1);
}
 
// Driver code
 
    // N th term to be find
    let n = 5;
 
    // find the Sn
    document.write("Sum = " + calculateSum(n));
 
 
 
// This code is contributed by Mayank Tyagi
 
</script>

Sum = 77

Complejidad de tiempo: O (logn) 

Espacio Auxiliar: O(1)