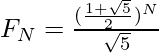Suma de números de Fibonacci | conjunto 2

Dado un número positivo N , la tarea es encontrar la suma de los primeros (N + 1) Números de Fibonacci .

Ejemplos:

Entrada: N = 3
Salida: 4
Explicación:
Los primeros 4 términos de la serie de Fibonacci son {0, 1, 1, 2}. Por lo tanto, la suma requerida = 0 + 1 + 1 + 2 = 4.

Entrada: N = 4
Salida: 7

Enfoque ingenuo: para conocer el enfoque más simple para resolver el problema, consulte la publicación anterior de este artículo.
Complejidad temporal: O(N)
Espacio auxiliar: O(1)

Enfoque eficiente: El enfoque anterior se puede optimizar mediante las siguientes observaciones y cálculos:

Sea S(N) la suma de los primeros N términos de la serie de Fibonacci. Ahora, para simplemente encontrar S(N) , calcule el (N + 2) ^-ésimo número de Fibonacci y reste 1 del resultado. El ^término N de esta serie se puede calcular mediante la fórmula:

$F_N = \frac{(\frac{1 + \sqrt{5}}{2})^{N}}{\sqrt{5}}$

Ahora el valor de S(N) se puede calcular mediante (F _{N + 2} – 1) .

Por lo tanto, la idea es calcular el valor de S _N utilizando la fórmula anterior:

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the sum of
// first N + 1 fibonacci numbers
void sumFib(int N)
{
   
    // Apply the formula
    long num = (long)round(pow((sqrt(5) + 1)
                               / 2.0, N + 2)
                           / sqrt(5));
 
    // Print the result
    cout << (num - 1);
}
 
// Driver Code
int main()
{
    int N = 3;
    sumFib(N);
    return 0;
}
 
// This code is contributed by Dharanendra L V.

Java

// Java program for the above approach
import java.io.*;
 
class GFG {
 
    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        long num = (long)Math.round(
            Math.pow((Math.sqrt(5) + 1)
                         / 2.0,
                     N + 2)
            / Math.sqrt(5));
 
        // Print the result
        System.out.println(num - 1);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int N = 3;
        sumFib(N);
    }
}

Python3

# Python program for the above approach
import math
 
# Function to find the sum of
# first N + 1 fibonacci numbers
def sumFib(N):
   
    # Apply the formula
    num = round(pow((pow(5,1/2) + 1) \
                    / 2.0, N + 2) \
                / pow(5,1/2));
 
    # Print the result
    print(num - 1);
 
# Driver Code
if __name__ == '__main__':
    N = 3;
    sumFib(N);
 
# This code is contributed by 29AjayKumar

C#

// C# program for the above approach
using System;
class GFG
{
 
    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        long num = (long)Math.Round(
            Math.Pow((Math.Sqrt(5) + 1)
                         / 2.0,
                     N + 2)
            / Math.Sqrt(5));
 
        // Print the result
        Console.WriteLine(num - 1);
    }
 
// Driver Code
static public void Main()
{
        int N = 3;
        sumFib(N);
}
}
 
// This code is contributed by jana_sayantan.

Javascript

<script>
 
// Javascript program for the above approach
 
    // Function to find the sum of
    // first N + 1 fibonacci numbers
    function sumFib(N)
    {
        // Apply the formula
        var num =  Math.round(Math.pow((Math.sqrt(5) + 1)
        / 2.0, N + 2) / Math.sqrt(5));
 
        // Print the result
        document.write(num - 1);
    }
 
    // Driver Code
     
        var N = 3;
        sumFib(N);
 
// This code contributed by umadevi9616
 
</script>

Producción:

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)

Enfoque alternativo: siga los pasos a continuación para resolver el problema:

El número N ^{de Fibonacci} también se puede calcular usando la función generadora .
La función generadora del número N de ^Fibonacci viene dada por:

$G(X) = \frac{X}{(1 - X - X^{2})}$

Por tanto, la función generadora de la suma de los números de Fibonacci viene dada por:

$G'(X) = \frac{X}{((1 - X - X^{2}) * (1 - X))}$

Después de la descomposición en fracciones parciales de G'(X) , el valor de G'(X) viene dado por:

$G'(X) = \frac{a}{(a + 1) * (a - b) * (X + a)} + \frac{b}{(b + 1) * (b - a) * ( X + b)} + \frac{1}{(a + 1) * (b + 1) * (X - 1)}$

dónde,
$a = \frac{(1 + \sqrt5)}{2}, b = \frac{(1 - \sqrt5)}{2}$

Por lo tanto, la fórmula para la suma de los números de Fibonacci viene dada por:

$S_{N} = \mid \frac{1}{b^{N + 1} + b^{N} + b^{N - 1} + b^{N - 2} } \mid - 1$

A continuación se muestra la implementación del enfoque anterior:

C++

// C++  program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the sum of
// first N + 1 fibonacci numbers
void sumFib(int N)
{
   
  // Apply the formula
  double num = (1 - sqrt(5)) / 2;
 
  long val = round(
    abs(1
        / (pow(num, N + 2)
           + pow(num, N + 1)
           + pow(num, N)
           + pow(num, N - 1)))
    - 1);
 
  // Print the result
  cout<<val;
}
 
// Driver Code
int main()
{
    int N = 3;
 
      // Function Call
    sumFib(N);
}
 
// This code is contributed by 29AjayKumar

Java

// Java program for the above approach
import java.io.*;
 
class GFG {
 
    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        double num = (1 - Math.sqrt(5)) / 2;
 
        long val = Math.round(
            Math.abs(1
                     / (Math.pow(num, N + 2)
                        + Math.pow(num, N + 1)
                        + Math.pow(num, N)
                        + Math.pow(num, N - 1)))
            - 1);
 
        // Print the result
        System.out.println(val);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int N = 3;
 
        // Function Call
        sumFib(N);
    }
}

Python3

# Python3 program for the above approach
import math
 
# Function to find the sum of
# first N + 1 fibonacci numbers
def sumFib(N):
     
    # Apply the formula
    num = (1 - math.sqrt(5)) / 2
 
    val = round(abs(1 / (pow(num, N + 2) +
                         pow(num, N + 1) +
                         pow(num, N) +
                         pow(num, N - 1))) - 1)
 
    # Print the result
    print(val)
 
# Driver Code
if __name__ == '__main__':
 
    N = 3
 
    # Function Call
    sumFib(N)
 
# This code is contributed by Surbhi Tyagi.

C#

// C# program for the above approach
 
 
using System;
 
public class GFG {
 
    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        double num = (1 - Math.Sqrt(5)) / 2;
 
        double val = Math.Round(
            Math.Abs(1
                     / (Math.Pow(num, N + 2)
                        + Math.Pow(num, N + 1)
                        + Math.Pow(num, N)
                        + Math.Pow(num, N - 1)))
            - 1);
 
        // Print the result
        Console.WriteLine(val);
    }
 
    // Driver Code
    public static void Main(String[] args)
    {
        int N = 3;
 
        // Function Call
        sumFib(N);
    }
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
 
// Javascript program for the above approach
 
    // Function to find the sum of
    // first N + 1 fibonacci numbers
    function sumFib(N) {
        // Apply the formula
        var num = ((1 - Math.sqrt(5)) / 2);
 
        var val = Math.round(
            Math.abs(1
                     / (Math.pow(num, N + 2)
                        + Math.pow(num, N + 1)
                        + Math.pow(num, N)
                        + Math.pow(num, N - 1)))
            - 1);
 
        // Print the result
        document.write(val);
    }
 
    // Driver Code
     
        var N = 3;
 
        // Function Call
        sumFib(N);
 
// This code is contributed by todaysgaurav
 
</script>

Producción:

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por debarpan_bose_chowdhury y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta