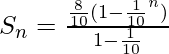Suma de series 8/10, 8/100, 8/1000, 8/10000. . . hasta N términos

Dado un entero positivo n , la tarea es encontrar la suma de la serie 

8/10 + 8/100 + 8/1000 + 8/10000. . . hasta el enésimo término

Ejemplos:

Entrada: n = 3
Salida: 0,888

Entrada: n = 5
Salida: 0,88888

Acercarse: 

La suma total hasta el término n de la serie GP dada se puede generalizar como-

La fórmula anterior se puede derivar siguiendo la serie de pasos:

La serie GP dada

 

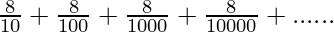
Aquí,

 

 

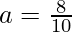
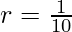
Por lo tanto, usando la fórmula de la suma de GP para r<1

Sustituyendo los valores de a y r en la ecuación anterior

Ilustración:

Entrada: n = 3
Salida: 0,888
Explicación:

S_{n}=\frac{8}{9}(1-(\frac{1}{10})^{3})
        = 0,888 * 0,999
        = 0,888

A continuación se muestra la implementación del problema anterior:

// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate sum of
// given series till Nth term
double sumOfSeries(double N)
{
    return (8 * ((pow(10, N) - 1) / pow(10, N))) / 9;
}
 
// Driver code
int main()
{
    double N = 5;
    cout << sumOfSeries(N);
    return 0;
}

// Java program to implement
// the above approach
import java.util.*;
public class GFG
{
   
    // Function to calculate sum of
    // given series till Nth term
    static double sumOfSeries(double N)
    {
        return (8
                * ((Math.pow(10, N) - 1) / Math.pow(10, N)))
            / 9;
    }
 
    // Driver code
    public static void main(String args[])
    {
        double N = 5;
        System.out.print(sumOfSeries(N));
    }
}
 
// This code is contributed by Samim Hossain Mondal.

# Python code for the above approach
 
# Function to calculate sum of
# given series till Nth term
def sumOfSeries(N):
    return (8 * (((10 ** N) - 1) / (10 ** N))) / 9;
 
# Driver code
N = 5;
print(sumOfSeries(N));
 
# This code is contributed by gfgking

// C# program to implement
// the above approach
using System;
class GFG
{
   
    // Function to calculate sum of
    // given series till Nth term
    static double sumOfSeries(double N)
    {
        return (8
                * ((Math.Pow(10, N) - 1) / Math.Pow(10, N)))
            / 9;
    }
 
    // Driver code
    public static void Main()
    {
        double N = 5;
        Console.WriteLine(sumOfSeries(N));
    }
}
 
// This code is contributed by ukasp.

<script>
        // JavaScript code for the above approach
 
        // Function to calculate sum of
        // given series till Nth term
        function sumOfSeries(N) {
            return (8 * ((Math.pow(10, N) - 1) / Math.pow(10, N))) / 9;
        }
 
        // Driver code
        let N = 5;
        document.write(sumOfSeries(N));
 
  // This code is contributed by Potta Lokesh
    </script>

0.88888

Tiempo Complejidad: O(1) 
Espacio Auxiliar: O(1)