Dado un número natural n , encuentre la suma de la serie suma del primer N número natural.
Serie-suma : es la suma de los primeros N números naturales, es decir, la serie-suma de 5 es 15 (1 + 2 + 3 + 4 + 5).
Número natural 1 2 3 4 5 6 Suma de números naturales (suma-serie) 1 3 6 10 15 21 Suma de series de suma 1 4 10 20 35 56
Ejemplo:
Entrada: N = 5
Salida: 35
Explicación:
La suma de la serie suma de {1, 2, 3, 4, 5} es decir, {1 + 3 + 6 + 10 + 15} es 35.Entrada: N = 2
Salida: 4
Explicación:
La suma de la serie suma de {1, 2}, es decir, {1 + 3} es 4.
Enfoque simple:
encuentre la serie de suma para cada valor de 1 a N y luego súmela.
- Cree una variable Total_sum para almacenar la serie de suma requerida.
- Iterar sobre el número de 1 a N
- Encuentre series de suma de cada valor usando las fórmulas sum = (N*(N + 1)) / 2
- Agregue el valor a Total_sum
- Al final, imprima el valor almacenado en Total_sum .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to implement
// the above approach
#include<bits/stdc++.h>
using namespace std;
// Function to find the sum
static long sumOfSumSeries(int N)
{
long sum = 0L;
// Calculate sum-series
// for every natural number
// and add them
for (int i = 1; i <= N; i++)
{
sum = sum + (i * (i + 1)) / 2;
}
return sum;
}
// Driver code
int main()
{
int N = 5;
cout << sumOfSumSeries(N);
}
// This code is contributed by Code_Mech
Java
// Java program to implement
// the above approach
class GFG {
// Function to find the sum
static long sumOfSumSeries(int N)
{
long sum = 0L;
// Calculate sum-series
// for every natural number
// and add them
for (int i = 1; i <= N; i++) {
sum = sum + (i * (i + 1)) / 2;
}
return sum;
}
// Driver code
public static void main(String[] args)
{
int N = 5;
System.out.println(sumOfSumSeries(N));
}
}
Python3
# Python3 program to implement # the above approach # Function to find the sum def sumOfSumSeries(N): _sum = 0 # Calculate sum-series # for every natural number # and add them for i in range(N + 1): _sum = _sum + (i * (i + 1)) // 2 return _sum # Driver code N = 5 print(sumOfSumSeries(N)) # This code is contributed by divyamohan123
C#
// C# program to implement
// the above approach
using System;
class GFG{
// Function to find the sum
static long sumOfSumSeries(int N)
{
long sum = 0L;
// Calculate sum-series
// for every natural number
// and add them
for(int i = 1; i <= N; i++)
{
sum = sum + (i * (i + 1)) / 2;
}
return sum;
}
// Driver code
public static void Main()
{
int N = 5;
Console.Write(sumOfSumSeries(N));
}
}
// This code is contributed by Nidhi_Biet
Javascript
<script>
// Javascript program to implement
// the above approach
// Function to find the sum
function sumOfSumSeries(N)
{
let sum = 0;
// Calculate sum-series
// for every natural number
// and add them
for (let i = 1; i <= N; i++)
{
sum = sum + (i * (i + 1)) / 2;
}
return sum;
}
let N = 5;
document.write(sumOfSumSeries(N));
// This code is contributed by suresh07.
</script>
35
Complejidad temporal : O (N)
Espacio auxiliar: O(1)
Enfoque eficiente:
Total_sum de la serie anterior se puede calcular directamente utilizando las siguientes fórmulas:
donde N es el número natural
Prueba de la fórmula anterior:
Supongamos que N = 5
- Luego, la suma es la suma de todos los elementos a continuación en la tabla, llamemos a esto » resultado «.
| 1 | ||||
| 1 | 2 | |||
| 1 | 2 | 3 | ||
| 1 | 2 | 3 | 4 | |
| 1 | 2 | 3 | 4 | 5 |
llenemos las celdas vacías con el mismo valor en otras columnas, llamemos a esto » totalSum «
| 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 3 | 4 | 5 |
Como la suma de N números se repite N veces
totalSum = N * [(N*(N + 1))/2]
datos poblados = (1 veces * 2) + (2 veces * 3) + (3 veces * 4) + (4 veces * 5)
= 1*2 + 2*3 + 3*4 ……… +(N-1)*N
=[(N-1) * (N) * (N+1)]/3
- Ya que,
resultado = suma total – datos poblados
= N * [(N*(N+1))/2] – [(N-1) * (N) * (N+1)]/3
= (N*(N+1) *(N+2))/6
- Por lo tanto
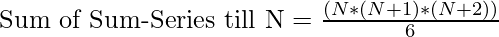
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to implement
// the above approach
#include <iostream>
#include <math.h>
using namespace std;
// Function to find the sum
long sumOfSumSeries(int n)
{
return (n * (n + 1) * (n + 2)) / 6;
}
// Driver code
int main ()
{
int N = 5;
cout << sumOfSumSeries(N);
return 0;
}
// This code is contributed
// by shivanisinghss2110
Java
// Java program to implement
// the above approach
class GFG {
// Function to find the sum
static long sumOfSumSeries(int n)
{
return (n * (n + 1) * (n + 2)) / 6;
}
// Driver code
public static void main(String[] args)
{
int N = 5;
System.out.println(sumOfSumSeries(N));
}
}
Python3
# Python3 program to implement # the above approach # Function to find the sum def sumOfSumSeries(n): return (n * (n + 1) * (n + 2)) // 6 # Driver code N = 5 print(sumOfSumSeries(N)) # This code is contributed by divyamohan123
C#
// C# program to implement the
// above approach
using System;
class GFG{
// Function to find the sum
static long sumOfSumSeries(int n)
{
return (n * (n + 1) * (n + 2)) / 6;
}
// Driver code
public static void Main(String[] args)
{
int N = 5;
Console.Write(sumOfSumSeries(N));
}
}
// This code is contributed by Ritik Bansal
Javascript
<script>
// Javascript program to implement
// the above approach
// Function to find the sum
function sumOfSumSeries(n)
{
return (n * (n + 1) * (n + 2)) / 6;
}
let N = 5;
document.write(sumOfSumSeries(N));
</script>
35
Complejidad del tiempo: O(1), teniendo en cuenta que la multiplicación, la suma y la división requieren un tiempo constante.
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por bhanuchand y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA