El Teorema de Pitágoras es un teorema bien conocido, que también es muy antiguo. El teorema de Pitágoras nos proporciona la relación entre los lados de un triángulo rectángulo. Un triángulo rectángulo consta de dos catetos y una hipotenusa. Los dos catetos se encuentran en un ángulo de 90° y la hipotenusa es el lado más largo del triángulo rectángulo y es el lado opuesto al ángulo recto.
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.
Fórmula para el teorema de Pitágoras
Considere el triángulo que se muestra a continuación, donde «a» es el lado perpendicular, «b» es la base y «c» es el lado de la hipotenusa, luego, de acuerdo con la definición, la fórmula del Teorema de Pitágoras se da como:

Prueba del teorema de Pitágoras
Veamos la forma tradicional de probar la fórmula del teorema de Pitágoras que dice que el área del cuadrado sobre la hipotenusa es igual a la suma de las áreas de los cuadrados sobre los dos lados más cortos. La siguiente figura muestra cuadrados dibujados en cada lado.

Considere tres cuadrados de lados a, b, c montados en los tres lados de un triángulo A, B y C respectivamente.
Por el teorema de Pitágoras:
Área del cuadrado A + Área del cuadrado B = Área del cuadrado C
que no es más que,
un 2 + segundo 2 = do 2
Ahora vamos a resolver algunos problemas para entender mejor el concepto.
Ejemplos de problemas sobre el teorema de Pitágoras
Problema 1: En el siguiente triángulo rectángulo, encuentre el valor de y.

Solución:
Por el enunciado del teorema de Pitágoras obtenemos,
=> z 2 = x 2 + y 2
Ahora, sustituyendo los valores directamente obtenemos,
=> 13 2 = 5 2 + y 2
=> 169 = 25 + y 2
=> y2 = 144
=> y = √144 = 12
Problema 2: dado un rectángulo de 4 cm de largo y 3 cm de ancho. ¿Encontrar la longitud de la diagonal del rectángulo?
Solución:

En el diagrama anterior, la longitud del rectángulo es de 4 cm y el ancho es de 3 cm.
Ahora tenemos que encontrar la distancia entre el punto A y el punto C o el punto B y el punto D. Ambos nos dan la misma respuesta porque los lados opuestos tienen la misma longitud, es decir, AC = BD
Ahora encontremos la distancia entre los puntos A y C dibujando una línea imaginaria.

Ahora el triángulo ACD es un triángulo rectángulo.
Entonces, por el enunciado del teorema de Pitágoras,
=> AC 2 = AD 2 + CD 2
=> CA 2 = 4 2 + 3 2
=> CA 2 = 25
=> CA = √25 = 5
Por lo tanto, la longitud de la diagonal del rectángulo dado es de 5 cm.
Recíproco del teorema de Pitágoras
El inverso del teorema de Pitágoras es muy similar al teorema de Pitágoras. Para entender este teorema debes pensar desde el reverso del teorema de Pitágoras.
Si el cuadrado de la longitud del lado más largo de un triángulo es igual a la suma de los cuadrados de los otros dos lados, entonces el triángulo es un triángulo rectángulo.
Fórmula y prueba del teorema de Pitágoras inverso
La fórmula será la misma ya que es simplemente inversa al teorema de Pitágoras. De acuerdo con el enunciado, necesitamos demostrar que se cumple la condición, entonces el triángulo debe ser un triángulo rectángulo, para eso debemos demostrar que el ángulo opuesto del lado más largo debe ser de 90 °.
Si hay un triángulo con longitud a, b y c

Suponemos que satisface c 2 = a 2 + b 2 y mirando el diagrama podemos decir que ∠C = 90° pero para demostrarlo necesitamos otro triángulo △EGF, como AC = EG = b y BC = FG = un.
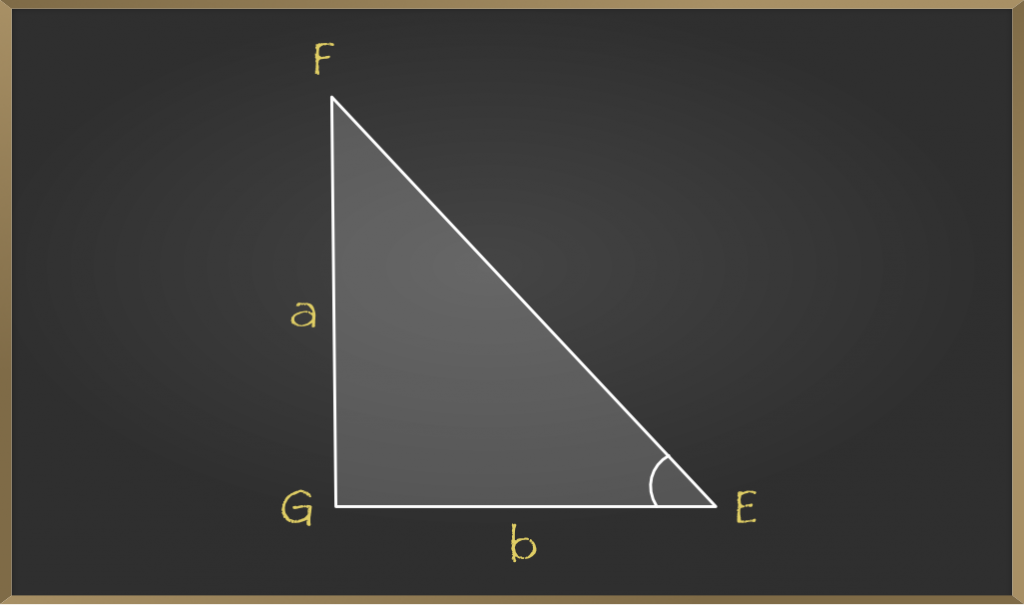
En △EGF, por el Teorema de Pitágoras:
=> EF 2 = EG 2 + FG2 2 = b 2 + a 2 …………(1)
En △ABC, por el Teorema de Pitágoras:
=> AB 2 = AC 2 + BC 2 = b 2 + a 2 …………(2)
De la ecuación (1) y (2), tenemos;
=> EF 2 = AB 2
=> EF = AB
=> △ ACB ≅ △EGF (Por postulado SSS)
=> ∠G es ángulo recto
Por lo tanto, △EGF es un triángulo rectángulo.
Por lo tanto, podemos decir que también se cumple el inverso del teorema de Pitágoras.
Ejemplos de problemas sobre el recíproco del teorema de Pitágoras
Problema 1: Los lados de un triángulo son 5, 12 y 13. Comprueba si el triángulo dado es un triángulo rectángulo o no.
Solución:
Dado,
=> un = 5
=> segundo = 12
=> c = 13
Usando el recíproco del Teorema de Pitágoras,
=> un 2 +b 2 = c 2
Sustituya los valores dados en la ecuación anterior,
=> 13 2 = 5 2 +12 2
=> 169 = 25 + 144
=> 169 = 169
Entonces, las longitudes dadas satisfacen la condición anterior.
Por lo tanto, el triángulo dado es un triángulo rectángulo.
Problema 2: El lado de un triángulo mide 9 cm, 11 cm y 6 cm. ¿Este triángulo es un triángulo rectángulo? Si es así, ¿de qué lado está la hipotenusa?
Solución:
Sabemos que la hipotenusa es el lado más largo. Si 9 cm, 11 cm y 6 cm son las longitudes del triángulo anguloso, entonces 11 cm será la hipotenusa.
Usando el recíproco del teorema de Pitágoras, obtenemos
=> (11) 2 = (9) 2 + (6) 2
=> 121 = 81 + 36
=> 121 ≠ 117
Dado que ambos lados no son iguales, 9 cm, 11 cm y 6 cm no son el lado del triángulo rectángulo.
Publicación traducida automáticamente
Artículo escrito por dadimadhav y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA