Teorema – Hay uno y solo un círculo que pasa por tres puntos no colineales dados | Clase 9 Matemáticas

Enunciado del teorema: Hay una y sólo una circunferencia que pasa por tres puntos no colineales dados.

Diagrama requerido:

Dado: Tres puntos no colineales P, Q y R.

Para probar: hay un y solo un círculo que pasa por P, Q y R.

Construcción: Unir PQ y QR. Dibujar bisectrices perpendiculares AL y BM de PQ y RQ respectivamente. Dado que P, Q, R no es colineal. Por tanto, las bisectrices perpendiculares AL y BM no son paralelas. Deje que AL y BM se intersequen en O. Únase a OP, OQ y OR.

Prueba

Dado que O se encuentra en la bisectriz perpendicular de PQ. Por lo tanto,

OP = OQ 

Nuevamente, O se encuentra en la bisectriz perpendicular de QR. Por lo tanto,  

OQ = O

Así, OP = OQ = OR = r (digamos).

Tomando O como centro trazar una circunferencia de radio s. Claramente, C (0, s) pasa por P, Q y R. Esto prueba que hay un círculo que pasa por los puntos P, Q y R. Ahora demostraremos que este es el único círculo que pasa por P. Q y R. Sea, si es posible, otra circunferencia de centro O’ y radio r, que pase por los puntos P, Q y R. Entonces, O’ estará sobre las mediatrices AL de PQ y BM de QR. Como dos rectas no pueden intersecarse en más de un punto, entonces O’ debe coincidir con O. Como OP = r, O’P = s y O y O’ coinciden, lo que significa que,

r = s

Por lo tanto,

C(O, r) ≅ (O’, s)

Por tanto, hay una y sólo una circunferencia que pasa por tres puntos no colineales P, Q y R.

Ejemplos

Ejemplo 1: Escriba los procedimientos de construcción paso a paso para encontrar el centro del círculo. 

Solución:

Sea el círculo C1. Necesitamos encontrar su centro .

Paso 1: Toma los puntos P, Q, R en el círculo 

Paso 2: Únete a PR y RQ.

Sabemos que la mediatriz de una cuerda pasa por el centro. Entonces, construimos bisectrices perpendiculares de PR y RQ.

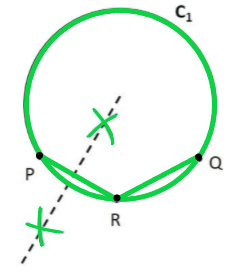
Paso 3: Toma una brújula. Con el punto P como el extremo puntiagudo y R como el extremo del lápiz de la brújula, marque un arco por encima y por debajo de PR. Haz lo mismo con R como extremo puntiagudo P como extremo de lápiz de la brújula.

Paso 4: Une los puntos intersecados por los arcos. La línea formada es la mediatriz de PR.

Paso 5: Tome una brújula, con el punto R como extremo puntiagudo y Q como el extremo del lápiz de la brújula, marque un arco por encima y por debajo de RQ. Haz lo mismo con Q como el extremo puntiagudo y R como el extremo del lápiz de la brújula.

Paso 6: Une los puntos intersecados por los arcos. La línea formada es la mediatriz de RQ.

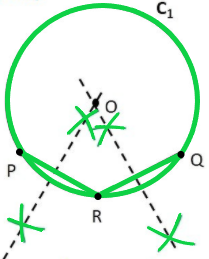
Paso 7: El punto donde se cruzan dos bisectrices perpendiculares es el centro del círculo. Márcalo como el punto O. Por lo tanto, O es el centro del círculo dado.

Ejemplo 2: Dibuja diferentes pares de círculos. ¿Cuántos puntos tiene cada par en común? ¿Cuál es el número máximo de puntos comunes? 

Solución :

(i) Ningún punto común:

(ii) Un punto común:

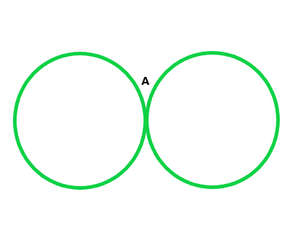
(iii) Dos puntos comunes:

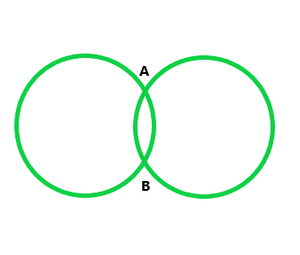
Como podemos analizar desde arriba, dos círculos pueden cortarse como máximo en dos puntos .