Teorema – Las longitudes de las tangentes trazadas desde un punto externo a un círculo son iguales – Círculos | Clase 10 Matemáticas

La tangente es una línea recta trazada desde un punto externo que toca un círculo exactamente en un punto de la circunferencia del círculo. Puede haber un número infinito de tangentes de un círculo. Estas tangentes siguen ciertas propiedades que pueden usarse como identidades para realizar cálculos matemáticos en círculos.

Aquí, en este artículo, aprenderemos sobre una de esas propiedades, es decir, las tangentes dibujadas desde un punto externo a un círculo tienen la misma longitud.

Para probar: las longitudes de las tangentes dibujadas desde un punto externo a un círculo son iguales 

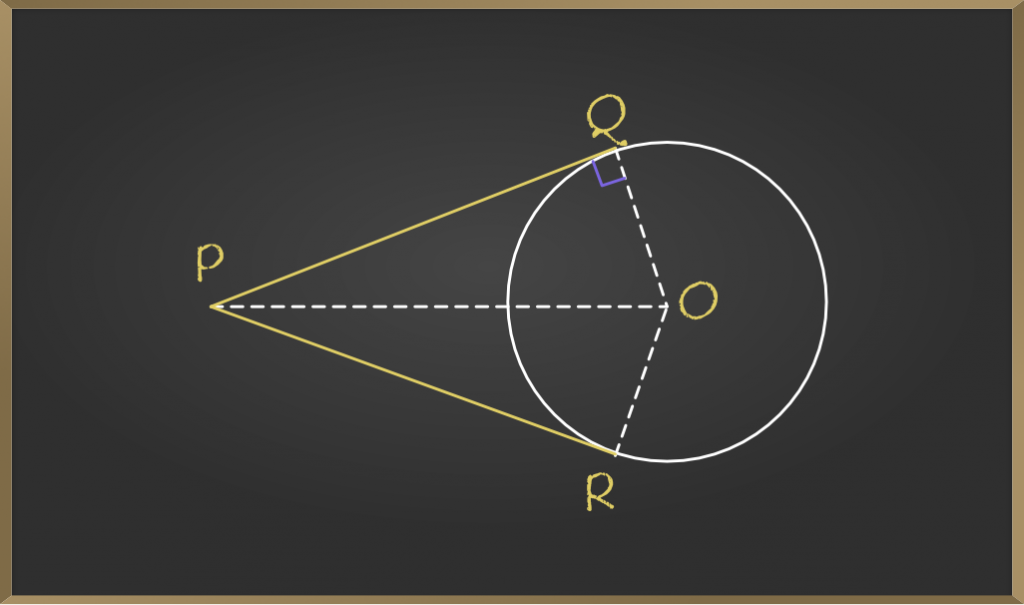
Sean PQ y PR las dos tangentes trazadas a la circunferencia de Centro O como se muestra en la figura. 

Construcción

Dibuje un segmento de línea, desde el centro O hasta el punto externo P {es decir, P es el punto de intersección de ambas tangentes} 

Ahora ∆POR y ∆POQ . 

Para probar que tienen la misma longitud, primero probaremos que ambos triángulos son semejantes. 

Sabemos que las tangentes forman un ángulo recto con un radio del círculo. 

Aquí, OR y OQ es el radio del círculo

Entonces, ∠OQP = ∠ORP = 90°
Ahora, está claro que ambos triángulos ∆POQ y ∆POR son triángulos rectángulos y una hipotenusa OP común en ellos. 

Prueba

Ahora demostrando la similitud entre los triángulos ∆POQ y ∆POR

Aquí,

∠PQO = ∠PRO = 90° 
Hipotenusa común OP entre ellos. 

Y OQ = OR [Radio del círculo]. 
Entonces, por la regla de similitud de RHS 

∆POQ ~ ∆POR 

Por lo tanto, ambos triángulos son similares entre sí. 

Por lo tanto, 
OP/OP = PQ/PR = OQ/OR 

PQ/PR = 1 {ya que OP/OP = 1} ; 

Por lo tanto, PQ = PR; 

Por lo tanto, demostró que las longitudes de las tangentes dibujadas desde un punto externo a un círculo son iguales. 

Ejemplos de problemas basados ​​en el teorema

Problema 1: Se trazan dos tangentes desde un punto exterior sobre una circunferencia de 3 cm de área. Halla el área del cuadrilátero formado por los dos radios de la circunferencia y dos tangentes si la distancia entre el centro de la circunferencia y el punto exterior es de 5 cm. 

Solución:

Se toma en cuenta que si se une PO, entonces ΔPQO será un ángulo recto en Q, por lo que se aplica el Teorema de Pitágoras : 

Dado que: 
OQ = 3 cm 
OP = 5 cm 
Usando Pitágoras podemos encontrar el OP: 
OP^2 = OQ^2 + PQ^2 
25 = 9 + QP^2 
Qp = 4 cm. 

Dado que ambas, las tangentes tienen la misma longitud y también sabemos que los triángulos son congruentes, por lo tanto, ambos triángulos tendrían la misma área. 

Por lo tanto, 

Área total = 2 veces el área del triángulo 
Área = 2 * (1/2) * 4 * 3 
Área = 12 cm^2 

Por lo tanto, el área total es de 12 cm^2. 

Problema 2: ¿Cuántas tangentes se pueden trazar a la circunferencia S desde un punto P dentro de la circunferencia S? Explique sus hallazgos. 

Solución: 

La respuesta es ninguna. Pero lo importante aquí es la explicación. 
Supongamos que si PA es una tangente al círculo S desde un punto interno P, entonces los puntos P, O y A formarán un triángulo rectángulo con hipotenusa OP. 
Sabemos que OA es un radio del círculo S, ya que P está dentro de S, OP debe ser menor que OA (por la regla de la hipotenusa en un triángulo rectángulo). Por lo tanto, el triángulo supuesto anteriormente no puede existir. 
Por lo tanto, se demostró que no se puede trazar una tangente desde un punto interior P al círculo S. 

Problema 3: Se inscribe una circunferencia en el cuadrilátero ABCD, probar que AB + CD = AD + BC. 
La figura se proporciona para su referencia. 

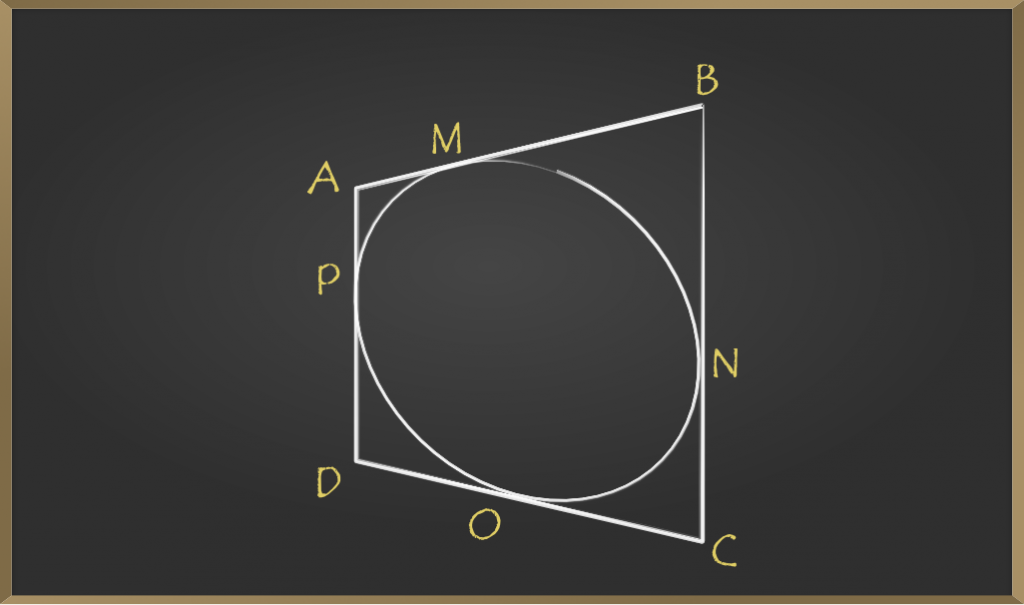
Solución:

Ya sabemos que la longitud de las tangentes trazadas desde el punto A será la misma. 
De esto, inferimos que, 
AP = AM —(1) 

Análogamente, para tangentes trazadas desde el punto B, 
BN = BM —(2) 

De la misma manera para las Tangentes trazadas desde el punto C, 
CN = CO —(3) 

De la misma manera para las Tangentes trazadas desde el punto D, 
DP = DO —(4) 

Sumando las ecuaciones (1),(2), (3),(4), 
tenemos: 
AM + BM + CO + DO = AP + BN + CN + DP 

Ahora; 
⇒ AP + PD + BN + NC = AM + MB + DO + OC 
⇒ AD + BC = AB + CD 

Por lo tanto probado. 

Problema 4: Desde un punto exterior B se trazan las tangentes BC y BD a una circunferencia de centro A de manera que la longitud de cada tangente sea 4 cm y AB = 5 cm. Cual es el radio del circulo? 

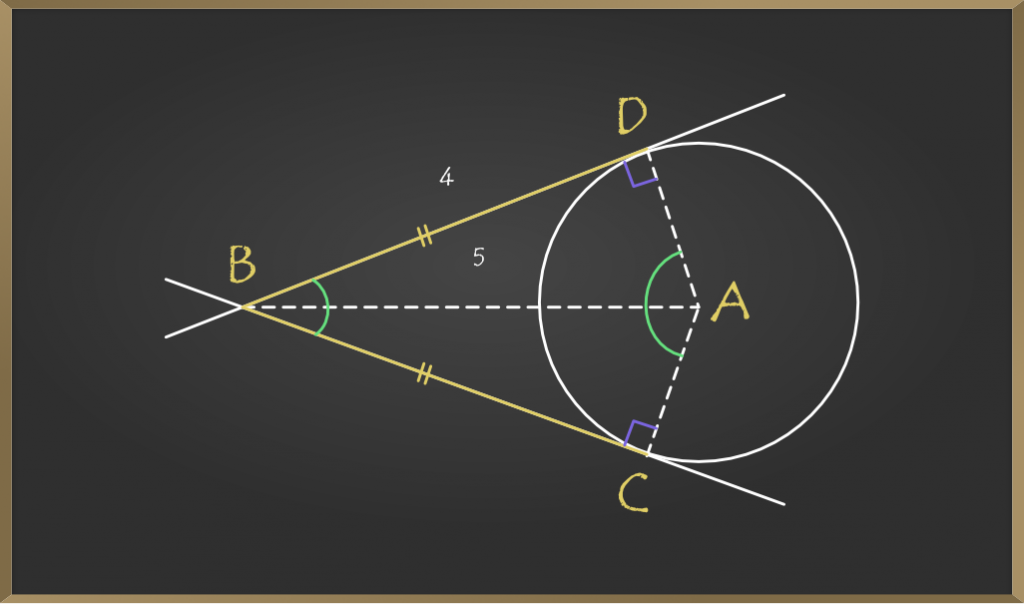
Solución:

Se toma en cuenta que si se une AB, entonces ΔABC será un ángulo recto en C, por lo que se aplica el Teorema de Pitágoras : 

AB ² = AC ² + BC ² 
AC ² = AB ² – BC ² = 25 – 16 = 9

Por lo tanto, CA = 3