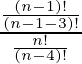Teorema 1 : El número de permutaciones de n objetos diferentes tomados r a la vez, donde 0 < r ≤ n y los objetos no se repiten es
n(n-1)(n-2). . .(n – r + 1), que se denota por n P r =
Teorema 2: El número de permutaciones de n objetos diferentes tomados r a la vez, donde se permite la repetición, es n r .
Teorema 3: El número de permutaciones de n objetos, donde p objetos son del mismo tipo y el resto son todos diferentes
=
Teorema 4: El número de permutaciones de n objetos, donde P 1 objetos son de una clase, P 2 son de segunda clase, …, P k son de k ésima clase y el resto, si los hay, son de diferente clase es
=
Pregunta 1. ¿Cuántos números de 3 dígitos se pueden formar usando los dígitos del 1 al 9 si no se repite ningún dígito?
Solución:
Como vemos aquí, hemos dado 9 dígitos diferentes, y tenemos que seleccionar 3 de ellos para formar un número de tres dígitos, y no se permite la repetición.
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá tantos números de 3 dígitos como permutaciones de 9 dígitos diferentes tomados de 3 a la vez.
= 9 P 3
=
=
= 9×8×7
= 504
Por lo tanto, podemos formar 504 números de tres dígitos.
Solución alternativa: Teorema de la multiplicación
Como en este caso, no se permite la repetición. Aquí, si el lugar de la unidad se llena primero, se puede llenar con cualquiera de los nueve dígitos dados. Entonces, el número de formas de llenar el lugar de las unidades del número de tres dígitos es 9.
Luego, el lugar de las decenas se puede llenar con cualquiera de los ocho dígitos restantes y el lugar de las centenas se puede llenar con cualquiera de los siete dígitos restantes.
9 maneras 8 maneras 7 maneras Por lo tanto, por el principio de la multiplicación, el número de formas en que se pueden formar números de tres dígitos sin repetir son:
= 9×8×7
= 504
Pregunta 2. ¿Cuántos números de 4 dígitos hay sin dígito repetido?
Solución:
Como sabemos, tenemos 10 dígitos diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9) y tenemos que seleccionar 4 de ellos para formar un número de cuatro dígitos, y la repetición es No permitido.
PERO , como sabemos, no podemos colocar 0 en el lugar de los miles (porque entonces el número no será un número de cuatro dígitos). Así que calcularemos la permutación de los tres lugares restantes por separado y los miles de lugares por separado.
Para el lugar de los miles: tenemos 9 dígitos diferentes (excluyendo el 0) y tenemos que seleccionar 1 de ellos.
y, Para los tres lugares restantes: nos quedan 9 dígitos diferentes (incluido el 0) y tenemos que seleccionar 3 de ellos.
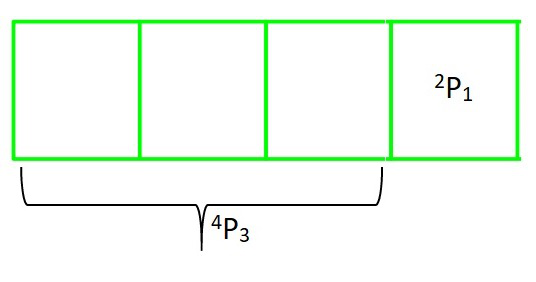
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá tantos números de 4 dígitos como permutaciones de (9 dígitos diferentes tomando 1 a la vez) y (9 dígitos diferentes tomando 3 a la vez).
= 9 PAGS 1 × 9 PAGS 3
=
=
= 9×9×8×7
= 4536
Por lo tanto, podemos formar 4536 números de cuatro dígitos.
Solución alternativa: Teorema de la multiplicación
Como en este caso, no se permite la repetición. Aquí, el lugar de los millares del número de 4 dígitos debe llenarse primero con cualquiera de los dígitos del 1 al 9 (no se puede incluir el 0). Por lo tanto, el número de formas en que se puede llenar el lugar de los millares es 9 .
Entonces, el lugar de las centenas se puede llenar con cualquiera de los dígitos del 0 al 9. Como el dígito no se puede repetir en los números de 4 dígitos y el lugar de los millares ya está ocupado con un dígito. Luego, estos lugares restantes deben completarse con los 9 dígitos restantes.
Luego, el lugar de las decenas se puede llenar con cualquiera de los ocho dígitos restantes y el lugar de las centenas se puede llenar con cualquiera de los siete dígitos restantes.
9 maneras 9 maneras 8 maneras 7 maneras Por lo tanto, por el principio de la multiplicación, el número de formas en que se pueden formar números de tres dígitos sin repetir son:
= 9×9×8×7
= 4536
Pregunta 3. ¿Cuántos números pares de 3 dígitos se pueden formar con los dígitos 1, 2, 3, 4, 6, 7 si no se repite ningún dígito?
Solución:
Como sabemos, tenemos 6 dígitos diferentes (1, 2, 3, 4, 6 y 7) y tenemos que seleccionar 3 de ellos para formar un número de tres dígitos, y no se permite la repetición.
PERO como sabemos, tenemos que colocar un número par en el lugar de las unidades (porque entonces el número debe ser un número par de tres dígitos). Entonces calcularemos la permutación de los dos lugares restantes por separado y los lugares por separado.
Para el lugar de las unidades: tenemos 3 dígitos diferentes, y tenemos que seleccionar 1 de ellos.
y, Para los dos lugares restantes: nos quedan 5 dígitos diferentes, y tenemos que seleccionar 2 de ellos.
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá tantos números pares de 3 dígitos como permutaciones de (3 dígitos diferentes tomados de 1 a la vez) y (5 dígitos diferentes tomados de 2 a la vez).
= 3 PAGS 1 × 5 PAGS 2
=
=
= 3×5×4
= 60
Por lo tanto, podemos formar 60 números de tres dígitos.
Solución alternativa: Teorema de la multiplicación
Como en este caso, no se permite la repetición. Aquí, el lugar de las unidades del número de 3 dígitos debe llenarse primero con cualquier número par de los dígitos de 2, 4 y 6 ( el número será par al terminar en 2, 4 y 6 ). Por lo tanto, el número de formas en que el lugar de uno se puede llenar es 3.
Luego, los lugares de las decenas y las centenas se pueden llenar con cualquiera de los dígitos restantes. Como el dígito no se puede repetir en los números de 3 dígitos y el lugar de las unidades ya está ocupado con un dígito. Luego, los lugares restantes de decenas y centenas se deben completar con los 5 y 4 dígitos restantes, respectivamente.
3 formas 5 maneras 4 formas Por lo tanto, por el principio de la multiplicación, el número de formas en que se pueden formar números de tres dígitos sin repetir son:
= 3×5×4
= 60
Pregunta 4. Encuentra la cantidad de números de 4 dígitos que se pueden formar usando los dígitos 1, 2, 3, 4, 5 si no se repite ningún dígito. ¿Cuántos de estos serán pares?
Solución:
Como vemos aquí, hemos dado 5 dígitos diferentes, y tenemos que seleccionar 4 de ellos para formar un número de cuatro dígitos, y no se permite la repetición.
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá tantos números de 4 dígitos como permutaciones de 5 dígitos diferentes tomados de 4 a la vez.
= 5 P 4
=
=
= 5×4×3×2×1
= 120
Por lo tanto, podemos formar 120 números de cuatro dígitos.
¿Para números pares?
Como sabemos, tenemos 5 dígitos diferentes (1, 2, 3, 4 y 5) y tenemos que seleccionar 4 de ellos para formar un número de cuatro dígitos, y no se permite la repetición.
PERO , como sabemos, tenemos que colocar un número par en el lugar de las unidades (porque entonces el número debe ser un número par de cuatro dígitos). Entonces calcularemos la permutación de los tres lugares restantes y los lugares por separado.
Para el lugar de las unidades: tenemos 2 dígitos diferentes, y tenemos que seleccionar 1 de ellos.
y, Para los tres lugares restantes: nos quedan 4 dígitos diferentes, y tenemos que seleccionar 3 de ellos.
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá tantos números pares de 4 dígitos como permutaciones de (2 dígitos diferentes tomando 1 a la vez) y (4 dígitos diferentes tomando 3 a la vez).
= 2 PAGS 1 × 4 PAGS 3
=
=
= 2×4×3×2
= 48
Por lo tanto, podemos formar 48 números pares de cuatro dígitos
Solución alternativa: Teorema de la multiplicación
Como en este caso, no se permite la repetición. Aquí, el lugar de las unidades del número de 4 dígitos debe llenarse primero con cualquier número de los dígitos del 1 al 5. Por lo tanto, el número de formas en que se puede llenar el lugar de las unidades es 5.
Luego, los lugares de las decenas, centenas y centenas se pueden llenar con cualquiera de los dígitos restantes. Como el dígito no se puede repetir en los números de 4 dígitos y el lugar de las unidades ya está ocupado con un dígito. Luego, las decenas, centenas y miles de lugares restantes se llenarán con los 4, 3 y 2 dígitos restantes respectivamente.
5 maneras 4 formas 3 formas 2 maneras Por lo tanto, por el principio de la multiplicación, el número de formas en que se pueden formar números de cuatro dígitos sin repetir son:
= 5×4×3×2
= 120
¿Para números pares?
Como en este caso, no se permite la repetición. Aquí, el lugar de las unidades del número de 4 dígitos debe llenarse primero con cualquier número par de los dígitos del 2 y el 4 (el número será par al terminar en 2 y 4). Por lo tanto, el número de formas en que el lugar de las unidades puede ser lleno es 2.
Luego, los lugares de las decenas, centenas y centenas se pueden llenar con cualquiera de los dígitos restantes. Como el dígito no se puede repetir en los números de 4 dígitos y el lugar de las unidades ya está ocupado con un dígito. Luego, las decenas, centenas y miles de lugares restantes se llenarán con los 4, 3 y 2 dígitos restantes respectivamente.
2 maneras 4 formas 3 formas 2 maneras Por lo tanto, por el principio de la multiplicación, el número de formas en que se pueden formar números pares de cuatro dígitos sin repetirse son:
= 2×4×3×2
= 48
Pregunta 5. De un comité de 8 personas, ¿de cuántas maneras podemos elegir un presidente y un vicepresidente suponiendo que una persona no puede ocupar más de un cargo?
Solución:
Como vemos aquí, hay 8 personas diferentes, y tenemos que seleccionar 2 de ellos para formar un comité y no se permite la repetición (una persona no puede ocupar más de un puesto).
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, se pueden formar tantos comités como permutaciones de 8 personas tomadas 2 a la vez.
= 8 P 2
=
=
= 8×7
= 56
Por lo tanto, podemos formar 56 comités de dos personas.
Solución alternativa: Teorema de la multiplicación
Como en este caso, una misma persona no puede ocupar más de un cargo. Aquí si elegimos primera persona, Entonces, el número de formas que tenemos es 8.
Entonces, si elegimos la segunda persona, como la primera persona ya está seleccionada, entonces, el número de formas que tenemos es 7.
8 maneras 7 maneras De ahí, por principio de multiplicación, el número de formas en que se puede formar un comité de dos personas:
= 8×7
= 56
Pregunta 6. Encuentra n si, n –1 P 3 : n P 4 = 1 : 9.
Solución:
Dado.
n –1 P 3 / n P 4 =
………………………………….(1)
como n P r =
n –1 P 3 / n P 4 =
=
(cancelando (n-4)!))
=
=
(n! = n × (n-1)!)
=
(cancelando (n-1)!))
Por simplificación (1) obtenemos,
Por lo tanto, n = 9
Pregunta 7. Encuentra r si
(i) 5 P r = 2 6 P r−1
(ii) 5 P r = 6 P r−1
Solución:
(i) Dado.
5 PAGS r = 2 6 PAGS r−1
como n P r =
Asi que,
¡Al cambiar (7-r)! a la LHS y 5! al RHS obtenemos,
= 2 (6) ((7-r)! = (7-r) (7-r-1) (7-r-2)! = (7-r) (6-r) (5-r)!
(7-r) (6-r) = 2 (6) ………………………(1) (anulando (5-r)!))
Por simplificación (1) obtenemos,
42-6r- 7r+r 2 = 12
r2-13r + 30=0
r 2 -10r-3r+30=0
r(r-10)-3(r-10) = 0
(r-3) (r-10) = 0
Entonces r=3 y r=10
en n P r , r siempre es 0<r≤n
Así que aquí, 0<r≤5
r=3 y r≠10
Por lo tanto, r=3
(ii) Dado.
5 PAGS r = 6 PAGS r−1
como n P r =
Asi que,
¡Al cambiar (7-r)! a la LHS y 5! al RHS obtenemos,
= 6 ((7-r)! = (7-r) (7-r-1) (7-r-2)! = (7-r) (6-r) (5-r)!
(7-r) (6-r) = 6) ………………………(1) (anulando (5-r)!))
Por simplificación (1) obtenemos,
42-6r- 7r+r 2 = 6
r2-13r + 36=0
r 2 -9r-4r+36=0
r(r-9)-4(r-9) = 0
(r-9) (r-4) = 0
Entonces r=9 y r=4
en n P r , r siempre es 0<r≤n
Así que aquí, 0<r≤5
r=4 y r≠9
Por lo tanto, r=4
Pregunta 8. ¿Cuántas palabras, con o sin significado, se pueden formar usando todas las letras de la palabra ECUACIÓN, usando cada letra exactamente una vez?
Solución:
Como vemos aquí, hay 8 letras diferentes, y tenemos que formar palabras de 8 letras usando estas letras y no se permite la repetición (usando cada letra exactamente una vez).
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá permutaciones de 8 letras diferentes tomadas de 8 a la vez.
= 8 P 8
=
=
= 8!
= 8×7×6×5×4×3×2×1
= 40320
Por lo tanto, podemos formar 40320 palabras.
Pregunta 9. ¿Cuántas palabras, con o sin significado, se pueden formar con las letras de la palabra LUNES, suponiendo que no se repita ninguna letra, si.
(i) se utilizan 4 letras a la vez,
(ii) todas las letras se utilizan a la vez,
(iii) ¿se usan todas las letras pero la primera letra es una vocal?
Solución:
LUNES tiene 6 letras diferentes.
(i) Como vemos aquí, hay 6 letras diferentes, y tenemos que formar palabras de 4 letras usando estas letras y no se permite la repetición.
Entonces, de acuerdo con el Teorema 1: Por lo tanto, habrá permutaciones de 6 letras diferentes tomadas de 4 a la vez.
= 6 P 4
=
=
= 6×5×4×3
= 360
Por lo tanto, podemos formar 360 palabras.
(ii) Como vemos aquí, hay 6 letras diferentes y tenemos que formar una palabra de 6 letras usando estas letras y no se permite la repetición.
Entonces, de acuerdo con el Teorema 1: Por lo tanto, habrá permutaciones de 6 letras diferentes tomadas de 6 a la vez.
= 6 P 6
=
=
= 6×5×4×3×2×1
= 720
Por lo tanto, podemos formar 720 palabras.
(iii) Como sabemos, tenemos 6 letras diferentes y tenemos que seleccionar 6 de ellas ya que se usan todas las letras pero la primera letra es una vocal y no se permite la repetición.
PERO como sabemos tenemos que colocar una vocal en primer lugar. Entonces calcularemos la permutación de los 5 lugares restantes y 1 lugar por separado.
Para el primer puesto: tenemos 2 letras diferentes, y tenemos que seleccionar 1 de ellas.
y, Para los lugares restantes: nos quedan 5 letras diferentes, y tenemos que seleccionar 5 de ellas.
Entonces, de acuerdo con el Teorema 1 : Por lo tanto, habrá tantas palabras de 6 letras como permutaciones de (2 letras diferentes tomadas 1 a la vez) y (5 letras diferentes tomadas 5 a la vez).
= 2 PAGS 1 × 5 PAGS 5
=
=
= 2×5×4×3×2×1
= 240
Por lo tanto, podemos formar 240 palabras.
Pregunta 10. ¿En cuántas de las distintas permutaciones de las letras en MISSISSIPPI se juntan las cuatro I’s not?
Solución:
MISSISSIPPI tiene 11 letras donde,
Carta Veces METRO 1 yo 4 S 4 PAGS 2 Entonces, de acuerdo con el Teorema 4 : Por lo tanto, habrá tantas palabras de 11 letras como permutaciones de 11 letras tomadas 11 a la vez con algunas palabras repetidas.
= 11 P 11 /(1! 4! 4! 2!)
=
=
(¡cancelando 4!)
No. de permutaciones distintas de las letras = 34650
Ahora, como hay 4 I en la palabra dada. Cuando ocurren juntos, se tratan como un solo objeto por el momento.
yo yo yo yo Por lo tanto, número total de palabras = 11-4+1 = 8
Entonces, de acuerdo con el Teorema 4: Por lo tanto, habrá tantas palabras de 8 letras como permutaciones de 8 letras tomadas de 8 a la vez que tengan algunas palabras repetidas.
= 8 P 8 /(1! 4! 2!)
=
=
(¡cancelando 4!)
= 840
Por lo tanto, distintas permutaciones de las letras en MISSISSIPPI donde cuatro I no se juntan = 34650 – 840
= 33810
Pregunta 11. ¿De cuántas maneras se pueden ordenar las letras de la palabra PERMUTACIONES si la
(i) las palabras comienzan con P y terminan con S,
(ii) las vocales están todas juntas,
(iii) siempre hay 4 letras entre P y S?
Solución:
PERMUTACIONES tiene 12 letras, donde la repetición de ‘T’ 2 veces.
(i) La primera y la última letra se fijan como P y S respectivamente.
entonces 12-2 = quedan 10 letras.
Entonces, de acuerdo con el Teorema 4 : Por lo tanto, habrá tantas palabras de 12 letras como permutaciones de 10 letras tomadas de 10 a la vez que tengan algunas palabras repetidas.
= 10 P 10 /2!
=
= 10×9×8×7×6×5×4×3
= 1814400
(ii) No. de vocales en PERMUTACIONES (E, U, A, I, O) = 5
mi tu A yo O Ahora considerando todas las vocales juntas como un solo objeto.
Número total de letras = 12-5+1 = 8
Entonces, de acuerdo con el Teorema 4: Por lo tanto, habrá tantas palabras de 8 objetos como permutaciones de 8 objetos tomados de 8 a la vez que tengan algunas palabras repetidas.
= 8 P 8 /2!
=
Usando el principio de multiplicación, el número de disposición de las vocales será:
=
= 2419200
(iii) Como debe haber 4 letras entre P y S.
Entonces, se fijan dos lugares para P y S.
entonces 12-2 = quedan 10 letras.
Entonces, de acuerdo con el Teorema 4: Por lo tanto, habrá tantas palabras de 12 letras como permutaciones de 10 letras tomadas de 10 a la vez que tengan algunas palabras repetidas.
= 10 P 10 /2!
=
Como hay 14 formas posibles de colocar P y S entre 4 letras.
Colocando en (1 y 6), (6 y 1), (2 y 7), (7 y 2), (3 y 8), (8 y 3), (4 y 9) y (9 y 4), (5 y 10), (10 y 5), (11 y 6), (6 y 11), (12 y 7) y (7 y 12) posiciones.
Por lo tanto, hay =
×14
= 25401600
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA