Demuestre lo siguiente usando el principio de inducción matemática para todo n ∈ N:
Pregunta 1: 1 + 3 + 3 2 + …….. + 3 n-1 = 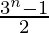
Solución:
Tenemos,
P(n) = 1 + 3 + 3 2 + …….. + 3 n-1 =
Para n=1 , obtenemos
P(1) = 1 =
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1 + 3 + 3 2 + …….. + 3 k-1 =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1 + 3 + 3 2 + …….. + 3 k-1 + 3 (k+1)-1
= (1 + 3 + 3 2 + …….. + 3 k-1 ) + 3 k
De la ecuación (1), obtenemos
=
+ 3k
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 2: 1 + 2 3 + 3 3 + ……….. + n 3 = ![Procesado por QuickLaTeX.com [\frac{n(n+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-503895ebcf6131d03275e7171f4e28c8_l3.png)
Solución:
Tenemos,
P(n) = 1 + 2 3 + 3 3 + ……….. + n 3 =
Para n=1 , obtenemos
P(1) = 1 =
= 1
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1 + 2 3 + 3 3 + ……….. + k 3 =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1 + 2 3 + 3 3 + ……….. + k 3 + (k+1) 3
= (1 + 2 3 + 3 3 + ……….. + k 3 ) + (k+1) 3
De la ecuación (1), obtenemos
=
+ (k+1) 3
=
+ (k+1) 3
=
Tomando (k+1) 2 , obtenemos
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 3: 1 +  + ……. +
+ ……. +  =
= 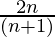
Solución:
Tenemos,
P(n) = 1 +
=
Para n=1 , obtenemos
P(1) = 1 =
= 1
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1 +
=
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1 +
+
= (1 +
) +
De la ecuación (1), obtenemos
=
Como sabemos que,
Suma del primer número natural,
1 + 2 + 3 + …… + norte =
Entonces, obtenemos
=
=
=
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 4: 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) = 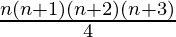
Solución:
Tenemos,
P(n) = 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) =
Para n=1 , obtenemos
P(1) = 1.2.3 =
=
= 1.2.3
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1.2.3 + 2.3.4 +…+ k(k+1) (k+2) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1.2.3 + 2.3.4 +…+ k(k+1) (k+2) + (k+1)(k+1+1) (k+1+2)
= (1.2.3 + 2.3.4 +…+ k(k+1) (k+2)) + (k+1)(k+2) (k+3)
De la ecuación (1), obtenemos
=
+ (k+1)(k+2)(k+3)
= (k+1)(k+2) (k+3) (
+ 1)
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 5: 1.3 + 2.3 2 + 3.3 3 +…+ n.3 n = 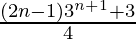
Solución:
Tenemos,
P(n) = 1.3 + 2.3 2 + 3.3 3 +…+ n.3 n =
Para n=1 , obtenemos
P(1) = 1,3 = 3 =
= 3
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1.3 + 2.3 2 + 3.3 3 +…+ k.3 k =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1.3 + 2.3 2 + 3.3 3 +…+ k.3 k + (k+1).3 (k+1)
= (1.3 + 2.3 2 + 3.3 3 +…+ k.3 k ) + (k+1).3 (k+1)
De la ecuación (1), obtenemos
=
+ (k+1).3 (k+1)
=
= 3k+1
= 3k+1
= 3k+1
= 3 (k+1)+1
Por eso,
P(k+1) = 3 (k+1)+1
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 6: 1.2 + 2.3 + 3.4 +…+ n.(n+1) = ![Rendered by QuickLaTeX.com [\frac{n(n+1)(n+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69de8a069d88755a83c28347803392ca_l3.png)
Solución:
Tenemos,
P(n) = 1,2 + 2,3 + 3,4 +…+ n.(n+1) =
Para n=1 , obtenemos
P(1) = 1,2 = 2 =
= 2
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1.2 + 2.3 + 3.4 +…+ k.(k+1) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1,2 + 2,3 + 3,4 +…+ k.(k+1) + (k+1)(k+1+1)
= (1.2 + 2.3 + 3.4 +…+ k.(k+1)) + (k+1)(k+2)
De la ecuación (1), obtenemos
=
+ (k+1)(k+2)
=
= (k+1)(k+2)
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 7: 1,3 + 3,5 + 5,7 +…+ (2n–1) (2n+1) =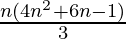
Solución:
Tenemos,
P(n) = 1,3 + 3,5 + 5,7 +…+ (2n–1) (2n+1) =
Para n=1 , obtenemos
P(1) = 1,3 = 3 =
=
= 3
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1,3 + 3,5 + 5,7 +…+ (2k–1) (2k+1) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1,3 + 3,5 + 5,7 +…+ (2k–1) (2k+1) + (2(k+1)-1)(2(k+1)+1)
= (1,3 + 3,5 + 5,7 +…+ (2k–1) (2k+1)) + (2k+1)(2k+3)
De la ecuación (1), obtenemos
=
+ (4k 2 +8k+3)
=
=
=
=
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 8: 1.2 + 2.2 2 + 3.2 3 + …+n.2 n = (n–1) 2 n + 1 + 2
Solución:
Tenemos,
P(n) = 1.2 + 2.2 2 + 3.2 3 + …+n.2 n = (n–1) 2 n + 1 + 2
Para n=1 , obtenemos
P(1) = 1,2 = 2 = (1–1) 2(1) + 1 + 2 = 2
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1.2 + 2.2 2 + 3.2 3 + …+k.2 k = (k–1) 2 k + 1 + 2 ……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1.2 + 2.2 2 + 3.2 3 + …+k.2 k + (k+1).2 (k+1)
= (1.2 + 2.2 2 + 3.2 3 + …+k.2 k ) + (k+1).2 (k+1)
De la ecuación (1), obtenemos
= (k–1) 2k + 1 + 2 + (k+1).2k +1
= 2 k + 1 ((k–1) + (k+1)) + 2
= 2k + 1(2k) + 2
= k.2 k+1+1 + 2
= ((k+1)-1).2 (k+1)+1 + 2
Por eso,
P(k+1) = ((k+1)-1).2 (k+1)+1 + 2
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 9: 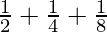 + …… +
+ …… + 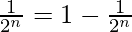
Solución:
Tenemos,
P(n) =
Para n=1 , obtenemos
P(1) =
= 1 –
=
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
= (
) +
De la ecuación (1), obtenemos
= 1 –
= 1 –
= 1 –
= 1 –
= 1 –
Por eso,
P(k+1) = 1 –
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 10:  + …… +
+ …… + 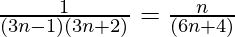
Solución:
Tenemos,
P(n) =
Para n=1 , obtenemos
P(1) =
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
= (
) +
De la ecuación (1), obtenemos
=
=
=
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 11: 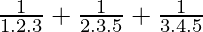 + …… +
+ …… + 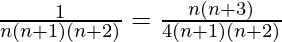
Solución:
Tenemos,
P(n) =
Para n=1 , obtenemos
P(1) =
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
= (
) +
De la ecuación (1), obtenemos
=
=
=
=
=
=
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 12: a + ar + ar 2 + …… + ar n-1 = 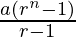
Solución:
Tenemos,
P(n) = a + ar + ar 2 + …… + ar n-1 =
Para n=1, obtenemos
P(1) = un =
= un
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = a + ar + ar 2 + …… + ar k-1 =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = a + ar + ar 2 + …… + ar k-1 + ar (k+1)-1
= (a + ar + ar 2 + …… + ar k-1 ) + ar k
De la ecuación (1), obtenemos
=
+ ark
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 13: (1+ 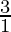 ) (1+
) (1+ 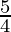 ) (1+
) (1+ 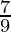 ) ….. (1+
) ….. (1+ 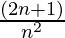 ) = (n+1) 2
) = (n+1) 2
Solución:
Tenemos,
P(n) =
= (n+1) 2
Para n=1 , obtenemos
P(1) = 1+
= 1+3 = 4 = (1+1) 2 = 2 2 = 4
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
= (k+1) 2 ……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
=
De la ecuación (1), obtenemos
= (k+1) 2 (1+
)
= (k+1) 2
= (k+1) 2 + 2(k+1) + 1
= {(k+1)} 2
Por eso,
P(k+1) = {(k+1)} 2
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.