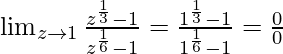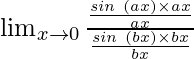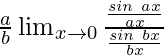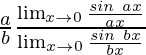Evalúe los siguientes límites en los ejercicios 1 a 22.
Pregunta 1: 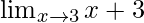
Solución:
En
, como x⇢3
Ponga x = 3, obtenemos
= 3+3
= 6
Pregunta 2: 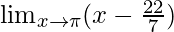
Solución:
En
, como x⇢π
Ponga x = π, obtenemos
=
Pregunta 3: 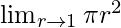
Solución:
En
, como r⇢1
Ponga r = 1, obtenemos
= π
Pregunta 4: 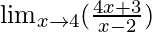
Solución:
En
, como x⇢4
Ponga x = 4, obtenemos
=
Pregunta 5: 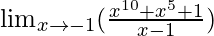
Solución:
En
, como x⇢-1
Ponga x = -1, obtenemos
=
=
Pregunta 6: 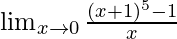
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, tomemos x+1=p y x = p-1, para hacerlo equivalente al teorema.
Como, x⇢0 ⇒ p⇢1
Aquí, n=5 y a = 1.
= 5(1) 4
= 5
Pregunta 7: 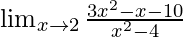
Solución:
En
, como x⇢2
Ponga x = 2, obtenemos
Como, este límite se vuelve indefinido.
Ahora, factoricemos el numerador y el denominador, obtenemos
=
Cancelando (x-2), tenemos
=
Ponga x = 2, obtenemos
=
Pregunta 8: 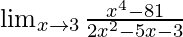
Solución:
En
, como x⇢3
Ponga x = 3, obtenemos
Como, este límite se vuelve indefinido.
Ahora, factoricemos el numerador y el denominador, obtenemos
=
=
Cancelando (x-3), tenemos
=
Ponga x = 3, obtenemos
=
=
=
Pregunta 9: 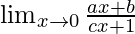
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
= segundo
Pregunta 10: 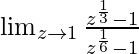
Solución:
En
, como z⇢1
Ponga z = 1, obtenemos
Tomemos
= p y
= p 2 ,
Como, z⇢1 ⇒ p⇢1
=
Ahora, factoricemos el numerador, obtenemos
=
Cancelando (p-1), tenemos
=
Ponga p = 1, obtenemos
= 2
Pregunta 11: 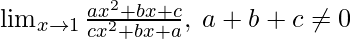
Solución:
En
, como x⇢1
Ponga x = 1, obtenemos
=
= 1 (Como se da a+b+c≠0)
Pregunta 12: 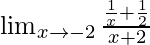
Solución:
En
, como x⇢-2
En primer lugar, simplifiquemos la ecuación
Cancelando (x+2), obtenemos
Ponga x = -2, obtenemos
=
Pregunta 13: 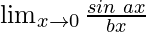
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, multipliquemos y dividamos la ecuación por a, para que sea equivalente al teorema.
Por lo tanto, tenemos
=
=
Como x⇢0, entonces ax⇢0
=
Usando el teorema, obtenemos
=
=
Pregunta 14: 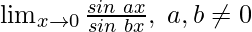
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, multipliquemos y dividamos el numerador por ax y el denominador por bx para que sea equivalente al teorema.
Por lo tanto, tenemos
=
=
Usando el teorema, obtenemos
=
=
Pregunta 15: 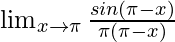
Solución:
En
, como x⇢π
Ponga x = π, obtenemos
Como, este límite se vuelve indefinido.
Ahora, tomemos π-x=p
Como, x⇢π ⇒ p⇢0
=
=
Usando el teorema, obtenemos
=
=
Pregunta 16: 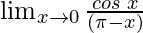
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
=
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA