Pregunta 1. Encuentra a, b y n en la expansión de (a + b) n si los primeros tres términos de la expansión son 729, 7290 y 30375, respectivamente.
Soluciones:
Como sabemos que (r+1) el término de (a+b) n se denota por,
T r+1 = norte C r un norte-r segundo r
Aquí, se da que los primeros tres términos de la expansión son 729, 7290 y 30375.
Cuando, T 1 = 729, T 2 = 7290 y T 3 = 30375
T 0+1 (r=0) = norte C 0 un norte-0 segundo 0 = un norte = 729 …………………(1)
T 1+1 (r=0) = norte C 1 un n-1 segundo 1 = na n-1 segundo = 7290 …………………(2)
T 2+1 (r=0) = n C 2 a n-2 b 2 =
a n-2 b 2 =
= 30375 …………………(3)
Dividiendo (1) y (2), obtenemos
na n-1-n b = 10
= 10 ……………………….(I)
Ahora, dividiendo (3) y (2), obtenemos
De (I), podemos sustituir
= 10 –
………………….(II)
Sustituyendo (II) en (I), obtenemos
= 10
= 10
norte =
norte = 6
Sustituyendo n = 6 en (1), obtenemos
un n = 729
un 6 = 729
un = 3
Sustituyendo a = 3 en (II), obtenemos
segundo =
b = 5
Por lo tanto, a = 3, b = 5 y n = 6
Pregunta 2. Encuentra a si los coeficientes de x 2 y x 3 en la expansión de (3 + ax) 9 son iguales.
Soluciones:
Como sabemos que (r+1) el término de (a+b) n se denota por,
T r+1 = norte C r un norte-r segundo r
Aquí, a = 3 y b = ax y n = 9.
T r+1 = 9 C r 3 9-r (ax) r
V r+1 = 9 C r
un r x r
T r+1 = 9 C r
Entonces, aquí si quieres la potencia de x 2 y x 3 . Entonces r=2 y r=3.
r = 2, T 2+1 =
r = 3, T 3+1 =
Coeficiente de x 2 = Coeficiente de x 3
un =
Por lo tanto, a =
Pregunta 3. Encuentra el coeficiente de x 5 en el producto (1 + 2x) 6 (1 – x) 7 usando el teorema del binomio.
Soluciones:
Para obtener el coeficiente de x 5 , expandamos ambos binomios para una comprensión más clara.
(1 + 2x) 6 = 6 C 0 + 6 C 1 (2x) + 6 C 2 (2x) 2 + 6 C 3 (2x) 3 + 6 C 4 (2x) 4 + 6 C 5 (2x) 5 + 6 C 6 (2x) 6
= 1 + 6 (2x) + 15 (2x) 2 + 20 (2x) 3 + 15 (2x) 4 + 6 (2x) 5 + (2x) 6
= 1 + 12x + 60x 2 + 160×3 + 240×4 + 192×5 + 64x 6
(1 – x) 7 = 7 C 0 – 7 C 1 (x) + 7 C 2 (x) 2 – 7 C 3 (x) 3 + 7 C 4 (x) 4 – 7 C 5 (x) 5 + 7 C 6 (x) 6 – 7 C 7 (x) 7
= 1 – 7x + 21x 2 – 35x 3 + 35x 4 – 21x 5 + 7x 6 – x 7
Ahora, el producto se verá de la siguiente manera
(1 + 2x) 6 (1 – x) 7 = (1 + 12 x + 60x 2 + 160 x 3 + 240 x 4 + 192 x 5 + 64x 6 ) (1 – 7x + 21x 2 – 35x 3 + 35x 4 – 21x 5 + 7x 6 – x 7 )
Aquí, lo que podemos ver es que x 5 se obtendrá cuando se multipliquen dos términos que tienen la suma de potencias de x como 5. Esos dos términos quedarán de la siguiente manera:
primer binomio segundo binomio 1er término _ 6to término _ 2do término _ 5to término _ 3er término _ 4to término _ 4to término _ 3er término _ 5to término _ 2do término _ 6to término _ 1er término _ Asi que,
Coeficiente de x 5 = (1)(-21) + (12)(35) + (60)(-35) + (160)(21) + (240)(-7) + (192)(1)
Coeficiente de x 5 = -21 + 420 – 2100 + 3360 – 1680 + 192
Coeficiente de x 5 = -21 + 420 – 2100 + 3360 – 1680 + 192
Coeficiente de x 5 = 171
Por lo tanto, el coeficiente de x 5 en la expresión (1+2x) 6 (1-x) 7 es 171.
Pregunta 4. Si a y b son enteros distintos, probar que a – b es factor de a n – b n , siempre que n sea un entero positivo.
[Sugerencia escriba an = (a – b + b) n y expanda]
Soluciones:
Para probar que (a – b) es un factor de (a n – b n ),
a n – b n = k (a – b) donde k es un número natural o constante.
a se puede escribir como = a – b + b
un norte = (a – b + b) norte = [(a – b) + b] norte
[(a – b) + b] norte = norte C 0 (a – b) norte + norte C 1 (a – b) n-1 segundo + ………. norte C n-1 (a – b)b n-1 + norte C norte segundo norte
un norte = (a – b) norte + norte (a – b) n-1 b + ………. norte C n-1 (a – b)b n-1 + b norte
Ahora, a n – b n será
un norte – segundo norte = [(a – b) norte + norte (a – b) n-1 segundo + ………. n C n-1 (a – b)b n-1 + b n ] – b n
un norte – segundo norte = (a – b) norte + norte (a – b) n-1 segundo + ………. n C n-1 (a – b)b n-1
Tomando (ab) común, tenemos
un norte – segundo norte = (a – b) [(a –b) n-1 + norte (a – b) n-2 b + …… + norte C n-1 b n-1 ]
un norte – segundo norte = (a – b) k
Donde k = [(a –b) n-1 + n (a – b) n-2 b + …… + n C n-1 b n-1 ] es un número natural
Por tanto, se prueba que a – b es un factor de a n – b n , donde n es un entero positivo
Pregunta 5. Evaluar.
Soluciones:
Usando el teorema del binomio, la expresión (a + b) 6 y (a – b) 6 , se puede expandir de la siguiente manera:
(a + b) 6 = 6 C0 a 6 + 6 C 1 a 5 b + 6 C 2 a 4 b 2 + 6 C 3 a 3 b 3 + 6 C 4 a 2 b 4 + 6 C 5 ab 5 + 6 do 6 segundo 6
(a – b) 6 = 6 C 0 a 6 – 6 C 1 a 5 b + 6 C 2 a 4 b 2 – 6 C 3 a 3 b 3 + 6 C 4 a 2 b 4 – 6 C 5 ab 5 + 6 C 6 b 6
Ahora agregándolos,
(a + b) 6 – (a – b) 6 = 6 C 0 a 6 + 6 C 1 a 5 b + 6 C 2 a 4 b 2 + 6 C 3 a 3 b 3 + 6 C 4 a 2 b 4 + 6 C 5 ab 5 + 6 C 6 b 6 – [ 6 C 0 a 6– 6 C 1 a 5 b + 6 C 2 a 4 b 2 – 6 C 3 a 3 b 3 + 6 C 4 a 2 b 4 – 6 C 5 ab 5 + 6 C 6 b 6 ]
(a + b) 6 – (a – b) 6 = 2[ 6 C 1 a 5 b + 6 C 3 a 3 b 3 + 6 C 5 ab 5 ]
Sustituyendo a = √3 y b = √2, obtenemos
(√3 + √2) 6 – (√3 – √2) 6 = 2 [6 (√3) 5 (√2) + 20 (√3) 3 (√2) 3 + 6 (√3) (√ 2) 5 ]
= 2 [54(√6) + 120 (√6) + 24 √6]
= 2 (√6) (198)
= 396 √6
Pregunta 6. Encuentra el valor de 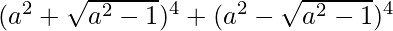 .
.
Soluciones:
Usando el teorema del binomio, la expresión (x+y) 4 y (x – y) 4 , se puede expandir de la siguiente manera:
(x + y) 4 = 4 C 0 x 4 + 4 C 1 x 3 y + 4 C 2 x 2 y 2 + 4 C 3 xy 3 + 4 C 4 y 4
(x – y) 4 = 4 C 0 x 4 – 4 C 1 x 3 y + 4 C 2 x 2 y 2 – 4 C 3 xy 3 + 4 C 4 y 4
Ahora agregándolos,
(x + y) 4 + (x – y) 4 = 4 C 0 x 4 + 4 C 1 x 3 y + 4 C 2 x 2 y 2 + 4 C 3 xy 3 + 4 C 4 y 4 + [ 4 C 0 x 4 – 4 C 1 x 3 y + 4 C 2 x 2 y 2 –4 C 3 xy 3 + 4 C 4 y 4 ]
(x + y) 4 + (x – y) 4 = 2[ 4 C 0 x 4 + 4 C 2 x 2 y 2 + 4 C 4 y 4 ]
Sustituyendo x = a 2 y y =
, obtenemos
= 2[a 8 + 6a 4 (a 2 -1) + (a 2 -1) 2 ]
= 2[a 8 + 6a 6 – 6a 4 + (a 4 + 1 – 2(a 2 )(1))]
= 2[a 8 + 6a 6 – 6a 4 + a 4 + 1 – 2a 2 ]
= 2a 8 + 12a 6 – 10a 4 – 4a 2 + 2
Pregunta 7. Encuentra una aproximación de (0.99) 5 usando los primeros tres términos de su desarrollo.
Soluciones:
Para hacer 0.99 en forma binomial,
0,99 = 1 – 0,01
Ahora, aplicando el teorema del binomio, obtenemos
(0. 99) 5 = (1 – 0.01) 5
Tomando los primeros tres términos de su expansión, tenemos
= 5 C 0 (1) 5 – 5 C 1 (1) 4 (0.01) + 5 C 2 (1) 3 (0.01) 2
= 1 – 5 (0,01) + 10 (0,01) 2
= 1 – 0,05 + 0,001
= 0,951
Aproximación de (0,99) 5 = 0,951.
Pregunta 8. Encuentra n, si la razón del quinto término desde el principio al quinto término desde el final en la expansión de ![Rendered by QuickLaTeX.com (\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d349518c28e352011d60762b42f7cca_l3.png) es √6:1.
es √6:1.
Soluciones:
Como, aquí se dice que tenemos que calcular
(Quinto término desde el principio: Quinto término desde el final) del Binomio =
En lugar de tomar el quinto término desde el final, invirtamos el término binomial y tomémoslo desde el principio.
Quinto término desde el final del binomio
= Quinto término desde el principio
Avancemos más con esto
Como sabemos que (r+1) el término de (a+b) n se denota por,
T r+1 = n Cr a n-r b r
Quinto término desde el principio de
,
T 5 = T 4+1 = norte C 4
T 5 = norte C 4
T 5 = norte C 4
T 5 = n C 4
…………………………….(1)
Ahora, Quinto término desde el principio de
,
T 5 = T 4+1 = norte C 4
T 5 = norte C 4
T 5 = norte C 4
T 5 = norte C 4
T 5 = n C 4
……………………….(2)
Ahora tomando la relación de (1) y (2), que es igual a √6:1
norte =
norte = 10
Pregunta 9. Expande usando el teorema del binomio 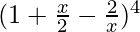 , x≠0.
, x≠0.
Soluciones:
Agrupando
en forma binomial, tenemos
Comparándolo con (a+b) n ,
a =
, b =
y n = 4
= 4 C 0
– 4 C 1
+ 4 C 2
– 4 C 3
+ 4 C 4
=
=
=
Ahora, obtengamos el valor de
y
= 3 C 0 (1) 3 + 3 C 1 (1) 2
+ 3 C 2 (1)
+ 3 C 3
= 4 C 0 (1) 4 + 4 C 1 (1) 3
+ 4 C 2 (1) 2
+ 4 C 3 (1)
+ 4 C 4
Ahora, sustituyendo estos valores en la ecuación principal, obtenemos
=
=
=
=
Pregunta 10. Encuentra la expansión de (3x 2 – 2ax + 3a 2 ) 3 usando el teorema del binomio.
Soluciones:
Agrupando (3x 2 – 2ax + 3a 2 ) 3 en forma binomial, tenemos
[3x 2 + (- 2ax + 3a 2 )] 3
Comparándolo con (a+b) n ,
a = 3x 2 , b = -a (2x-3a) y n = 3
[3x 2 + (-a (2x-3a))] 3
= 3 C 0 (3x 2 ) 3 + 3 C 1 (3x 2 ) 2 (-a (2x-3a)) + 3 C 2 (3x 2 ) (-a (2x-3a)) 2 + 3 C 3 ( -a (2x-3a)) 3
= 27x 6 + 3 (9x 4 ) (-a) (2x-3a) + 3 (3x 2 ) (-a) 2 (2x-3a) 2 + (-a) 3 (2x-3a) 3
= 27x 6 + (-54ax 5 + 81a 2 x 4 ) + 9a 2 x 2 (2x-3a) 2 – a 3 (2x-3a) 3
Ahora, obtengamos el valor de (2x-3a) 2 y (2x-3a) 3 .
(2x-3a) 2 = (2x) 2 + (3a) 2 – 2(2x)(3a)
(2x-3a) 2 = 4x 2 + 9a 2 -12xa
(2x-3a) 3 = (2x) 3 – (3a) 3 – 3(2x)(3a)(2x-3a)
(2x-3a) 3 = 8x 3 – 27a 3 – 36x 2 a +54xa 2
Ahora, sustituyendo estos valores en la ecuación principal, obtenemos
= 27x 6 – 54ax 5 + 81a 2 x 4 + 9a 2 x 2 (4x 2 + 9a 2 -12xa) – a 3 (8x 3 – 27a 3 – 36x 2 a + 54xa 2 )
= 27x 6 – 54ax 5 + 81a 2 x 4 + 36a 2 x 4 + 81a 4 x 2 -108x 3 a 3 – (8a 3 x 3 – 27a 6 – 36x 2 a 4 + 54xa 5)
= 27x 6 – 54ax 5 + 117a 2 x 4 + 81a 4 x 2 -108x 3 a 3 – 8a 3 x 3 + 27a 6 + 36x 2 a 4 – 54xa 5
= 27x 6 – 54ax 5 + 117a 2 x 4 – 116a 3 x 3 + 117a 4 x 2 – 54a 5 x + 27a 6
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
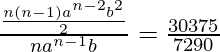
![Rendered by QuickLaTeX.com \times \frac{(\frac{1}{\sqrt[4]{3}})^n}{(\frac{1}{\sqrt[4]{3}})^4} \times (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e604390cf60c8e8b1352eeb9fd6fde7_l3.png)
![Rendered by QuickLaTeX.com \frac{(\frac{1}{\sqrt[4]{3}})^n}{(\frac{1}{3})} (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06e67170f950a7a259d429c553840d13_l3.png)
![Rendered by QuickLaTeX.com \frac{^nC_4 (\frac{(\sqrt[4]{2})^n}{6})}{^nC_4 (\frac{6}{(\sqrt[4]{3})^n})} = \sqrt{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-27ba88ecd6c8511eb782a6e436e3e60d_l3.png)
