Clase 11 Soluciones NCERT – Capítulo 9 Secuencias y series – Ejercicio misceláneo en el Capítulo 9 | Serie 1

Posted on by Rudeus Greyrat

Pregunta 1. Muestre que la suma de (m + n) th y (m – n) th términos de un AP es igual al doble del m th término.

Solución:

Sean a y d el primer término y la diferencia común del AP respectivamente.

(m+n) el término del AP = a+(m+n−1) d

(m−n) el término del PA = a+(m−n−1)  d

Por lo tanto, LHS = a+(m+n−1)d + a+(m−n−1)d 

= 2a+(m+n−1+m−n−1)d

= 2a+(2m−2)d

= 2[a+(m−1)d] = 2a metro  

= lado derecho

Por lo tanto, probado.

Pregunta 2. Si la suma de tres números en AP es 24 y su producto es 440, encuentra los números.

Solución:

Sean tres números a − d, a, a + d.

Suma de estos números = 24

=> a−d+a+a+d = 24

=> 3a = 24

=> un = 8

Producto de estos números = 440

=> (a−d) a (a+d) = 440

=> (8−d) 8 (8+d) = 440

=> 64−d 2 = 55

=> re 2 = 9

=> re = ±3

Cuando a=8, d=3, los números son 

8−3, 8, 8+3, es decir, 5, 8, 11

Cuando a=8, d=−3, los números son

8+3, 8, 8-3, es decir, 11, 8, 5

Pregunta 3. Sea la suma de n, 2n, 3n términos de un AP S 1 , S 2 y S 3 , respectivamente, muestre que S 3 = 3 (S 2 – S 1 ). 

Solución: 

Según la pregunta,

S 1 = Suma de n términos =n[2a+(n−1)d]/2

S 2 = Suma de 2n términos = 2n[2a+(2n−1)d]/2

S 3 = Suma de 3n términos = 3n[2a+(3n−1)d]/2 

Por lo tanto, RHS= 3(S 2 −S 1 ) 

= 3\left[\frac{2n}{2}(2a+(2n−1)d)−\frac{n}{2}(2a+(n−1)d)\right]

=  \frac{3n}{2}[4a+(4n−2)d−2a−(n−1)d]

=  \frac{3n}{2}[4a−2a+(4n−2−n+1)d]

=  \frac{3n}{2}[2a+(3n−1)d]

= S 3 = LHS

Por lo tanto, probado.

Pregunta 4. Encuentra la suma de todos los números entre 200 y 400 que son divisibles por 7.

Solución: 

Los números entre 200 y 400 divisibles por 7 forman un PA con diferencia común (d)=7 y primer término (a)=203.

El último término de esta serie será, a n = 399

También sabemos, a n = a+(n−1)d

=> 399 = 203+(n−1)7

=> (n–1)7 = 196

=> n−1 = 28

=> norte = 29

Suma de la serie =  \frac{n}{2}(a + a n )

=  \frac{29}{2}(203+399) = 8729

Por lo tanto, la suma requerida es 8729.

Pregunta 5. Encuentra la suma de los números enteros del 1 al 100 que son divisibles por 2 o 5.

Solución: 

Sea S 1 la suma de los números enteros del 1 al 100 divisible por 2.

Para S 1, diferencia común (d) = 2 y primer término (a) = 2

El último término será, a n = 100. Por lo tanto,

=> 100 = 2+(n–1)2

=> norte = 50

Por lo tanto, S 1 =  \frac{n}{2}(a + a n )

 =  \frac{50}{2}[2+100] = 2550 

Sea S 2 la suma de los números enteros del 1 al 100 divisible por 5.

Para S 2, Diferencia común(d)=5 y primer término(a)=5

El último término será, a n = 100

=> 100 = 5+(n–1)5

=> norte = 20

Por lo tanto, S 2 =  \frac{20}{2}[5+100] = 1050

Sea S 3 la suma de los números enteros del 1 al 100 divisible por 2 y 5.

Para S 3 , diferencia común (d) = 10 y primer término (a) = 10

El último término será, a n = 100

=> 100 = 10+(n–1)10

=> norte = 10

Por lo tanto, S 3 =  \frac{10}{2}[10+100] = 550

Suma requerida = S 1 + S 2 – S 3

= 2550 + 1050 – 550 

= 3050

Pregunta 6. Encuentra la suma de todos los números de dos dígitos que, cuando se dividen por 4, dan como resto 1.

Solución: 

Los números de dos dígitos, que cuando se dividen por 4, dan 1 como resto son:

13, 17, 21… 97.

Esta serie forma un AP con primer término (a) = 13 y diferencia común (d) = 4.

Sea n el número de términos del AP

Sabemos que el enésimo término de un AP es, a n = a+(n –1 )d

=> 97 = 13 + (n–1)4

=> 4(n–1) = 84

=> norte = 22

Ahora, la suma de n términos de un AP está dada por,

S norte =  \frac{n}{2}[un + un norte ]

=  \frac{22}{2}[13+97] = 1210

Por lo tanto, la suma requerida es 1210.

Pregunta 7. Si f es una función que satisface f(x + y) = f(x) f(y) para todo x, y ∈ N tal que, f(1) = 3 y 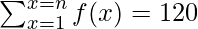 \sum_{x=1}^{x=n} f(x) = 120, encuentra el valor de n.

Solución:

Se nos da eso,

f(x + y) = f(x) × f(y) para todo x, y ∈ N … (1)

f(1) = 3

Poniendo x = y = 1 en (1), tenemos

f(1 + 1) = f(2) = f(1) f(1) = 3 × 3 = 9

Similarmente,

f(1+1+1) = f(3) = f(1+2) = f(1) f(2) = 3 × 9 = 27

Y, f(4) = f(1+3) = f(1) f(3) = 3 × 27 = 81

Tenemos, f(1), f(2), f(3).., es decir, 3, 9, 27, …, 

Esta serie forma un GP con el primer término (a) = 3 y razón común (r) = 3.

Sabemos que la suma de términos en GP está dada por,

S norte = \frac{a(r^n -1)}{r-1}

Y además se da que la suma de términos de la función es 120.

=> 120 = \frac{3(3^n-1)}{3-1}

=> 3n – 1= 80 

=> n=4

Por lo tanto, el número de términos es 4.

Pregunta 8. La suma de algunos términos de GP es 315 cuyo primer término y la razón común son 5 y 2, respectivamente. Encuentra el último término y el número de términos.

Solución:

Sea n el número total de términos.

Sabemos que, la suma de los términos de un GP es,

S norte = \frac{a(r^n -1)}{r-1}

Además, sabemos que el primer término (a) es 5 y la razón común (r) es 2.

=> 315 = \frac{5(2^n-1)}{2-1}

=> 2 n –1 = 63

=> n=6

El último término del GP = 6to término = ar 6-1 = (5)(2) 5 = 160

Por lo tanto, el último término del GP es 160 y el número de términos es 6.  

Pregunta 9. El primer término de un GP es 1. La suma del tercer término y el quinto término es 90. Encuentra la razón común de GP

Solución:

Deje que el primer término y la razón común del GP sean a y r respectivamente.

Tenemos, a = 1. Entonces,

un 3 = ar 2 = r 2  …. (1)

un 5 = un 4= r 4 .. …. (2)

De acuerdo con la pregunta, tenemos

un 3 + un 5 = 90

De (1) y (2),

r2 + r4 = 90

r 4 + r 2 – 9 0 = 0

Resolviendo para r 2 , obtenemos,

r^2 = \frac{-1+\sqrt{(1+360)}}{2} = \frac{-1±19}{2}

r2 = – 10 o r2 = 9

Tomando solo raíces reales, obtenemos,

r = ±3

Por lo tanto, la razón común del GP es ±3.

Pregunta 10. La suma de tres números en GP es 56. Si a estos números les restamos 1, 7, 21 en ese orden, obtenemos una progresión aritmética. Encuentra los números.

Solución:

Suponga que los tres números en GP son a, ar y ar 2 .

Según la pregunta, tenemos

=> a + ar + ar 2 = 56

=> una (1 + r + r 2 )= 56

=> un =  \frac{56}{(1+r+r^2)}  …. (1)

Además, se nos da que,

a – 1, ar – 7, ar 2 – 21 forma un AP 

lo que implica,

=> (ar – 7) – (a – 1) = (ar 2 – 21) – (ar – 7)

=> ar – a – 6 = ar 2 – ar – 14

=> ar 2 – 2ar + a = 8

=> un (r – 1) 2 = 8 ….. (2)

Poniendo el valor de a de (1) en (2), obtenemos,

=>  \frac{56}{(1+r+r^2)}(r – 1) 2 = 8

=> 7(r 2 – 2r + 1) = 1 + r + r 2

=> 6r 2 – 15r + 6 = 0

=> (6r – 3) (r – 2) = 0

=> r = 2, 1/2

Ahora bien, si r = 2, entonces a = 8 y los tres números en GP son 8, 16 y 32.

Si r = 1/2, entonces a = 32 y los tres números en GP son 32, 16 y 8.

Por lo tanto, en ambos casos, los tres números son 8, 16 y 32.  

Pregunta 11. Un GP consta de un número par de términos. Si la suma de todos los términos es 5 veces la suma de los términos que ocupan lugares impares, encuentra su razón común.

Solución: 

Supongamos que los términos en el GP son un 1, un 2 , un 3 , un 4 , … un 2n .

Número de términos = 2n

De acuerdo con la pregunta, tenemos

=> un 1 + un 2 + un 3 + …+ un 2n = 5 [un 1 + un 3 + … + un 2n–1 ]

=> un 1 + un 2 + un 3 + … + un 2n – 5 [un 1 + un 3 + … + un 2n–1 ] = 0

=> un 2 + un 4 + … + un 2n = 4 [un 1 + un 3 + … + un 2n – 1 ]      …. (1)

Ahora, sean los términos de nuestro GP a, ar, ar 2 , ar 3 , …..

Usando la suma de los términos de un GP, ​​la ecuación (1) se convierte en,

\frac{ar(r^n-1)}{r-1} = \frac{4a(r^n-1)}{r-1}

Después de resolver obtenemos,

ar = 4a

r = 4

Por lo tanto, la razón común del GP es 4.

Pregunta 12. La suma de los primeros cuatro términos de un AP es 56. La suma de los últimos cuatro términos es 112. Si su primer término es 11, entonces encuentra el número de términos.

Solución:

Suponga que los términos en AP son a, a + d, a + 2d, a + 3d, … a + (n – 2) d, a + (n – 1)d.

De acuerdo con la pregunta, tenemos,

un = 11,

Suma de los cuatro primeros términos = a + (a + d) + (a + 2d) + (a + 3d) = 4a + 6d,

Suma de los últimos cuatro términos = [a + (n – 4) d] + [a + (n – 3) d] + [a + (n – 2) d] + [a + n – 1) d]

= 4a + (4n – 10) d

Entonces, de acuerdo con la condición dada,

=> 4a + 6d = 56

=> 4(11) + 6d = 56

=> re = 2

Por lo tanto, 4a + (4n –10)d = 112

=> 4(11) + (4n – 10)2 = 112

=> (4n – 10)2 = 68

=> 4n = 44

=> norte = 11

Por tanto, el número de términos del AP es 11.

Pregunta 13. Si, 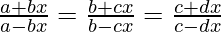 \frac{a+bx}{a-bx} = \frac{b+cx}{b-cx} = \frac{c+dx}{c-dx} , entonces demuestre que a, b, c y d están en GP

Solución:

Se nos da,

\frac{a+bx}{a-bx} = \frac{b+cx}{b-cx}

En la multiplicación cruzada, tenemos,

=> (a+bx)(b-cx) = (b+cx)(a-bx)

=> ab–acx+b 2 x–bcx 2 = ab–b 2 x+acx–bcx 2

=> 2b 2x = 2acx

=> b 2 = ac

=> b/a = c/b ….. (1)

También se nos da,

\frac{b+cx}{b-cx} = \frac{c+dx}{c-dx}

En la multiplicación cruzada, tenemos,

=> (b+cx)(c − dx) = (c+dx)(b − cx)

=> bc − bdx+c 2 x-cdx 2 = bc+bdx − c 2 x − cdx 2

=> 2c 2x = 2bdx

=> c 2 = bd

=> c/d = d/c ….. (2)

De (1) y (2), obtenemos

b/a = c/b = d/c

Por lo tanto, a, b, c y d están en GP

Pregunta 14. Sea S la suma, P el producto y R la suma de los recíprocos de n términos en un GP Demuestre que P 2 R n = S n .

Solución:

Supongamos que los términos en el GP son a, ar, ar 2 , ar 3 , … ar n – 1 …

De acuerdo con la pregunta, tenemos,

S = a(r norte − 1)/(r − 1) ….. (1)

PAG = un norte × r 1 +2+….+n-1

= un n r n(n-1)/2

R = 1/a + 1/ar + 1/ar 2 + …. + 1/ar n-1

= \left(\frac{ r^{n−1}}{r-1}\right) [Tex]\left(\frac{1}{ar^{n-1}}\right)[/Tex]

Entonces, P 2 R n = a 2n r n(n-1) = \frac{(r^n-1)^{n}}{a^nr^{n(n-1)}(r-1)^n}

= \frac{a^n(r^n-1)^n}{(r-1)^n}

= \left[\frac{a(r^n-1)}{r-1}\right]^{n}

De (1), obtenemos,

PAGS 2 R norte = S norte

Por lo tanto, demostrado

Pregunta 15. Los términos p th , q th y r th de un AP son a, b, c respectivamente. Demuestra que (q – r) a + (r – p) b + (p – q) c = 0.

Solución: 

Tomemos t y d como el primer término y la diferencia común de la AP respectivamente.

El n -ésimo término del AP viene dado por, a n = t + (n – 1) d

Por lo tanto,

p el término será, a p = t+ (p – 1) d = a ….. (1)

q el término será, a q = t + ( q – 1) d = b ….. (2)

El r ésimo término será, a r = t + (r – 1) d = c ….. (3)

Al restar la ecuación (2) de (1), obtenemos

=> (p – 1 – q + 1) d = a – b

=> (p – q) d = a – b

=> d =  \frac{a-b}{p-q}  ….. (4)

Al restar la ecuación (3) de (2), obtenemos

=> (q – 1 – r + 1) re = segundo – c

=> (q – r) re = segundo – c

=> re =  \frac{b-c}{q-r}  .…. (5)

Igualando los valores de d obtenidos en (4) y (5), obtenemos

=>  \frac{a-b}{p-q}  = \frac{b-c}{q-r}

=> (a – b)(q – r) = (b – c)(p – q)

=> pb – cp+cq – aq+ar – br = 0

Reordenando términos, obtenemos,

=> ( – aq+ar)+(pb – br)+( – cp+cq) = 0  

=> a(q – r)+b(r – p)+c(p – q) = 0

Por lo tanto, demostrado

Pregunta 16. Si a(1/b+1/c), b(1/c+1/a), c(1/a+1/b) están en AP, prueba que a, b, c están en AP 

Solución:

Nos dan, a(1/b+1/c), b(1/c+1/a), c(1/a+1/b) están en AP

=> b(1/c+1/a)–a(1/b+1/c) = c(1/a+1/b)–b(1/c+1/a)

=> \frac{b(a+c)}{ac}-\frac{a(b+c)}{bc} = \frac{c(a+b)}{ab}-\frac{b(c+a)}{ac}

Multiplicando ambos lados por abc y reorganizando, obtenemos,

=> segundo 2 a–a 2 b +b 2 c–a 2 c  = c 2 a – segundo 2 a+c 2 segundo – segundo 2 c

=> ab(b–a)+c(b 2 –a 2 ) = a(c 2 – b 2 )+bc(c – b)

=> (b – a)(ab+bc+ca) = (c – b)(ab+bc+ca)

=> segundo – un = do – segundo

Por lo tanto, a, b y c están en AP

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *