Prerrequisitos: funciones generadoras , números de Fibonacci , métodos para encontrar números de Fibonacci .
El método de usar Funciones Generadoras para resolver la famosa y útil recurrencia de los Números de Fibonacci ha sido discutido en esta publicación.
La función generadora es una poderosa herramienta para resolver una amplia variedad de problemas matemáticos, incluidos los problemas de conteo. Es una serie de potencias formal. Por ejemplo, en los problemas de conteo, a menudo nos interesa encontrar la cantidad de objetos de tamaño ![]() . En tal caso, definimos una serie de potencias que, en términos simples, es un polinomio de términos infinitos donde el coeficiente del término de
. En tal caso, definimos una serie de potencias que, en términos simples, es un polinomio de términos infinitos donde el coeficiente del término de ![]() grado es el
grado es el ![]() término de la secuencia. Esto nos ayuda a encontrar muchos resultados interesantes e importantes. Cabe señalar que en el uso de funciones generadoras, generalmente usamos los coeficientes en la serie de potencia de la función generadora, rara vez usamos la variable en la serie. En este post también haremos lo mismo. La función generadora ordinaria de algún a n es:
término de la secuencia. Esto nos ayuda a encontrar muchos resultados interesantes e importantes. Cabe señalar que en el uso de funciones generadoras, generalmente usamos los coeficientes en la serie de potencia de la función generadora, rara vez usamos la variable en la serie. En este post también haremos lo mismo. La función generadora ordinaria de algún a n es:
Los números de Fibonacci son una de las sucesiones fundamentales en matemáticas y se han descubierto numerosas formas de encontrar los términos de orden superior de esta sucesión. Esta publicación analiza uno de esos métodos.
Primero definamos una función generadora para los Números de Fibonacci, y luego la función se simplificará para obtener una recurrencia. Usando esto, expanda la simplificación y divídala en fracciones parciales, y luego use dos series de potencia estándar, y luego combínelas para llegar a un resultado sorprendente para el ![]() término de la serie de Fibonacci.
término de la serie de Fibonacci.
Definamos la función generadora ![]() como
como
,
donde
es el iésimo número de Fibonacci.
Ya que,
![]() .
.
![]() .
.
Reorganizándolos obtenemos,
![]() .
.
Tomando los términos comunes,
![]()
![]()
Simplificándolo aún más, se obtiene la siguiente función.
![]() .
.
Resolviendo para ![]() , obtenemos:
, obtenemos:
![]() .
.
Obtenemos la siguiente fórmula por las operaciones anteriores:
,
donde,
y
.
De este modo,
![]()
Also note that,
![]() .
.
Así, manteniendo esta relación en la expresión anterior, obtenemos,
![]() .
.
Ahora, el lado derecho de la expresión anterior se puede separar en fracciones parciales,
![Rendered by QuickLaTeX.com \mathcal{F}(z) = \frac{1}{\sqrt{5}}\left [ \frac{1}{(1-\phi z)} - \frac{1}{(1-\widehat{\phi} z)}\right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-399ddde8c421a3f0766584f1a31b9c05_l3.png) .
.
Usando Expansión en las dos fracciones,
![]() .
.
Similarmente,
![]() .
.
De este modo,
![]() .
.
De este modo,
![]() .
.
Ahora,
![]() ,
,
y,
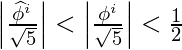
Usando los dos hechos anteriores, se puede concluir con seguridad que el valor de
, redondeado al entero más próximo.
Encontrar el n-ésimo número de Fibonacci usando la proporción áurea es una de las aplicaciones de esta fórmula.
Publicación traducida automáticamente
Artículo escrito por AayushChaturvedi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA