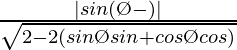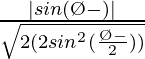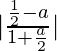Soluciones NCERT Clase 11 – Capítulo 10 Líneas rectas – Ejercicio misceláneo en el Capítulo 10

Pregunta 1. Encuentra los valores de k para los cuales la recta (k – 3)x – (4 – k ² )y + k ² – 7k + 6 = 0 es

(a) Paralelo al eje x

(b) Paralelo al eje y

(c) Pasando por el origen.

Solución:

Nos dan la recta, (k – 3)x – (4 – k ² )y + k ² – 7k + 6 = 0

=> (4 – k ² )y = (k – 3)x + k ² – 7k + 6

=> y = $\frac{(k-3)x}{4-k^2}$ + $\frac{k^2-7k+6}{4-x^2}$

Ahora la ecuación de la línea es de la forma y = mx + c donde m es la pendiente de la línea y c es su intersección con el eje y.

Entonces, obtenemos m = $\frac{k-3}{4-k^2}$ y c = $\frac{k^2-7k+6}{4-x^2}$

(a) Paralelo al eje x

Si la recta es paralela al eje x, entonces tenemos,

Pendiente de la línea = Pendiente del eje x

=> metro = 0

=> $\frac{k-3}{4-k^2}$ = 0

=> k – 3 = 0

=> k = 3

Por lo tanto, si la línea dada es paralela al eje x, entonces el valor de k es 3.

(b) Paralelo al eje y

Si la recta es paralela al eje y, entonces tenemos,

Pendiente de la línea = Pendiente del eje y

=> m = ∞ (indefinido)

=> $\frac{k-3}{4-k^2}$ = ∞

=> k ² − 4 = 0

=> k ² = 4

=> k = ±2

Por lo tanto, si la recta dada es paralela al eje y, entonces el valor de k es ± 2.

(c) Pasando por el origen.

Si la recta pasa por el origen,

Intersección Y = 0

=> c = 0

=> k ² – 7k + 6 = 0

=> (k – 6) (k – 1) = 0

=> k = 1 o k = 6

Por lo tanto, si la línea dada pasa por el origen, entonces el valor de k es 1 o 6.

Pregunta 2. Encuentra los valores de θ y p, si la ecuación x cos θ + y sen θ = p es la forma normal de la recta √3x + y + 2 = 0.

Solución:

Nos dan la línea, √3x + y + 2 = 0.

=> −√3x − y = 2

Al convertir esto a su forma normal, obtenemos

=> $\frac{-\sqrt{3}x}{\sqrt{(-\sqrt{3})^2+(-1)^2}}-\frac{y}{\sqrt{(-\sqrt{3})^2+(-1)^2}}=\frac{2}{\sqrt{(-\sqrt{3})^2+(-1)^2}}$

=> $\frac{-\sqrt{3}x}{2}-\frac{y}{2}=\frac{2}{2}$

=> $\frac{-\sqrt{3}x}{2}-\frac{y}{2}=1$

Al comparar esta ecuación con la forma normal dada x cos θ + y sin θ = p, obtenemos

=> cos θ = $\frac{-\sqrt{3}}{2}$ , sen θ = $\frac{-1}{2}$ y p = 1

Los valores de sen θ y cos θ son negativos. Entonces, θ = π + $\frac{π}{6}$ = $\frac{7π}{6}$ .

Por lo tanto, el valor de θ es $\frac{7π}{6}$ y p es 1.

Pregunta 3. Encuentra las ecuaciones de las líneas, que cortan las intersecciones en los ejes cuya suma y producto son 1 y –6, respectivamente.

Solución:

Supongamos que las intersecciones cortadas por las líneas dadas en los ejes son a y b. De acuerdo con la pregunta, tenemos,

=> un + segundo = 1 . . . . (1)

=> ab = – 6 . . . . (2)

Resolviendo ambas ecuaciones obtenemos

a = 3 y b = –2 o a = –2 y b = 3

Sabemos que la ecuación de la recta cuyas intersecciones son los ejes a y b es,

bx + ay – ab = 0

Cuando a = 3 y b = –2

Entonces la ecuación de la línea es – 2x + 3y + 6 = 0, es decir, 2x – 3y = 6.

Cuando a = –2 y b = 3

Entonces la ecuación de la recta es 3x – 2y + 6 = 0, es decir –3x + 2y = 6.

Por lo tanto, la ecuación requerida de las rectas es 2x – 3y = 6 y –3x + 2y = 6.

Pregunta 4. ¿Cuáles son los puntos en el eje y cuya distancia desde la línea x/3 + y/4 = 1 es de 4 unidades?

Solución:

Supongamos que (0, b) es el punto en el eje y cuya distancia desde la línea x/3 + y/4 = 1 es de 4 unidades.

La línea se puede escribir como 4x + 3y – 12 = 0

Al comparar nuestra ecuación con la ecuación general de la línea Ax + By + C = 0, obtenemos

A = 4, B = 3 y C = –12

Ahora, sabemos que la distancia perpendicular (d) de una línea Ax + By + C = 0 desde (x ₁ , y ₁ ) está dada por,

re = $\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$

Nos dan d = 4. Para el punto (0, b), el valor de d se convierte en,

=> $\frac{|4(0)+3b-12|}{\sqrt{3^2+4^2}}$ = 4

=> $\frac{|3b-12|}{5}$ = 4

=> |3b – 12| = 20

=> 3b – 12 = 20 o 3b – 12 = –20

=> b = 32/3 o b = –8/3

Por lo tanto, (0, 32/3) y (0, –8/3) son los puntos en el eje y cuya distancia a la recta x/3 + y/4 = 1 es de 4 unidades.

Pregunta 5. Encuentra la distancia perpendicular desde el origen hasta la línea que une los puntos (cos θ, sen θ) y (cos Ø, sen Ø).

Solución:

La ecuación de la recta que une los puntos (cos θ, sen θ) y (cos Ø, sen Ø) viene dada por,

=> y – sen θ = $\frac{sin Ø-sin θ}{cos Ø-cos θ}$ (x – cosθ)

=> y(cos Ø – cos θ) – sen θ(cos Ø – cos θ) = x(sen Ø – sen θ) – cos θ(sen Ø – sen θ)

=> x(sen Ø – sen θ) + y(cos Ø – cos θ) + cos θ sen Ø – sen θ cos θ – sen θ cos Ø + sen θ cos θ = 0

=> x(sen Ø – sen θ) + y(cos Ø – cos θ) + sen (Ø – θ) = 0

Entonces, obtenemos, A = sin Ø – sin θ, B = cos Ø – cos θ y C = sin (Ø – θ).

Ahora, sabemos que la distancia perpendicular (d) de una línea Ax + By + C = 0 desde el origen (0, 0) está dada por,

re = $\frac{|C|}{\sqrt{A^2+B^2}}$

= $\frac{|sin(Ø - θ)|}{\sqrt{(sinØ-sinθ)^2+(cosØ-cosθ)^2}}$

= $\frac{|sin(Ø - θ)|}{\sqrt{sin^2Ø+sin^2θ-2sinØsinθ+cos^2Ø+cos^2θ-2cosØcosθ}}$

= $\frac{|sin(Ø - θ)|}{\sqrt{2-2(sinØsinθ+cosØcosθ)}}$

= $\frac{|sin(Ø - θ)|}{\sqrt{2(1-cos(Ø-θ))}}$

= $\frac{|sin(Ø - θ)|}{\sqrt{2(2sin^2(\frac{Ø-θ}{2}))}}$

= $\frac{|sin(Ø - θ)|}{|2sin(\frac{Ø-θ}{2})|}$

Por tanto, $\frac{|sin(Ø - θ)|}{|2sin(\frac{Ø-θ}{2})|}$ es la distancia perpendicular desde el origen hasta la recta dada.

Pregunta 6. Encuentra la ecuación de la línea paralela al eje y y trazada a través del punto de intersección de las líneas x – 7y + 5 = 0 y 3x + y = 0.

Solución:

Dos líneas dadas son

x – 7y + 5 = 0 . . . . (1)

3x + y = 0 . . . . (2)

Resolviendo las ecuaciones (1) y (2) obtenemos

x = −5/22 y y = 15/22

(−5/ 22, 15/22) es el punto de intersección de las rectas (2) y (3)

Ahora la ecuación de cualquier línea paralela al eje y es de la forma

x = un . . . . (1)

Si la recta x = a pasa por el punto (−5/22, 15/22) obtenemos a = −5/22.

Por lo tanto, la ecuación requerida de la recta es x = −5/22.

Pregunta 7. Encuentra la ecuación de una línea trazada perpendicularmente a la línea x/4 + y/6 = 1 a través del punto donde se encuentra con el eje y.

Solución:

La línea dada es, x/4 + y/6 = 1.

=> 3x + 2y – 12 = 0

=> y = −3/2 x + 6, que es de la forma y = mx + c

Aquí la pendiente de la recta dada = −3/2

Entonces la pendiente de la línea perpendicular a la línea dada = −1/(−3/2) = 2/3

Supongamos que la línea dada se cruza con el eje y en (0, y). Entonces, la ecuación de la línea dada se convierte en,

=> y/6 = 1

=> y = 6

Por lo tanto, la recta dada interseca al eje y en (0, 6). Sabemos que la ecuación de la recta que tiene pendiente 2/3 y pasa por el punto (0, 6) está dada por,

=> (y – 6) = 2/3 (x – 0)

=> 3y – 18 = 2x

=> 2x – 3y + 18 = 0

Por lo tanto, la ecuación requerida de la recta es 2x – 3y + 18 = 0.

Pregunta 8. Encuentra el área del triángulo formado por las rectas y – x = 0, x + y = 0 y x – k = 0.

Solución:

se da que

y – x = 0 . . . . (1)

x + y = 0 . . . . (2)

x – k = 0 . . . . (3)

Aquí el punto de intersección de las rectas (1) y (2) es x = 0 e y = 0.

Y el punto de intersección de las rectas (2) y (3) es x = k y y = – k, las rectas (3) y (1) son x = k y y = k.

Entonces los vértices del triángulo formado por las tres rectas dadas son (0, 0), (k, –k) y (k, k).

Aquí el área del triángulo cuyos vértices son (x ₁ , y ₁ ), (x ₂ , y ₂ ) y (x ₃ , y ₃ ) es

un = $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$

= $\frac{1}{2}|0 (-k - k) + k (k - 0) + k (0 + k)|$

= $\frac{1}{2}|k^2+k^2|$

= $\frac{1}{2}|2k^2|$

= k ² unidades cuadradas

Por lo tanto, k ² unidades cuadradas es el área del triángulo formado por las líneas dadas.

Pregunta 9. Encuentra el valor de p para que las tres líneas 3x + y – 2 = 0, px + 2y – 3 = 0 y 2x – y – 3 = 0 puedan intersecarse en un punto.

Solución:

se da que

3x + y – 2 = 0 . . . . (1)

píxeles + 2y – 3 = 0 . . . . (2)

2x – y – 3 = 0 . . . . (3)

Resolviendo las ecuaciones (1) y (3) obtenemos

x = 1 y y = –1

Se da que las tres rectas se cortan en un punto y el punto de intersección de las rectas (1) y (3) también satisfará a la recta (2).

=> p (1) + 2 (–1) – 3 = 0

=> p – 2 – 3 = 0

=> p = 5

Por lo tanto, el valor de p es 5.

Pregunta 10. Si tres líneas cuyas ecuaciones son y = m ₁ x + c ₁ , y = m ₂ x + c ₂ y y = m ₃ x + c ₃ son concurrentes, entonces demuestre que m ₁ (c ₂ – c ₃ ) + metro ₂ (do ₃ – do ₁ ) + metro ₃ (do ₁ – do ₂ ) = 0.

Solución:

se da que

y = metro ₁ X + C ₁ . . . . (1)

y = metro ₂ X + C ₂ . . . . (2)

y = metro ₃ X + C ₃ . . . . (3)

Al restar la ecuación (1) de (2), obtenemos,

=> 0 = (m ₂ – m ₁ ) x + (c ₂ – c ₁ )

=> (m ₁ – m ₂ ) x = do ₂ – do ₁

=> x = $\frac{c_2-c_1}{m_1-m_2}$

Y y = $\frac{m_1(c_2-c_1)}{m_1-m_2}$ + c ₁

=> y = $\frac{m_1c_2-m_1c_1+m_1c_1-m_2c_1}{m_1-m_2}$

=> y = $\frac{m_1c_2-m_2c_1}{m_1-m_2}$

Por lo tanto, ( $\frac{c_2-c_1}{m_1-m_2}$ , $\frac{m_1c_2-m_2c_1}{m_1-m_2}$ ) es el punto de intersección de las rectas (1) y (2).

Como las tres líneas dadas son concurrentes, este punto debe satisfacer la ecuación (3).

=> $\frac{m_1c_2-m_2c_1}{m_1-m_2}=\frac{m_3(c_2-c_1)}{m_1-m_2}+c_3$

=> $\frac{m_1c_2-m_2c_1}{m_1-m_2}=\frac{m_3c_2-m_3c_1+m_1c_3-m_2c_3}{m_1-m_2}$

=> $m_1c_2-m_2c_1-m_3c_2+m_3c_1-m_1c_3+m_2c_3=0$

=> metro ₁ (do ₂ – do ₃ ) + metro ₂ (do ₃ – do ₁ ) + metro ₃ (do ₁ – do ₂ ) = 0

Por lo tanto probado.

Pregunta 11. Halla la ecuación de las rectas que pasan por el punto (3, 2) que forma un ángulo de 45° con la recta x – 2y = 3.

Solución:

Supongamos que a es la pendiente de la recta que pasa por el punto (3, 2).

La recta dada es x – 2y = 3.

y = 1/2 x – 3/2 que es de la forma y = mx + c.

Entonces, la pendiente de la línea dada b = 1/2

Sabemos que el ángulo entre la línea requerida y la línea x – 2y = 3 es 45 ^o . El ángulo está dado por,

tan θ = $|\frac{\frac{1}{2}-a}{1+\frac{a}{2}}|$

=> bronceado 45 ⁰ = $|\frac{\frac{1}{2}-a}{1+\frac{a}{2}}|$

=> $|\frac{\frac{1}{2}-a}{1+\frac{a}{2}}|$ = 1

=> $\frac{1-2a}{2+a}=\pm1$

=> 2 + a = 1 – 2a o 2 + a = – 1 + 2a

=> a = –1/3 o a = 3

Cuando a = 3, la ecuación de la recta que pasa por (3, 2) y tiene pendiente 3 es,

=> y-2 = 3 (x-3)

=> y-2 = 3x-9

=> 3x – y = 7

Cuando a = –1/3, la ecuación de la recta que pasa por (3, 2) y tiene pendiente –1/3 es

=> y – 2 = –1/3 (x – 3)

=> 3y – 6 = – x + 3

=> x + 3y = 9

Por tanto, las ecuaciones de las rectas son 3x – y = 7 y x + 3y = 9.

Pregunta 12. Encuentra la ecuación de la línea que pasa por el punto de intersección de las líneas 4x + 7y – 3 = 0 y 2x – 3y + 1 = 0 que tiene intersecciones iguales en los ejes.

Solución:

Suponga que la ecuación de la línea que tiene intersecciones iguales en los ejes como

=> x/a + y/a = 1

=> x + y = un . . . . (1)

Al resolver las ecuaciones 4x + 7y – 3 = 0 y 2x – 3y + 1 = 0, obtenemos,

x = 1/13 y y = 5/13

(1/13, 5/13) es el punto de intersección de dos rectas dadas.

Poniendo (1), obtenemos,

=> un = 1/13 + 5/13

=> un = 6/13

Aquí la ecuación (1) se convierte en

=> x + y = 6/13

=> 13x + 13y = 6

Por lo tanto, la ecuación requerida de la recta es 13x + 13y = 6.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Soluciones NCERT Clase 11 – Capítulo 10 Líneas rectas – Ejercicio misceláneo en el Capítulo 10 | Serie 1

Pregunta 1. Encuentra los valores de k para los cuales la recta (k – 3)x – (4 – k ² )y + k ² – 7k + 6 = 0 es

Pregunta 2. Encuentra los valores de θ y p, si la ecuación x cos θ + y sen θ = p es la forma normal de la recta √3x + y + 2 = 0.

Pregunta 3. Encuentra las ecuaciones de las líneas, que cortan las intersecciones en los ejes cuya suma y producto son 1 y –6, respectivamente.

Pregunta 4. ¿Cuáles son los puntos en el eje y cuya distancia desde la línea x/3 + y/4 = 1 es de 4 unidades?

Pregunta 5. Encuentra la distancia perpendicular desde el origen hasta la línea que une los puntos (cos θ, sen θ) y (cos Ø, sen Ø).

Pregunta 6. Encuentra la ecuación de la línea paralela al eje y y trazada a través del punto de intersección de las líneas x – 7y + 5 = 0 y 3x + y = 0.

Pregunta 7. Encuentra la ecuación de una línea trazada perpendicularmente a la línea x/4 + y/6 = 1 a través del punto donde se encuentra con el eje y.

Pregunta 8. Encuentra el área del triángulo formado por las rectas y – x = 0, x + y = 0 y x – k = 0.

Pregunta 9. Encuentra el valor de p para que las tres líneas 3x + y – 2 = 0, px + 2y – 3 = 0 y 2x – y – 3 = 0 puedan intersecarse en un punto.

Pregunta 10. Si tres líneas cuyas ecuaciones son y = m ₁ x + c ₁ , y = m ₂ x + c ₂ y y = m ₃ x + c ₃ son concurrentes, entonces demuestre que m ₁ (c ₂ – c ₃ ) + metro ₂ (do ₃ – do ₁ ) + metro ₃ (do ₁ – do ₂ ) = 0.

Pregunta 11. Halla la ecuación de las rectas que pasan por el punto (3, 2) que forma un ángulo de 45° con la recta x – 2y = 3.

Pregunta 12. Encuentra la ecuación de la línea que pasa por el punto de intersección de las líneas 4x + 7y – 3 = 0 y 2x – 3y + 1 = 0 que tiene intersecciones iguales en los ejes.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra los valores de k para los cuales la recta (k – 3)x – (4 – k 2 )y + k 2 – 7k + 6 = 0 es

Pregunta 2. Encuentra los valores de θ y p, si la ecuación x cos θ + y sen θ = p es la forma normal de la recta √3x + y + 2 = 0.

Pregunta 3. Encuentra las ecuaciones de las líneas, que cortan las intersecciones en los ejes cuya suma y producto son 1 y –6, respectivamente.

Pregunta 4. ¿Cuáles son los puntos en el eje y cuya distancia desde la línea x/3 + y/4 = 1 es de 4 unidades?

Pregunta 5. Encuentra la distancia perpendicular desde el origen hasta la línea que une los puntos (cos θ, sen θ) y (cos Ø, sen Ø).

Pregunta 6. Encuentra la ecuación de la línea paralela al eje y y trazada a través del punto de intersección de las líneas x – 7y + 5 = 0 y 3x + y = 0.

Pregunta 7. Encuentra la ecuación de una línea trazada perpendicularmente a la línea x/4 + y/6 = 1 a través del punto donde se encuentra con el eje y.

Pregunta 8. Encuentra el área del triángulo formado por las rectas y – x = 0, x + y = 0 y x – k = 0.

Pregunta 9. Encuentra el valor de p para que las tres líneas 3x + y – 2 = 0, px + 2y – 3 = 0 y 2x – y – 3 = 0 puedan intersecarse en un punto.

Pregunta 10. Si tres líneas cuyas ecuaciones son y = m 1 x + c 1 , y = m 2 x + c 2 y y = m 3 x + c 3 son concurrentes, entonces demuestre que m 1 (c 2 – c 3 ) + metro 2 (do 3 – do 1 ) + metro 3 (do 1 – do 2 ) = 0.

Pregunta 11. Halla la ecuación de las rectas que pasan por el punto (3, 2) que forma un ángulo de 45° con la recta x – 2y = 3.

Pregunta 12. Encuentra la ecuación de la línea que pasa por el punto de intersección de las líneas 4x + 7y – 3 = 0 y 2x – 3y + 1 = 0 que tiene intersecciones iguales en los ejes.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra los valores de k para los cuales la recta (k – 3)x – (4 – k ² )y + k ² – 7k + 6 = 0 es

Pregunta 10. Si tres líneas cuyas ecuaciones son y = m ₁ x + c ₁ , y = m ₂ x + c ₂ y y = m ₃ x + c ₃ son concurrentes, entonces demuestre que m ₁ (c ₂ – c ₃ ) + metro ₂ (do ₃ – do ₁ ) + metro ₃ (do ₁ – do ₂ ) = 0.