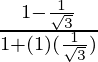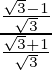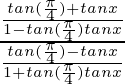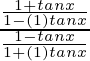Clase 11 Soluciones NCERT – Capítulo 3 Función trigonométrica – Ejercicio 3.3

Pruebalo:

Pregunta 1: sen ²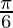 $\frac{\pi}{6}$ + cos ² 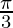$\frac{\pi}{3}$ – tan ² $\frac{\pi}{4}$ = $-\frac{1}{2}$

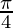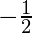
Solución:

Teniendo en cuenta LHS, obtenemos

= sen ² $\frac{\pi}{6}$ + cos ² $\frac{\pi}{3}$ – tan ² $\frac{\pi}{4}$

Sustituyendo los valores,

= $(\frac{1}{2})^2 + (\frac{1}{2})^2 - (1)^2$

= $\frac{1}{2}$ – 1

= $-\frac{1}{2}$

Por lo tanto, LHS = RHS

Pregunta 2: 2sen ²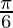 $\frac{\pi}{6}$ + cosec ² 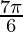$\frac{7\pi}{6}$ cos ² $\frac{\pi}{3}$ = $\frac{3}{2}$

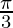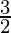
Solución:

Teniendo en cuenta LHS, obtenemos

= 2sen ² $\frac{\pi}{6}$ +coseg ² $(\pi + \frac{\pi}{6})$ cos ² $\frac{\pi}{3}$

= 2sen ² $\frac{\pi}{6}$ + (- cosec $\frac{\pi}{6})^2$ cos ² $\frac{\pi}{3}$

Sustituyendo los valores,

= $2(\frac{1}{2})^2 + ((-2)^2) (\frac{1}{2})^2$

= 2 $(\frac{1}{4})$ + 4 $(\frac{1}{4})$

= $\frac{1}{2}$ + 1

= $\frac{3}{2}$

Por lo tanto, LHS = RHS

Pregunta 3: cot ²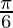 $\frac{\pi}{6}$ + cosec 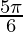$\frac{5\pi}{6}$ + 3tan ² 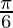$\frac{\pi}{6}$ = 6

Solución:

Teniendo en cuenta LHS, obtenemos

= cot ² $\frac{\pi}{6}$ + cosec $(\pi - \frac{\pi}{6})$ + 3tan ² $\frac{\pi}{6}$

= cot ² $\frac{\pi}{6}$ + cosec $\frac{\pi}{6}$ + 3tan ² $\frac{\pi}{6}$

Sustituyendo los valores,

= (√3) ² + 2 + 3 $(\frac{1}{\sqrt{3}})^2$

= 3 + 2 + 3 $(\frac{1}{3})$

= 6

Por lo tanto, LHS = RHS

Pregunta 4: 2sen ²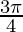 $\frac{3\pi}{4}$ + 2cos ² 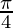$\frac{\pi}{4}$ + 2sec ² 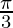$\frac{\pi}{3}$ = 10

Solución:

Teniendo en cuenta LHS, obtenemos

= 2sen ² $(\pi - \frac{\pi}{4})$ + 2cos ² $\frac{\pi}{4}$ + 2seg ² $\frac{\pi}{3}$

= 2sen ² $\frac{\pi}{4}$ + 2cos ² $\frac{\pi}{4}$ + 2seg ² $\frac{\pi}{3}$

Sustituyendo los valores,

= $2(\frac{1}{\sqrt{2}})^2 + 2(\frac{1}{\sqrt{2}})^2 + 2(2)^2$

= 2 $(\frac{1}{2}) + 2(\frac{1}{2})$ + 2(4)

= 1 + 1 + 8

= 10

Por lo tanto, LHS = RHS

Pregunta 5: Encuentra el valor de:

(i) sen 75°

Solución:

Como no conocemos el valor del ángulo de 75°, dividiremos los ángulos que conocemos.

75° = 30° + 45°, entonces usemos esto y resolvamos para sin(30° + 45°)

Usando la fórmula trigonométrica,

sen (A+B) = sen A cos B + cos A sen B

sen(30° + 45°) = sen 30° cos 45° + cos 30° sen 45°

Sustituyendo valores, obtenemos

pecado(75°) = $(\frac{1}{2}) (\frac{1}{\sqrt{2}}) + (\frac{\sqrt{3}}{2}) (\frac{1}{\sqrt{2}})$

pecado(75°) = $(\frac{1}{2\sqrt{2}}) + (\frac{\sqrt{3}}{2\sqrt{2}})$

pecado(75°) = $(\frac{1+\sqrt{3}}{2\sqrt{2}})$

(ii) tan 15°

Solución:

Como no conocemos el valor del ángulo de 15°, dividiremos los ángulos que conocemos.

15° = 60° – 45° o 45° – 30° así que usemos esto y resolvamos para tan(45° – 30°)

Usando la fórmula trigonométrica,

bronceado (AB) = $\mathbf{\frac{tan A-tan B}{1+tan A tan B}}$

tan(45° – 30°) = $\frac{tan 45\degree-tan 30\degree}{1+tan 45\degree tan 30\degree}$

Sustituyendo valores, obtenemos

bronceado(15°) = $\frac{1-\frac{1}{\sqrt{3}}}{1+(1)(\frac{1}{\sqrt{3}})}$

bronceado(15°) = $\frac{\frac{\sqrt{3}-1}{\sqrt{3}}}{\frac{\sqrt{3}+1}{\sqrt{3}}}$

bronceado(15°) = $\frac{\sqrt{3}-1}{\sqrt{3}+1}$

Ahora racionalizando el denominador, multiplica y divide por $(\sqrt{3}-1)$

bronceado(15°) = $\frac{\sqrt{3}-1}{\sqrt{3}+1} \times \frac{\sqrt{3}-1}{\sqrt{3}-1}$

bronceado(15°) = $\frac{(\sqrt{3}-1)^2}{(\sqrt{3})^2-1^2}$

bronceado(15°) = $\frac{(\sqrt{3})^2+1^2 - 2(\sqrt{3})(1)}{3-1}$

bronceado(15°) = $\frac{3+1 - 2\sqrt{3}}{2}$

bronceado(15°) = $\frac{4 - 2\sqrt{3}}{2}$

tan(15°) = 2 – $\sqrt{3}$

Demuestra lo siguiente:

Pregunta 6: 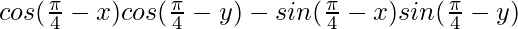$cos (\frac{\pi}{4}-x)cos (\frac{\pi}{4}-y)- sin (\frac{\pi}{4}-x)sin (\frac{\pi}{4}-y)$ = sen (x+y)

Solución:

Teniendo en cuenta LHS, obtenemos

= $cos (\frac{\pi}{4}-x)cos (\frac{\pi}{4}-y)- sin (\frac{\pi}{4}-x)sin (\frac{\pi}{4}-y)$

Como aquí hay una multiplicación de cos cos y sin sin, usaremos las fórmulas de desfactorización,

2 cos A cos B = cos (A+B) + cos (AB) y, ……………….(1)

2 sen A sen B = cos (AB) – cos (A+B) ……………….(2)

Multiplica y divide LHS por 2, obtenemos

= $\frac{2}{2}(cos (\frac{\pi}{4}-x)cos (\frac{\pi}{4}-y)- sin (\frac{\pi}{4}-x)sin (\frac{\pi}{4}-y))$

= $\frac{1}{2}(2 cos (\frac{\pi}{4}-x)cos (\frac{\pi}{4}-y)- 2 sin (\frac{\pi}{4}-x)sin (\frac{\pi}{4}-y))$

Restando (2) de (1) y usando fórmulas de identidad, obtenemos

2 cos A cos B – 2 sen A sen B = cos (A+B) + cos (AB) – (cos (AB) – cos (A+B))

2 cos A cos B – 2 sen A sen B = 2 cos (A+B)

Por lo tanto, usando este

= $\frac{1}{2}[2 cos ((\frac{\pi}{4}-x)+ (\frac{\pi}{4}-y))]$

= porque $(\frac{2\pi}{4}-x-y)$

= porque $(\frac{\pi}{2}-(x+y))$

= sen (x+y) (As cos $(\frac{\pi}{2}-\theta)$ = sen θ)

Por lo tanto, LHS = RHS

Pregunta 7: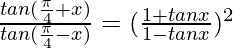 $\frac{tan(\frac{\pi}{4}+x)}{tan(\frac{\pi}{4}-x)} = (\frac{1+tan x}{1-tan x})^2$

Solución:

Teniendo en cuenta LHS, obtenemos

$\frac{tan(\frac{\pi}{4}+x)}{tan(\frac{\pi}{4}-x)}$

Como, usando fórmulas de factorización de tan, tenemos

tan (A+B) = $\mathbf{\frac{tan A + tan B}{1 - tan A tan B}}$ y,

bronceado (AB) = $\mathbf{\frac{tan A - tan B}{1 + tan A tan B}}$

Ahora, reemplazando los valores

= $\frac{\frac{tan (\frac{\pi}{4}) + tan x}{1 - tan (\frac{\pi}{4}) tan x}}{\frac{tan (\frac{\pi}{4}) - tan x}{1 + tan (\frac{\pi}{4}) tan x}}$

= $\frac{\frac{1 + tan x}{1 - (1) tan x}}{\frac{1 - tan x}{1 + (1) tan x}}$

= $\frac{1 + tan x}{1 - tan x} \times \frac{1 + tan x}{1 - tan x}$

= $(\frac{1 + tan x}{1 - tan x})^2$

Por lo tanto, LHS = RHS

Pregunta 8: 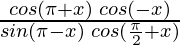$\frac{cos(\pi + x)\hspace{0.1cm}cos(-x)}{sin (\pi-x) \hspace{0.1cm}cos(\frac{\pi}{2}+x)}$ = cuna ² x

Solución:

Teniendo en cuenta LHS, obtenemos

= $\frac{cos(\pi + x)\hspace{0.1cm}cos(-x)}{sin (\pi-x) \hspace{0.1cm}cos(\frac{\pi}{2}+x)}$

Como conocemos estos valores estándar

cos(-x) = cos x

cos $(\pi + x)$ = – cos x

pecado $(\pi-x)$ = pecado x

cos $(\frac{\pi}{2} + x)$ = – sen x

Sustituyendo estos valores, tenemos

= $\frac{(-cos x)\hspace{0.1cm}cos x}{sin x \hspace{0.1cm}(- sin x)}$

= $\frac{cos^2 x}{sin^2 x}$

= cuna ² x

Por lo tanto, LHS = RHS

Pregunta 9: $cos (\frac{3\pi}{2}+x)\hspace{0.1cm}cos (2\pi+x)[\hspace{0.1cm}cot (\frac{3\pi}{2}-x)+cot(2\pi+x)]$ = 1

Solución:

Teniendo en cuenta LHS, obtenemos

= $cos (\frac{3\pi}{2}+x)\hspace{0.1cm}cos (2\pi+x)[\hspace{0.1cm}cot (\frac{3\pi}{2}-x)+cot(2\pi+x)]$

Como conocemos estos valores estándar

cos $(\frac{3\pi}{2}+x)$ = sen x

cos $(2\pi + x)$ = cos x

cuna $(2\pi + x)$ = cuna x

cuna $(\frac{3\pi}{2}-x)$ = bronceado x

Sustituyendo los valores, tenemos

= $sin x\hspace{0.1cm}cos x[\hspace{0.1cm}tan x + cot x]$

= $sin x\hspace{0.1cm}cos x[\frac{sin x}{cos x} + \frac{cos x}{sin x}]$

= $sin x\hspace{0.1cm}cos x[\frac{sin^2 x + cos^2 x}{sin x \hspace{0.1cm}cos x}]$

Como sen ² x + cos ² x = 1

= 1

Por lo tanto, LHS = RHS

Pregunta 10: sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x = cos x

Solución:

Teniendo en cuenta LHS, obtenemos

= sen(n + 1)x sen(n + 2)x + cos(n + 1)x cos(n + 2)x

Como aquí hay una multiplicación de cos cos y sin sin, usaremos las fórmulas de desfactorización,

2 cos A cos B = cos (A+B) + cos (AB) y , ……………….(1)

2 sen A sen B = cos (AB) – cos (A+B) ……………….(2)

Multiplica y divide LHS por 2, obtenemos

= $\frac{2}{2}$ (sen(n + 1)x sen(n + 2)x + cos(n + 1)x cos(n + 2)x)

= $\frac{1}{2}$ (2 sen(n + 1)x sen(n + 2)x + 2 cos(n + 1)x cos(n + 2)x)

Sumando (1) y (2) y usando fórmulas de identidad, obtenemos

2 cos A cos B + 2 sen A sen B = cos (A+B) + cos (AB) + cos (AB) – cos (A+B)

2 cos A cos B + 2 sen A sen B = 2 cos (AB)

Por lo tanto, usando este

= $\frac{1}{2}$ (2 cos((n + 1)x – (n + 2)x))

= cos((n + 1)x – (n + 2)x)

= coseno (x-2x)

= coseno (- x)

= cos x (As, cos(-x) = cos x)

Por lo tanto, LHS = RHS

Pregunta 11: 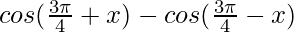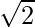$cos (\frac{3\pi}{4}+x)-cos (\frac{3\pi}{4}-x)$ = – $\sqrt{2}$ sen x

Solución:

Teniendo en cuenta LHS, obtenemos

= $cos (\frac{3\pi}{4}+x)-cos (\frac{3\pi}{4}-x)$

Usando la identidad,

cos A – cos B = 2 sen $\mathbf{(\frac{A+B}{2})}$ sen $\mathbf{(\frac{B-A}{2})}$

Sustituyendo los valores,

= $2 sin (\frac{(\frac{3\pi}{4}-x)+(\frac{3\pi}{4}+x)}{2}) sin (\frac{(\frac{3\pi}{4}-x)-(\frac{3\pi}{4}+x)}{2})$

= 2 pecado $(\frac{6\pi}{4\times 2})$ pecado $(\frac{(-x-x)}{2})$

= 2 sen $(\frac{3\pi}{4})$ sen (-x)

= 2 sen $(\pi - \frac{\pi}{4})$ sen (-x)

= 2 ( pecado $(\frac{\pi}{4})$ ) pecado (-x)

= 2 $(\frac{1}{\sqrt{2}})$ (- sen x)

= $\frac{-2 sin x}{\sqrt{2}}$

Racionalizando el denominador, multiplicando y dividiendo por $\sqrt{2}$

= $\frac{-2 sin x}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$

= $\frac{-2 \sqrt{2} \hspace{0.1cm}sin x}{(\sqrt{2})^2}$

= $\frac{-2 \sqrt{2}\hspace{0.1cm} sin x}{2}$

= $-\sqrt{2}$ sen x

Por lo tanto, LHS = RHS

Pregunta 12: sen ² 6x – sen ² 4x = sen 2x sen 10x

Solución:

Teniendo en cuenta LHS, obtenemos

= sen ² 6x – sen ² 4x

= sen 6x sen 6x – sen 4x sen 4x

Como aquí hay multiplicación de sin sin, usaremos fórmulas de desfactorización,

2 sen A sen B = cos (AB) – cos (A+B)

Multiplica y divide LHS por 2, obtenemos

= $\frac{2}{2}$ (sen 6x sen 6x – sen 4x sen 4x)

= $\frac{1}{2}$ (2 sen 6x sen 6x – 2 sen 4x sen 4x)

Usando la identidad, podemos simplificar

= $\frac{1}{2}$ [(cos(6x-6x) – cos(6x+6x)) – (cos(4x-4x) – cos(4x+4x))]

= $\frac{1}{2}$ [(cos(0) – cos(12x)) – (cos(0) – cos(8x))]

= $\frac{1}{2}$ [1 – cos(12x) – 1 + cos(8x)] (As, cos 0 = 1)

= $\frac{1}{2}$ [cos(8x) – cos(12x)]

Ahora, usando la identidad

cos A – cos B = 2 sen $\mathbf{(\frac{A+B}{2})}$ sen $\mathbf{(\frac{B-A}{2})}$

Sustituyendo los valores, tenemos

= $\frac{1}{2}[2 \hspace{0.1cm}sin (\frac{8x+12x}{2}) \hspace{0.1cm}sin (\frac{12x-8x}{2})]$

= pecado $(\frac{20x}{2})$ pecado $(\frac{4x}{2})$

= sen (10 x) sen (2x)

Por lo tanto, LHS = RHS

Pregunta 13: cos ² 2x – cos ² 6x = sen 4x sen 8x

Solución:

Teniendo en cuenta LHS, obtenemos

= cos ² 2x – cos ² 6x

= cos 2x cos 2x – cos 6x cos 6x

Como aquí hay multiplicación de cos cos, usaremos fórmulas de desfactorización,

2 cos A cos B = cos (A+B) + cos (AB)

Multiplica y divide LHS por 2, obtenemos

= $\frac{2}{2}$ (cos 2x cos 2x – cos 6x cos 6x)

= $\frac{1}{2}$ (2 cos 2x cos 2x – 2 cos 6x cos 6x)

Usando la identidad, podemos simplificar

= $\frac{1}{2}$ [(cos(2x+2x) + cos(2x-2x)) – (cos(6x+6x) + cos(6x-6x))]

= $\frac{1}{2}$ [(cos(2x+2x) + cos(0)) – (cos(6x+6x) + cos(0))]

= $\frac{1}{2}$ [(cos(4x) + 1 – cos(12x) – 1)] (As, cos 0 = 1)

= $\frac{1}{2}$ [cos(4x) – cos(12x)]

Ahora, usando la identidad

cos A – cos B = 2 sen $\mathbf{(\frac{A+B}{2})}$ sen $\mathbf{(\frac{B-A}{2})}$

Sustituyendo los valores, tenemos

= $\frac{1}{2}[2 \hspace{0.1cm}sin (\frac{4x+12x}{2}) \hspace{0.1cm}sin (\frac{12x-4x}{2})]$

= pecado $(\frac{16x}{2})$ pecado $(\frac{8x}{2})$

= sen (8x) sen (4x)

Por lo tanto, LHS = RHS

Pregunta 14: sen 2x + 2 sen 4x + sen 6x = 4 cos ² x sen 4x

Solución:

Teniendo en cuenta LHS, obtenemos

sen 2x + 2 sen 4x + sen 6x

Después de reorganizar, tenemos

= (sen 2x + sen 6x) + 2 sen 4x

Usando la identidad, podemos simplificar

sen A+ sen B = 2 sen $\mathbf{(\frac{A+B}{2})}$ cos $\mathbf{(\frac{A-B}{2})}$

= 2 sen $(\frac{6x+2x}{2})$ cos $(\frac{6x-2x}{2})$ + 2 sen 4x

= 2 sen $(\frac{8x}{2})$ cos $(\frac{4x}{2})$ + 2 sen 4x

= 2 sen (4x) cos (2x) + 2 sen 4x

Tomando (2 sen 4x), tenemos

= 2 sen (4x) (cos (2x) + 1)

= 2 sen (4x) (2 cos ² x – 1 + 1) (As, cos 2θ = 2 cos ² θ – 1 )

= 2 sen (4x) (2 cos ² x)

= 4 sen (4x) cos ² x

Por lo tanto, LHS = RHS

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones NCERT – Capítulo 3 Función trigonométrica – Ejercicio 3.3 | Serie 1

Pruebalo:

Pregunta 1: sen ² $\frac{\pi}{6}$ + cos ² $\frac{\pi}{3}$ – tan ² $\frac{\pi}{4}$ = $-\frac{1}{2}$

Pregunta 2: 2sen ² $\frac{\pi}{6}$ + cosec ² $\frac{7\pi}{6}$ cos ² $\frac{\pi}{3}$ = $\frac{3}{2}$

Pregunta 3: cot ² $\frac{\pi}{6}$ + cosec $\frac{5\pi}{6}$ + 3tan ² $\frac{\pi}{6}$ = 6

Pregunta 4: 2sen ² $\frac{3\pi}{4}$ + 2cos ² $\frac{\pi}{4}$ + 2sec ² $\frac{\pi}{3}$ = 10

Pregunta 5: Encuentra el valor de:

(i) sen 75°

(ii) tan 15°

Demuestra lo siguiente:

Pregunta 6: $cos (\frac{\pi}{4}-x)cos (\frac{\pi}{4}-y)- sin (\frac{\pi}{4}-x)sin (\frac{\pi}{4}-y)$ = sen (x+y)

Pregunta 7: $\frac{tan(\frac{\pi}{4}+x)}{tan(\frac{\pi}{4}-x)} = (\frac{1+tan x}{1-tan x})^2$

Pregunta 8: $\frac{cos(\pi + x)\hspace{0.1cm}cos(-x)}{sin (\pi-x) \hspace{0.1cm}cos(\frac{\pi}{2}+x)}$ = cuna ² x

Pregunta 9: $cos (\frac{3\pi}{2}+x)\hspace{0.1cm}cos (2\pi+x)[\hspace{0.1cm}cot (\frac{3\pi}{2}-x)+cot(2\pi+x)]$ = 1

Pregunta 10: sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x = cos x

Pregunta 11: $cos (\frac{3\pi}{4}+x)-cos (\frac{3\pi}{4}-x)$ = – $\sqrt{2}$ sen x

Pregunta 12: sen ² 6x – sen ² 4x = sen 2x sen 10x

Pregunta 13: cos ² 2x – cos ² 6x = sen 4x sen 8x

Pregunta 14: sen 2x + 2 sen 4x + sen 6x = 4 cos ² x sen 4x

Deja una respuesta Cancelar la respuesta

Pruebalo:

Pregunta 1: sen 2 + cos 2 – tan 2 =

Pregunta 2: 2sen 2 + cosec 2 cos 2 =

Pregunta 3: cot 2 + cosec + 3tan 2 = 6

Pregunta 4: 2sen 2 + 2cos 2 + 2sec 2 = 10

Pregunta 5: Encuentra el valor de:

(i) sen 75°

(ii) tan 15°

Demuestra lo siguiente:

Pregunta 6: = sen (x+y)

Pregunta 7:

Pregunta 8: = cuna 2 x

Pregunta 9: = 1

Pregunta 10: sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x = cos x

Pregunta 11: = – sen x

Pregunta 12: sen 2 6x – sen 2 4x = sen 2x sen 10x

Pregunta 13: cos 2 2x – cos 2 6x = sen 4x sen 8x

Pregunta 14: sen 2x + 2 sen 4x + sen 6x = 4 cos 2 x sen 4x

Deja una respuesta Cancelar la respuesta

Pregunta 1: sen ² $\frac{\pi}{6}$ + cos ² $\frac{\pi}{3}$ – tan ² $\frac{\pi}{4}$ = $-\frac{1}{2}$

Pregunta 2: 2sen ² $\frac{\pi}{6}$ + cosec ² $\frac{7\pi}{6}$ cos ² $\frac{\pi}{3}$ = $\frac{3}{2}$

Pregunta 3: cot ² $\frac{\pi}{6}$ + cosec $\frac{5\pi}{6}$ + 3tan ² $\frac{\pi}{6}$ = 6

Pregunta 4: 2sen ² $\frac{3\pi}{4}$ + 2cos ² $\frac{\pi}{4}$ + 2sec ² $\frac{\pi}{3}$ = 10

Pregunta 6: $cos (\frac{\pi}{4}-x)cos (\frac{\pi}{4}-y)- sin (\frac{\pi}{4}-x)sin (\frac{\pi}{4}-y)$ = sen (x+y)

Pregunta 7: $\frac{tan(\frac{\pi}{4}+x)}{tan(\frac{\pi}{4}-x)} = (\frac{1+tan x}{1-tan x})^2$

Pregunta 8: $\frac{cos(\pi + x)\hspace{0.1cm}cos(-x)}{sin (\pi-x) \hspace{0.1cm}cos(\frac{\pi}{2}+x)}$ = cuna ² x

Pregunta 9: $cos (\frac{3\pi}{2}+x)\hspace{0.1cm}cos (2\pi+x)[\hspace{0.1cm}cot (\frac{3\pi}{2}-x)+cot(2\pi+x)]$ = 1

Pregunta 11: $cos (\frac{3\pi}{4}+x)-cos (\frac{3\pi}{4}-x)$ = – $\sqrt{2}$ sen x

Pregunta 12: sen ² 6x – sen ² 4x = sen 2x sen 10x

Pregunta 13: cos ² 2x – cos ² 6x = sen 4x sen 8x

Pregunta 14: sen 2x + 2 sen 4x + sen 6x = 4 cos ² x sen 4x