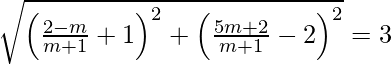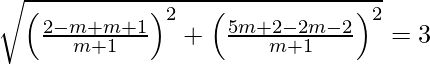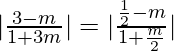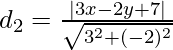Soluciones NCERT Clase 11 – Capítulo 10 Líneas rectas – Ejercicio misceláneo en el Capítulo 10

Pregunta 13. Demuestra que la ecuación de la recta que pasa por el origen y forma un ángulo θ con la recta y = mx + c es 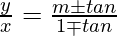$\frac{y}{x}=\frac{m\pm tanθ}{1\mp tanθ}$ .

Solución:

Supongamos que y = m ₁ x es la ecuación de la línea que pasa por el origen. Por lo tanto, la pendiente de esta línea es,

metro ₁ = $\frac{y}{x}$

La recta dada es y = mx + c cuya pendiente es m. Forma un ángulo θ con la línea y = m ₁ x.

=> tan θ = $|\frac{m_1-m}{1+m_1m}|$

=> $|\frac{\frac{y}{x}-m}{1+\frac{mi}{x}}|$ = tan θ

=> $\pm\left(\frac{\frac{y}{x}-m}{1+\frac{my}{x}}\right)$ = tan θ

=> $tanθ+\frac{y}{x}mtanθ=\frac{y}{x}-m$ o $tanθ+\frac{y}{x}mtanθ=-\frac{y}{x}+m$

=> $\frac{y}{x}(1-mtanθ)=m+tanθ$ o $\frac{y}{x}(1+mtanθ)=m-tanθ$

=> $\frac{y}{x}=\frac{m+tanθ}{1-mtanθ}$ o $\frac{y}{x}=\frac{m-tanθ}{1+mtanθ}$

=> $\frac{y}{x}=\frac{m\pm tanθ}{1\mp tanθ}$

Por lo tanto probado.

Pregunta 14. ¿En qué proporción la recta que une (–1, 1) y (5, 7) se divide por la recta x + y = 4?

Solución:

Sabemos que la ecuación de la recta que une (–1, 1) y (5, 7) viene dada por,

=> y – 1 = $\frac{7-1}{5+1}$ (x + 1)

=> y – 1 = x + 1

=> x – y + 2 = 0 . . . . (1)

Nos dan la línea, x + y = 4 . . . . (2)

Resolviendo (1) y (2), obtenemos el punto de intersección de estas rectas,

x = 1 y y = 3

Supongamos que el punto (1, 3) divide la recta que une (–1, 1) y (5, 7) en la razón 1 : k.

Usando la fórmula de la sección, obtenemos,

(1, 3) = $\left(\frac{k(-1)+1(5)}{1+k},\frac{k(1)+1(7)}{1+k}\right)$

(1, 3) = $\izquierda(\frac{5-k}{1+k},\frac{k+7}{1+k}\derecha)$

Obtenemos,

=> – k + 5 = 1 + k

=> 2k = 4

=> k = 2

Por tanto, la recta que une los puntos (–1, 1) y (5, 7) se divide por la recta x + y = 4 en la razón 1 : 2.

Pregunta 15. Encuentra la distancia de la línea 4x + 7y + 5 = 0 desde el punto (1, 2) a lo largo de la línea 2x – y = 0.

Solución:

Se nos da,

2x – y = 0 . . . . (1)

4x + 7y + 5 = 0 . . . . (2)

Resolviendo (1) y (2), obtenemos el punto de intersección de las rectas,

x = –5/18 y y = –5/9.

Entonces, obtenemos B (–5/18, –5/9) y tenemos A (1, 2). Ahora tenemos que encontrar la distancia AB.

Usando la fórmula de la distancia, obtenemos,

AB = $\sqrt{\left(1+\frac{5}{18}\right)^2+\left(2+\frac{5}{9}\right)^2}{}$

= $\sqrt{\left(\frac{23}{18}\right)^2+\left(\frac{23}{9}\right)^2}$

= $\sqrt{\left(\frac{23}{9}\right)^2\left(\frac{1}{2}\right)^2+\left(\frac{23}{9}\right) ^2}$

= $\frac{23}{9}\sqrt{\frac{1}{4}+1}$

= $\frac{23}{9}\sqrt{\frac{5}{4}}$

= $\frac{23\sqrt{5}}{18}$ unidades

Por lo tanto, la distancia requerida es $\frac{23\sqrt{5}}{18}$ unidades.

Pregunta 16. Encuentra la dirección en la que se debe trazar una línea recta a través del punto (–1, 2) para que su punto de intersección con la línea x + y = 4 esté a una distancia de 3 unidades de este punto.

Solución:

Supongamos que y = mx + c es la línea que pasa por el punto (–1, 2). Entonces obtenemos

=> 2 = m (–1) + c

=> 2 = –m + c

=> do = metro + 2

Poniendo el valor de c en la ecuación, obtenemos,

y = mx + metro + 2 . . . . (1)

Ahora la línea dada es

x + y = 4 . . . . (2)

Resolviendo ambas ecuaciones obtenemos el punto de intersección de estas líneas,

x = $\frac{2-m}{m+1}$ , y = $\frac{5m+2}{m+1}$

Ahora el punto $\left(\frac{2-m}{m+1},\frac{5m+2}{m+1}\right)$ está a una distancia de 3 unidades del punto (–1, 2).

De la fórmula de distancia, obtenemos,

=> $\sqrt{\left(\frac{2-m}{m+1}+1\right)^2+\left(\frac{5m+2}{m+1}-2\right)^2}=3$

=> $\sqrt{\left(\frac{2-m+m+1}{m+1}\right)^2+\left(\frac{5m+2-2m-2}{m+1}\right)^2}=3$

=> $\sqrt{\frac{9}{(m+1)^2}+\frac{9m^2}{(m+1)^2}}=3$

=> $\frac{9}{(m+1)^2}+\frac{9m^2}{(m+1)^2}=9$

=> $\frac{1}{(m+1)^2}+\frac{m^2}{(m+1)^2}=1$

=> $\frac{1+m^2}{(m+1)^2}=1$

=> 1 + metro ² = metro ² + 1 + 2m

=> 2m = 0

=> metro = 0

Como la pendiente de la línea requerida es cero, la línea debe ser paralela al eje x.

Pregunta 17. La hipotenusa de un triángulo rectángulo tiene sus extremos en los puntos (1, 3) y (−4, 1). Encuentra la ecuación de los catetos (lados perpendiculares) del triángulo.

Solución:

Supongamos que △ABC es un triángulo rectángulo donde ∠ C = 90 ^o ym es la pendiente de AC.

Entonces la pendiente de BC = –1/m. Y la ecuación de AC está dada por,

=> y-3 = metro (x-1)

=> x – 1 = 1/m (y – 3)

Sabemos que la ecuación de BC está dada por,

=> y – 1 = – 1/m (x + 4)

=> x + 4 = – metro (y – 1)

Si m = 0, obtenemos las ecuaciones de los lados perpendiculares,

y – 3 = 0 y x + 4 = 0 o,

y = 3 y x = –4

Si m = ∞, obtenemos las ecuaciones,

x – 1 = 0 y y – 1 = 0 o,

x = 1 y y = 1

Pregunta 18. Encuentra la imagen del punto (3, 8) con respecto a la recta x + 3y = 7 suponiendo que la recta sea un espejo plano.

Solución:

se nos da eso

x + 3y = 7 . . . . (1)

Supongamos que B (a, b) es la imagen del punto A (3, 8). Por lo tanto, la línea (1) es la bisectriz perpendicular de AB.

Pendiente de la recta (1) = −1/3

Y pendiente de la línea AB = $\frac{b-8}{a-3}$

Sabemos que AB y la línea (1) son perpendiculares, entonces tenemos,

=> $(\frac{b-8}{a-3})×\frac{-1}{3}=-1$

=> $\frac{b-8}{3a-9}=1$

=> 3a – segundo = 1 . . . . (2)

Ahora, el punto medio de AB = $\left(\frac{a+3}{2},\frac{b+8}{2}\right)$ . Como el punto medio es la línea de satisfacción (1), obtenemos,

=> $(\frac{a+3}{2})+3(\frac{b+8}{2})=7$

=> a + 3 + 3b + 24 = 14

=> un + 3b = −13 . . . . (3)

Resolviendo (2) y (3), obtenemos, a = –1 y b = –4

Por tanto, la imagen del punto dado con respecto a la recta dada es (–1, –4).

Pregunta 19. Si las rectas y = 3x + 1 y 2y = x + 3 tienen la misma inclinación que la recta y = mx + 4, encuentra el valor de m.

Solución:

Se nos da,

y = 3x + 1 . . . . (1)

2y = x + 3 . . . . (2)

y = mx + 4 . . . . (3)

Entonces la pendiente de la línea (1), a = 3,

línea (2), b = 1/2

línea (3), c = m

Se da que las rectas (1) y (2) tienen la misma inclinación que la recta (3) lo que implica que el ángulo entre las rectas (1) y (3) es igual al ángulo entre las rectas (2) y (3).

=> $|\frac{a-c}{1+ac}|=|\frac{b-c}{1+bc}|$

=> $|\frac{3-m}{1+3m}|=|\frac{\frac{1}{2}-m}{1+\frac{m}{2}}|$

=> $|\frac{3-m}{1+3m}|=|\frac{1-2m}{2+m}|$

=> $\frac{3-m}{1+3m}=\pm\left(\frac{1-2m}{2+m}\right)$

=> $\frac{3-m}{1+3m}=\frac{1-2m}{2+m}$ o $\frac{3-m}{1+3m}=\frac{2m-1}{2+m}$

=> $-m^2+m+6=1+m-6m^2$ o $-m^2+m+6=-1-m+6m^2$

=> 5m ² + 5 = 0 (ignorado) o 7m ² − 2m − 7 = 0

=> 7m ² − 2m − 7 = 0

=> metro = $\frac{2\pm2\sqrt{1+49}}{14}$

=> metro = $\frac{1\pm5\sqrt{2}}{7}$

Por lo tanto, el valor requerido de m es $\frac{1\pm5\sqrt{2}}{7}$ .

Pregunta 20. Si la suma de las distancias perpendiculares de un punto variable P (x, y) desde las líneas x + y – 5 = 0 y 3x – 2y + 7 = 0 es siempre 10. Demuestre que P debe moverse en una línea.

Solución:

Nos dan líneas,

x + y – 5 = 0 . . . . (1)

3x – 2y + 7 = 0 . . . . (2)

Ahora, sabemos que la distancia perpendicular (d) de una línea Ax + By + C = 0 desde (x, y) está dada por,

re = $\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$

Entonces, la distancia perpendicular (d ₁ ) de una línea x + y – 5 = 0 desde (x, y) es,

$d_1=\frac{|x+y-5|}{\sqrt{1^2+1^2}}$

= $\frac{|x+y-5|}{\sqrt{2}}$

Y la distancia perpendicular (d ₂ ) de una línea 3x – 2y + 7 = 0 desde (x, y) es,

$d_2=\frac{|3x-2y+7|}{\sqrt{3^2+(-2)^2}}$

= $\frac{|3x-2y+7|}{\sqrt{13}}$

Según la pregunta,

=> re ₁ + re ₂ = 10

=> $\frac{|x+y-5|}{\sqrt{2}}+\frac{|3x-2y+7|}{\sqrt{13}}=10$

=> $\sqrt{13}|x+y-5|+\sqrt{2}|3x-2y+7|-10\sqrt{26}=0$

=> $\sqrt{13}(x+y-5)+\sqrt{2}(3x-2y+7)-10\sqrt{26}=0$

=> $\sqrt{13}x+\sqrt{13}y-5\sqrt{13}+3\sqrt{2}x-2\sqrt{2}y+7\sqrt{2}-10\sqrt{26}=0$

=> $(\sqrt{13}+3\sqrt{2})x+(\sqrt{13}-2\sqrt{2})y+(7\sqrt{2}-5\sqrt{13}-10\sqrt{26})=0$

Como la ecuación representa una recta, P debe moverse sobre una recta.

Por lo tanto, probado.

Pregunta 21. Encuentra la ecuación de la línea que equidista de las líneas paralelas 9x + 6y – 7 = 0 y 3x + 2y + 6 = 0.

Solución:

Somos los dados las líneas,

9x + 6y – 7 = 0 . . . . (1)

3x + 2y + 6 = 0 . . . . (2)

Sean (a, b) el punto que se encuentra sobre la recta equidistante de (1) y (2).

Ahora, sabemos que la distancia perpendicular (d) de una línea Ax + By + C = 0 desde (x, y) está dada por,

$d = \frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$

Entonces, la distancia perpendicular (d ₁ ) de una línea 9x + 6y – 7 = 0 desde (a, b) es,

$d_1=\frac{|9a+6b-7|}{\sqrt{9^2+6^2}}$

= $\frac{|9a+6b-7|}{3\sqrt{13}}$

Y la distancia perpendicular (d ₂ ) de una línea 3x + 2y + 6 = 0 desde (a, b) es,

$d_2=\frac{|3a+2b+6|}{\sqrt{3^2+2^2}}$

= $\frac{|3a+2b+6|}{\sqrt{13}}$

Según la pregunta,

=> re ₁ = re ₂

=> $\frac{|9a+6b-7|}{3\sqrt{13}} = \frac{|3a+2b+6|}{\sqrt{13}}$

=> |9a + 6b − 7| = 3 |3a + 2b + 6|

=> 9h + 6k – 7 = 3 (3h + 2k + 6) o 9h + 6k – 7 = – 3 (3h + 2k + 6)

=> 9h + 6k – 7 = 9h + 6k + 18 o 9h + 6k – 7 = –9h – 6k – 18

=> – 7 = 18 (ignorado) o 18h + 12k + 11 = 0

=> 18h + 12k + 11 = 0

Por lo tanto, la ecuación requerida de la recta es 18x + 12y + 11 = 0.

Pregunta 22. Un rayo de luz que pasa por el punto (1, 2) se refleja en el eje x en el punto A y el rayo reflejado pasa por el punto (5, 3). Encuentre las coordenadas de A.

Solución:

La línea perpendicular a los ejes divide el ∠ BAC = 90 ^o en dos partes iguales, cada una con valor de θ.

Por lo tanto, θ = 45 ^o . Y por lo tanto, las líneas AC y AB subtienden ángulos iguales (θ) en el eje x.

Pendiente de AC = tan θ = $\frac{3}{5-a}$ . . . . (1)

Pendiente de AB = tan (180−θ) = $\frac{2}{1-a}$

=> −tan θ = $\frac{2}{1-a}$

=> bronceado θ = $\frac{2}{a-1}$ . . . . (2)

De (1) y (2), obtenemos,

=> $\frac{3}{5-a} = \frac{2}{a-1}$

=> 3a – 3 = 10 – 2a

=> un = 13/5

Por lo tanto, las coordenadas del punto A son (13/5, 0).

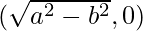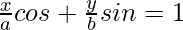Pregunta 23. Demuestra que el producto de las longitudes de las perpendiculares trazadas desde los puntos $(\sqrt{a^2-b^2},0)$ ya $(-\sqrt{a^2-b^2},0)$ la recta $\frac{x}{a}cosθ+\frac{y}{b}sinθ=1$ es b ² .

Solución:

Nos dan la línea,

$\frac{x}{a}cosθ+\frac{y}{b}sinθ=1$

=> bx cos θ + ay pecado θ – ab = 0 . . . . (1)

Ahora, sabemos que la distancia perpendicular (d) de una línea Ax + By + C = 0 desde (x, y) está dada por,

$d = \frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$

Entonces, la distancia perpendicular (d ₁ ) de (1) desde el punto $(\sqrt{a^2-b^2},0)$ es,

$d_1= \frac{|bcosθ(\sqrt{a^2-b^2})+asinθ(0)-ab|}{\sqrt{b^2cos^2θ+a^2sin^2θ}}$

= $\frac{|bcosθ(\sqrt{a^2-b^2})-ab|}{\sqrt{b^2cos^2θ+a^2sin^2θ}}$

Y la distancia perpendicular (d ₂ ) de (1) desde el punto $(-\sqrt{a^2-b^2},0)$ es,

$d_2= \frac{|bcosθ(-\sqrt{a^2-b^2})+asinθ(0)-ab|}{\sqrt{b^2cos^2θ+a^2sin^2θ}}$

= $\frac{|bcosθ(\sqrt{a^2-b^2})+ab|}{\sqrt{b^2cos^2θ+a^2sin^2θ}}$

Ahora, LHS = d ₁ d ₂

= $\frac{|bcosθ(\sqrt{a^2-b^2})-ab|}{\sqrt{b^2cos^2θ+a^2sin^2θ}}×\frac{|bcosθ(\sqrt{a^2-b^2})+ab|}{\sqrt{b^2cos^2θ+a^2sin^2θ}}$

= $\frac{|b^2cos^2θ(a^2-b^2)-a^2b^2|}{b^2cos^2θ+a^2sin^2θ}$

= $\frac{b^2|cos^2θ(a^2-b^2)-a^2|}{b^2cos^2θ+a^2sin^2θ}$

= $\frac{b^2|a^2cos^2θ-b^2cos^2θ-a^2|}{b^2cos^2θ+a^2sin^2θ}$

= $\frac{b^2|a^2(cos^2θ-1)-b^2cos^2θ|}{b^2cos^2θ+a^2sin^2θ}$

= $\frac{b^2|-a^2sin^2θ-b^2cos^2θ|}{b^2cos^2θ+a^2sin^2θ}$

= $\frac{b^2|-(b^2cos^2θ+a^2sin^2θ)|}{b^2cos^2θ+a^2sin^2θ}$

= $\frac{b^2(b^2cos^2θ+a^2sin^2θ)}{b^2cos^2θ+a^2sin^2θ}$

= ^{segundo 2}

= lado derecho

Por lo tanto, probado.

Pregunta 24. Una persona que se encuentra en el cruce (cruce) de dos caminos rectos representados por las ecuaciones 2x – 3y + 4 = 0 y 3x + 4y – 5 = 0 quiere llegar al camino cuya ecuación es 6x – 7y + 8 = 0 en el menor tiempo. Encuentre la ecuación del camino que debe seguir.

Solución:

Se nos da eso,

2x – 3y + 4 = 0 . . . . (1)

3x + 4y – 5 = 0 . . . . (2)

6x – 7y + 8 = 0 . . . . (3)

Se da que la persona está parada en la intersección de los caminos representados por las líneas (1) y (2).

Resolviendo las ecuaciones (1) y (2) obtenemos

x = –1/17 y y = 22/17

Como la distancia perpendicular es la distancia más corta, la persona puede llegar al camino (3) en el menor tiempo si camina a lo largo de la línea perpendicular a (3) desde el punto (-1/17, 22/17).

Ahora, la pendiente de la recta (3) = 6/7

Por tanto, la pendiente de la recta perpendicular a la recta (3) = –1/(6/7) = –7/6

Entonces, la ecuación de la línea que pasa por (–1/17, 22/17) y tiene una pendiente de –7/6 está dada por,

=> $y-\frac{22}{17}=\frac{-7}{6}(x+\frac{1}{17})$

=> 6 (17y – 22) = –7 (17x + 1)

=> 102y – 132 = –119x – 7

=> 1119x + 102y = 125

Por lo tanto, el camino requerido es 119x + 102y = 125.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Soluciones NCERT Clase 11 – Capítulo 10 Líneas rectas – Ejercicio misceláneo en el Capítulo 10 | conjunto 2

Pregunta 13. Demuestra que la ecuación de la recta que pasa por el origen y forma un ángulo θ con la recta y = mx + c es $\frac{y}{x}=\frac{m\pm tanθ}{1\mp tanθ}$ .

Pregunta 14. ¿En qué proporción la recta que une (–1, 1) y (5, 7) se divide por la recta x + y = 4?

Pregunta 15. Encuentra la distancia de la línea 4x + 7y + 5 = 0 desde el punto (1, 2) a lo largo de la línea 2x – y = 0.

Pregunta 16. Encuentra la dirección en la que se debe trazar una línea recta a través del punto (–1, 2) para que su punto de intersección con la línea x + y = 4 esté a una distancia de 3 unidades de este punto.

Pregunta 17. La hipotenusa de un triángulo rectángulo tiene sus extremos en los puntos (1, 3) y (−4, 1). Encuentra la ecuación de los catetos (lados perpendiculares) del triángulo.

Pregunta 18. Encuentra la imagen del punto (3, 8) con respecto a la recta x + 3y = 7 suponiendo que la recta sea un espejo plano.

Pregunta 19. Si las rectas y = 3x + 1 y 2y = x + 3 tienen la misma inclinación que la recta y = mx + 4, encuentra el valor de m.

Pregunta 20. Si la suma de las distancias perpendiculares de un punto variable P (x, y) desde las líneas x + y – 5 = 0 y 3x – 2y + 7 = 0 es siempre 10. Demuestre que P debe moverse en una línea.

Pregunta 21. Encuentra la ecuación de la línea que equidista de las líneas paralelas 9x + 6y – 7 = 0 y 3x + 2y + 6 = 0.

Pregunta 22. Un rayo de luz que pasa por el punto (1, 2) se refleja en el eje x en el punto A y el rayo reflejado pasa por el punto (5, 3). Encuentre las coordenadas de A.

Pregunta 23. Demuestra que el producto de las longitudes de las perpendiculares trazadas desde los puntos $(\sqrt{a^2-b^2},0)$ ya $(-\sqrt{a^2-b^2},0)$ la recta $\frac{x}{a}cosθ+\frac{y}{b}sinθ=1$ es b ² .

Pregunta 24. Una persona que se encuentra en el cruce (cruce) de dos caminos rectos representados por las ecuaciones 2x – 3y + 4 = 0 y 3x + 4y – 5 = 0 quiere llegar al camino cuya ecuación es 6x – 7y + 8 = 0 en el menor tiempo. Encuentre la ecuación del camino que debe seguir.

Deja una respuesta Cancelar la respuesta

Pregunta 13. Demuestra que la ecuación de la recta que pasa por el origen y forma un ángulo θ con la recta y = mx + c es .

Pregunta 14. ¿En qué proporción la recta que une (–1, 1) y (5, 7) se divide por la recta x + y = 4?

Pregunta 15. Encuentra la distancia de la línea 4x + 7y + 5 = 0 desde el punto (1, 2) a lo largo de la línea 2x – y = 0.

Pregunta 16. Encuentra la dirección en la que se debe trazar una línea recta a través del punto (–1, 2) para que su punto de intersección con la línea x + y = 4 esté a una distancia de 3 unidades de este punto.

Pregunta 17. La hipotenusa de un triángulo rectángulo tiene sus extremos en los puntos (1, 3) y (−4, 1). Encuentra la ecuación de los catetos (lados perpendiculares) del triángulo.

Pregunta 18. Encuentra la imagen del punto (3, 8) con respecto a la recta x + 3y = 7 suponiendo que la recta sea un espejo plano.

Pregunta 19. Si las rectas y = 3x + 1 y 2y = x + 3 tienen la misma inclinación que la recta y = mx + 4, encuentra el valor de m.

Pregunta 20. Si la suma de las distancias perpendiculares de un punto variable P (x, y) desde las líneas x + y – 5 = 0 y 3x – 2y + 7 = 0 es siempre 10. Demuestre que P debe moverse en una línea.

Pregunta 21. Encuentra la ecuación de la línea que equidista de las líneas paralelas 9x + 6y – 7 = 0 y 3x + 2y + 6 = 0.

Pregunta 22. Un rayo de luz que pasa por el punto (1, 2) se refleja en el eje x en el punto A y el rayo reflejado pasa por el punto (5, 3). Encuentre las coordenadas de A.

Pregunta 23. Demuestra que el producto de las longitudes de las perpendiculares trazadas desde los puntos ya la recta es b 2 .

Pregunta 24. Una persona que se encuentra en el cruce (cruce) de dos caminos rectos representados por las ecuaciones 2x – 3y + 4 = 0 y 3x + 4y – 5 = 0 quiere llegar al camino cuya ecuación es 6x – 7y + 8 = 0 en el menor tiempo. Encuentre la ecuación del camino que debe seguir.

Deja una respuesta Cancelar la respuesta

Pregunta 13. Demuestra que la ecuación de la recta que pasa por el origen y forma un ángulo θ con la recta y = mx + c es $\frac{y}{x}=\frac{m\pm tanθ}{1\mp tanθ}$ .

Pregunta 23. Demuestra que el producto de las longitudes de las perpendiculares trazadas desde los puntos $(\sqrt{a^2-b^2},0)$ ya $(-\sqrt{a^2-b^2},0)$ la recta $\frac{x}{a}cosθ+\frac{y}{b}sinθ=1$ es b ² .