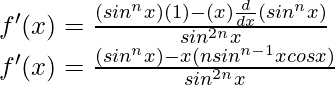Encuentre la derivada de las siguientes funciones (se debe entender que a, b, c, d, p, q, r y s son constantes fijas distintas de cero y m y n son números enteros):
Pregunta 16: 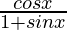
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Pregunta 17: 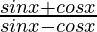
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Pregunta 18: 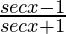
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Pregunta 19: sen n x
Solución:
f(x) = sen n x
Cuando n = 1,
f(x) = sen x
Cuando n = 2,
f(x) = sen 2 x = sen x sen x
Usando la regla del producto, tenemos
(uv)’ = uv’+vu’
f'(x) = (sen x) (cos x) + (sen x) (cos x) = 2 sen x cos x
Cuando n = 3,
f(x) = sen 3 x = sen 2 x sen x
Usando la regla del producto, tenemos
(uv)’ = uv’+vu’
El patrón wrt n se ve aquí, de la siguiente manera
Revisemos esta afirmación.
Para P(n) = n sen n-1 x cos x
Para P(1),
P(1) = 1 sen 1-1 x cos x = cos x. Cual es verdad.
n = k
norte = k+1
Usando la regla del producto, tenemos
(uv)’ = uv’+vu’
= (sen k x)
+ (sen x)
= (sen k x) (cos x) + (sen x) (k sen k-1 x cos x)
= (sen k x) (cos x)[k+1]
Por lo tanto probado para P(k+1).
Entonces,
es cierto.
Pregunta 20: 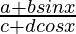
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 21: 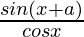
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Tomemos g(x) = sin (x+a)
g(x+h) = sen((x+h)+a)
Del primer principio,
Usando la identidad trigonométrica,
sen A – sen B = 2 cos
sen
Multiplicamos y dividimos por 2, tenemos
Por eso,
Usando la identidad trigonométrica,
cos A cos B + sen A sen B = cos (AB)
Pregunta 22: x 4 (5sen x – 3cos x)
Solución:
f(x) = x 4 (5sen x – 3cos x)
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + vu’
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
f'(x) = (x 4 ) [(5 cos x) – (3 (- sen x))] + (5 sen x – 3 cos x)(4x 3 )
f'(x) = (x 4 ) [(5 cos x) + (3 sen x)] + (5 sen x – 3 cos x)(4x 3 )
f'(x) = (x 3 ) [5x cos x + 3x sen x + 20 sen x – 12 cos x]
Pregunta 23: (x 2 +1) cos x
Solución:
f(x) = (x 2 +1) porque x
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + vu’
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
f'(x) = (x 2 +1) (- sen x) + (cos x)[(2x 2-1 )+0]
f'(x) = -x 2 sen x- sen x + 2x cos x
Pregunta 24: 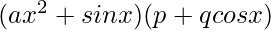
Solución:
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + vu’
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 25: (x + cos x)(x – tan x)
Solución:
f(x) = (x + cos x)(x – tan x)
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + vu’
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Tomemos g(x) = tan x
Del primer principio,
Usando la identidad trigonométrica,
sen a cos b – cos a sen b = sen (ab)
g'(x) = segundo 2 x
Por eso,
f'(x) = (x + cos x)
+ (x – tan x)[1 + (- sen x)]
f'(x) = (x + cos x) [1 – (seg 2 x)] + (x – tan x)[1 – sen x]
f'(x) = (x + cos x) [tan 2 x] + (x – tan x)[1 – sen x]
f'(x) = tan 2 x (x + cos x) + (x – tan x)[1 – sen x]
Pregunta 26: 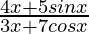
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 27: 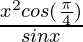
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 28: 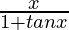
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Tomemos g(x) = tan x
Del primer principio,
Usando la identidad trigonométrica,
sen a cos b – cos a sen b = sen (ab)
g'(x) = segundo 2 x
Por eso,
Pregunta 29: (x + seg x) (x-tan x)
Solución:
f(x) = (x + seg x) (x-tan x)
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + vu’
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Tomemos g(x) = tan x
Del primer principio,
Usando la identidad trigonométrica,
sen a cos b – cos a sen b = sen (ab)
g'(x) = segundo 2 x
Ahora, tomemos h(x) = sec x =
h(x+h) =
Del primer principio,
Usando la identidad trigonométrica,
cos a – cos b = -2 sen
sen
Multiplicamos y dividimos por 2, tenemos
Por eso,
Pregunta 30: 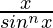
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Tomemos, g(x) = sen x
Cuando n = 1,
g(x) = sen x
Cuando n = 2,
Usando la regla del producto, tenemos
(uv)’ = uv’+vu’
g'(x) = (sen x) (cos x) + (sen x) (cos x) = 2 sen x cos x
Cuando n = 3,
g(x) = sen 3 x = sen 2 x sen x
Usando la regla del producto, tenemos
(uv)’ = uv’+vu’
El patrón wrt n se ve aquí, de la siguiente manera
Revisemos esta afirmación.
Para
Para P(1),
. Cual es verdad.
n = k
norte = k+1
Usando la regla del producto, tenemos
(uv)’ = uv’+vu’
Por lo tanto probado para P(k+1).
Entonces,
es cierto.
Entonces, la ecuación dada será
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
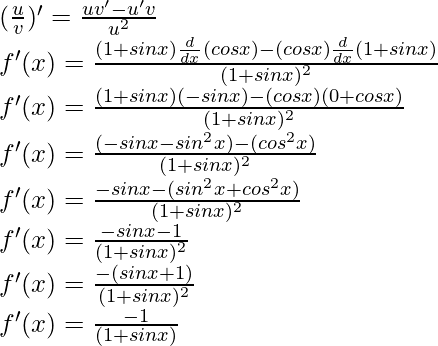
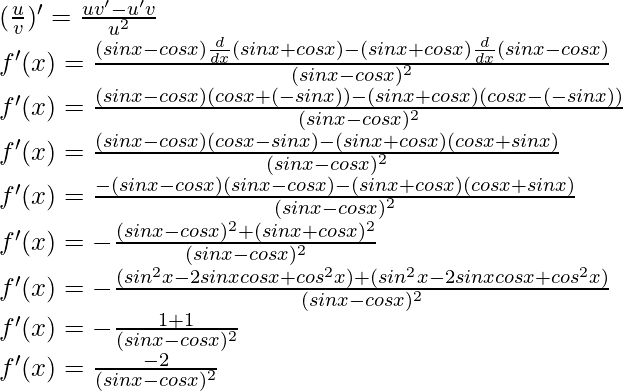
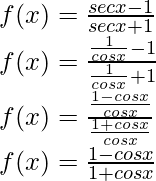
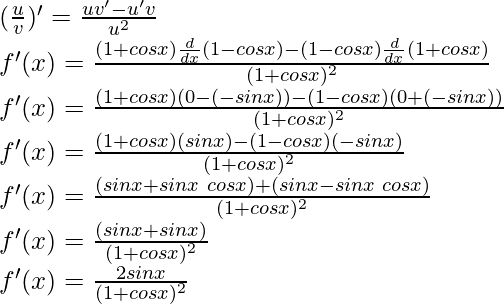
![Rendered by QuickLaTeX.com f'(x) = (sin^2 x) \frac{d}{dx}(sin x) + (sin x) \frac{d}{dx}(sin^2 x)\\ f'(x) = (sin^2 x) (cos x) + (sin x) (2 sin x\hspace{0.1cm} cos x)\\ f'(x) = (sin^2 x \hspace{0.1cm}cos x) + (2 sin^2 x \hspace{0.1cm}cos x)\\ f'(x) = (sin^2 x\hspace{0.1cm} cos x)[1+2]\\ f'(x) = 3 sin^2 x \hspace{0.1cm}cos x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7318a781107414de49f8b50281887a40_l3.png)
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-u'v}{u^2}\\ f'(x) = \frac{(c+dcos x) \frac{d}{dx}(a+bsin x) - (a+bsin x)\frac{d}{dx}(c+dcos x)}{(c+dcos x)^2}\\ f'(x) = \frac{(c+dcos x) [\frac{d}{dx}(a)+\frac{d}{dx}(bsin x)] - (a+bsin x)\frac{d}{dx}(c)+\frac{d}{dx}(dcos x)}{(c+dcos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b385a146653a12a77170fd1f7540fe6a_l3.png)
![Rendered by QuickLaTeX.com f'(x) = \frac{(c+dcos x) [0+b cos x] - (a+bsin x)[0+(-d sin x)]}{(c+dcos x)^2}\\ f'(x) = \frac{(c+dcos x) (b cos x) + (a+bsin x)(d sin x)}{(c+dcos x)^2}\\ f'(x) = \frac{(bc\hspace{0.1cm} cos x+db\hspace{0.1cm} cos^2 x) + (ad\hspace{0.1cm} sin x+db\hspace{0.1cm} sin^2 x)}{(c+d\hspace{0.1cm}cos x)^2}\\ f'(x) = \frac{(bc\hspace{0.1cm} cos x + db (cos^2 x + sin ^2 x) + ad \hspace{0.1cm}sin x)}{(c+d\hspace{0.1cm}cos x)^2}\\ f'(x) = \frac{(bc\hspace{0.1cm} cos x + db+ ad\hspace{0.1cm} sin x)}{(c+d\hspace{0.1cm}cos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46bd8855bec22fa2d46a628c4dbe310b_l3.png)
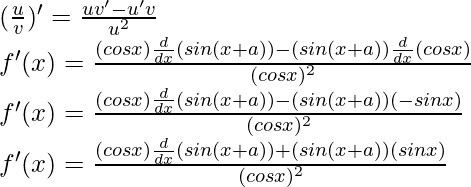
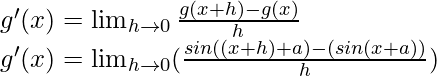
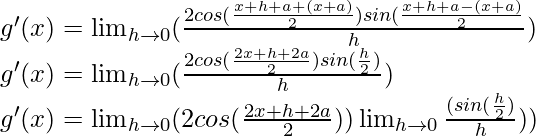
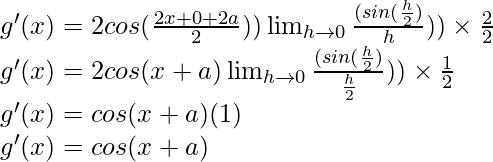
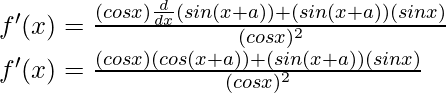
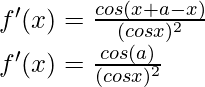
![Rendered by QuickLaTeX.com f'(x) = (ax^2+sin x) \frac{d}{dx}(p+q cos x) + (p+q cos x)\frac{d}{dx}((ax^2+sin x))\\ f'(x) = (ax^2+sin x) [\frac{d}{dx}(p)+\frac{d}{dx}(q cos x)] + (p+q cos x)[\frac{d}{dx}(ax^2)+\frac{d}{dx}(sin x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ad2ca3a846a021eeace67eccf1bc6e1_l3.png)
![Rendered by QuickLaTeX.com f'(x) = (ax^2+sin x) [0+q(- sin x)] + (p+q cos x)[a(2x^{2-1})+(cos x)]\\ f'(x) = (ax^2+sin x) (- q sin x) + (p+q cos x)[2ax+cos x]\\ f'(x) = - q sin x(ax^2 + sin x) + (p+q cos x)[2ax+cos x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d74156a985e6824124fdb882a135d9dc_l3.png)
![Rendered by QuickLaTeX.com f'(x) = (x + cos x) \frac{d}{dx}(x - tan x) + (x - tan x)\frac{d}{dx}(x + cos x)\\ f'(x) = (x + cos x) [\frac{d}{dx}(x) - \frac{d}{dx}(tan x)] + (x - tan x)[\frac{d}{dx}(x) + \frac{d}{dx}(cos x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6ef2bab372d3afe1d311ed812d337b58_l3.png)
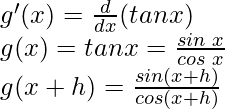
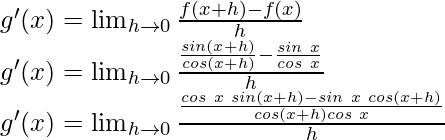
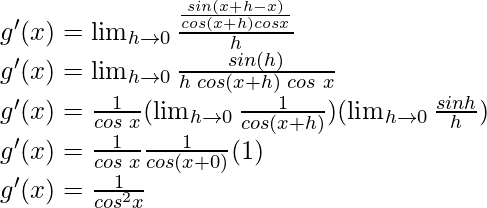
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-u'v}{u^2}\\ f'(x) = \frac{(3x+7cos x) \frac{d}{dx}(4x+5sin x) - (4x+5sin x)\frac{d}{dx}(3x+7cos x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(3x+7cos x) [\frac{d}{dx}(4x)+\frac{d}{dx}(5sin x)] - (4x+5sin x)[\frac{d}{dx}(3x)+\frac{d}{dx}(7cos x)]}{(3x+7cos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b2551887531c708c54d6ab99107e0c97_l3.png)
![Rendered by QuickLaTeX.com f'(x) = \frac{(3x+7cos x) [4+(5 cos x)] - (4x+5sin x)[3 + 7(- sin x)]}{(3x+7cos x)^2}\\ f'(x) = \frac{(3x+7cos x) [4+5 cos x] - (4x+5sin x)[3 - 7 sin x]}{(3x+7cos x)^2}\\ f'(x) = \frac{(12x+28 cos x+15x cos x + 35 cos^2x) - [(12x + 15sin x)-(28x sin x + 35 sin^2 x)]}{(3x+7cos x)^2}\\ f'(x) = \frac{(12x+28 cos x+15x cos x + 35 cos^2x)- (12x + 15sin x-28x sin x - 35 sin^2 x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(12x+28 cos x+15x cos x + 35 cos^2x - 12x - 15sin x+28x sin x + 35 sin^2 x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(28 cos x+15x cos x + 35 (cos^2x + sin^2x) - 15sin x + 28x sin x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(28 cos x+15x cos x + 35 - 15sin x + 28x sin x)}{(3x+7cos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6262ca65e274d5f9288b4302ad1a7f9_l3.png)
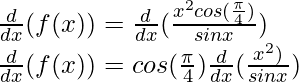
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-u'v}{u^2}\\ f'(x) = (cos(\frac{\pi}{4}) [\frac{(sin x) \frac{d}{dx}(x^2) - (x^2)\frac{d}{dx}(sin x)}{(sin x)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4630855cb1ab1f6fcec8480e6b85e449_l3.png)
![Rendered by QuickLaTeX.com f'(x) = cos(\frac{\pi}{4}) [\frac{(sin x) (2x^{2-1}) - (x^2) (cos x)}{(sin x)^2}]\\ f'(x) = cos(\frac{\pi}{4}) [\frac{2x sin x - x^2 cos x)}{(sin x)^2}]\\ f'(x) = [\frac{(x cos(\frac{\pi}{4})(2 sin x - x cos x)}{(sin x)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b6c5c2fdd80b09687c0d4eee25c41f1_l3.png)
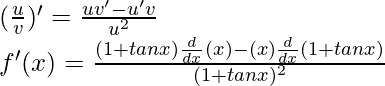
![Rendered by QuickLaTeX.com f'(x) = \frac{(1+tan x) (1) - (x)[\frac{d}{dx}(1)+\frac{d}{dx}(tan x)]}{(1+tan x)^2}\\ f'(x) = \frac{(1+tan x) - (x)[0+\frac{d}{dx}(tan x)]}{(1+tan x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a1e4edc5163be4ad89497e7813626b9_l3.png)
![Rendered by QuickLaTeX.com f'(x) = \frac{(1+tan x) - (x)[0+\frac{d}{dx}(tan x)]}{(1+tan x)^2}\\ f'(x) = \frac{1+tan x - x sec^2x}{(1+tan x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-afc6b8b8ed22828c52bd691f1f27dba5_l3.png)
![Rendered by QuickLaTeX.com f'(x) = (x + sec x) \frac{d}{dx}(x - tan x) + (x - tan x)\frac{d}{dx}(x + sec x)\\ f'(x) = (x + sec x) [\frac{d}{dx}(x) - \frac{d}{dx}(tan x)] + (x - tan x)[\frac{d}{dx}(x) + \frac{d}{dx}(sec x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3246e6877fa563cac5371c851d22e966_l3.png)
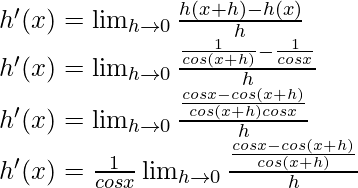
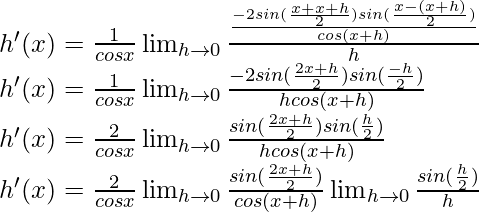
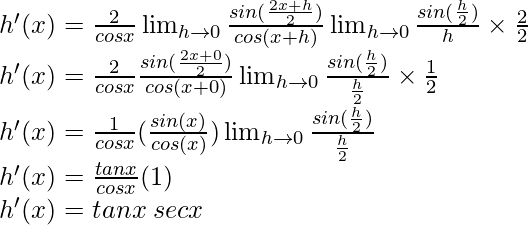
![Rendered by QuickLaTeX.com f'(x) = (x + sec x) [1 - \frac{d}{dx}(tan x)] + (x - tan x)[1 + \frac{d}{dx}(sec x)]\\ f'(x) = (x + sec x) [1 - (sec^2x)] + (x - tan x)[1 + (sec x \hspace{0.1cm}tan x)]\\ f'(x) = (x + sec x) [tan^2x)] + (x - tan x)[1 + (sec x \hspace{0.1cm}tan x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a95429721ec241fbe6034284cb43d171_l3.png)
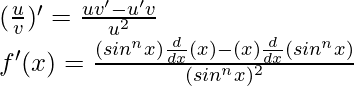
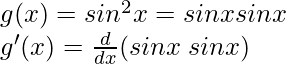
![Rendered by QuickLaTeX.com g'(x) = (sin^2 x) \frac{d}{dx}(sin x) + (sin x) \frac{d}{dx}(sin^2 x)\\ g'(x) = (sin^2 x) (cos x) + (sin x) (2 sin x \hspace{0.1cm}cos x)\\ g'(x) = (sin^2 x \hspace{0.1cm}cos x) + (2 sin^2 x\hspace{0.1cm} cos x)\\ g'(x) = (sin^2 x\hspace{0.1cm} cos x)[1+2]\\ g'(x) = 3 sin^2 x\hspace{0.1cm} cos x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0f6118724449ba9d0dba633eb0a8d1b_l3.png)
![Rendered by QuickLaTeX.com = (sin^k x) \frac{d}{dx}(sin x) + (sin x) \frac{d}{dx}(sin^k x)\\ = (sin^k x) (cos x) + (sin x) (k sin^{k-1}x \hspace{0.1cm}cos x)\\ = (sin^k x) (cos x)[k+1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cd8f985d319e1a753c26b6e23b1d92e_l3.png)