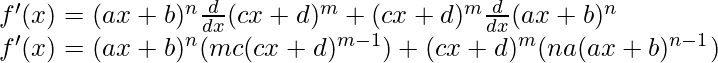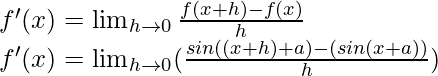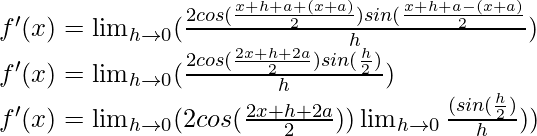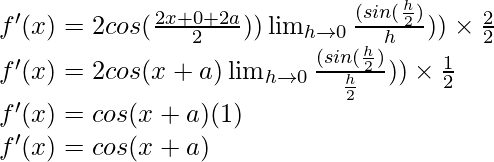Pregunta 1: Encuentra la derivada de las siguientes funciones a partir del primer principio:
(yo) -x
Solución:
f(x) = -x
f(x+h) = -(x+h)
Del primer principio,
f'(x) = -1
(ii) (-x) -1
Solución:
f(x) = (-x) -1 =
f(x+h) = (-(x+h)) -1 =
Del primer principio,
(iii) sen(x+1)
Solución:
f(x) = sen(x+1)
f(x+h) = sen((x+h)+1)
Del primer principio,
Usando la identidad trigonométrica,
sen A – sen B = 2 cos
sen
Multiplicamos y dividimos por 2, tenemos
f'(x) = cos (x+1) (1)
f'(x) = cos (x+1)
(iv) 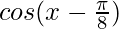
Solución:
Aquí,
Del primer principio,
Usando la identidad trigonométrica,
cos a – cos b = -2 sen
sen
Multiplicando y buceando por 2,
Encuentre la derivada de las siguientes funciones (se debe entender que a, b, c, d, p, q, r y s son constantes fijas distintas de cero y m y n son números enteros):
Pregunta 2: (x+a)
Solución:
f(x) = x+a
Derivando ambos lados,
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 3: 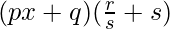
Solución:
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’+u’v
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 4: (ax+b) (cx+d) 2
Solución:
f(x) = (ax+b) (cx+d) 2
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’+u’v
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 5: 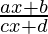
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 6: 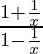
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 7: 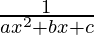
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 8: 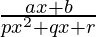
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 9: 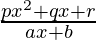
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 10: 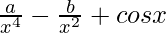
Solución:
Derivando ambos lados,
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 11: 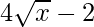
Solución:
Derivando ambos lados,
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 12: (ax+b) n
Solución:
f(x) = (ax+b) norte
f(x+h) = (a(x+h)+b) norte
f(x+h) = (ax+ah+b) norte
Del primer principio,
Usando la expansión binomial, tenemos
Pregunta 13: (ax+b) n (cx+d) m
Solución:
f(x) = (ax+b) norte (cx+d) metro
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’+u’v
Tomemos, g(x) = (cx+d) m
g(x+h) = (c(x+h)+d) metro
g(x+h) = (cx+ch+d) m
Del primer principio,
Usando la expansión binomial, tenemos
Así como
Pregunta 14: sen (x + a)
Solución:
f(x) = sen(x+a)
f(x+h) = sin((x+h)+a)
Del primer principio,
Usando la identidad trigonométrica,
sen A – sen B = 2 cos
sen
Multiplicamos y dividimos por 2, tenemos
Pregunta 15: cosec x cot x
Solución:
f(x) = cosec x cot x
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’+u’v
f'(x) = cot x (-cot x cosec x) + (cosec x) (-cosec 2 x)
f'(x) = – cot 2 x cosec x – cosec 3 x
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
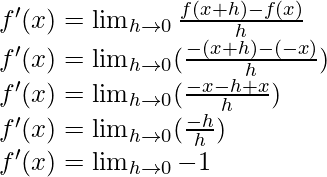
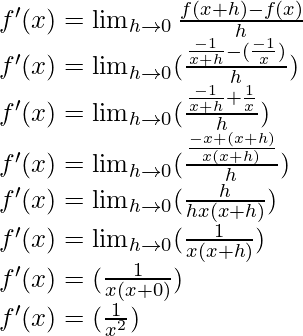
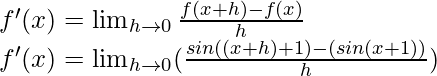
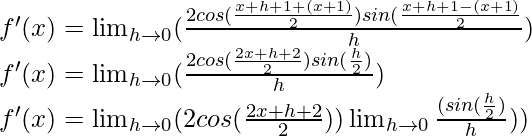
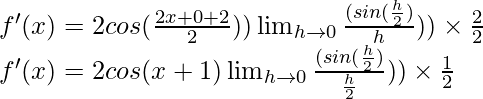
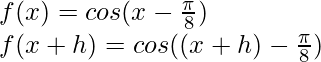
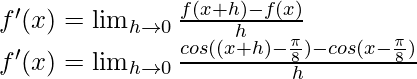
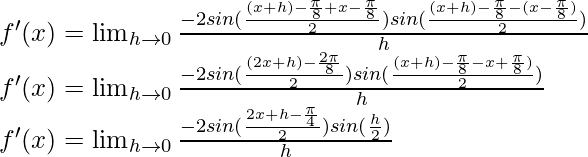

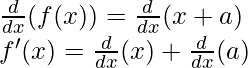
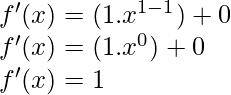
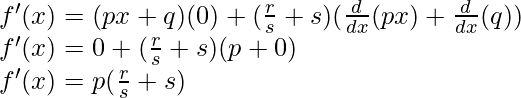
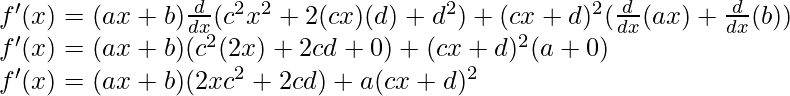
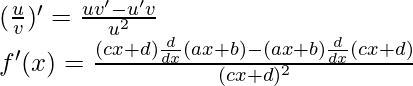
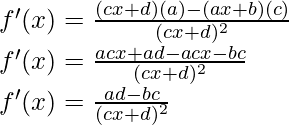
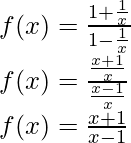
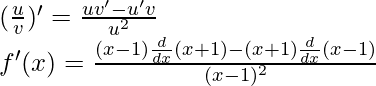
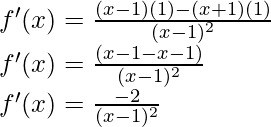
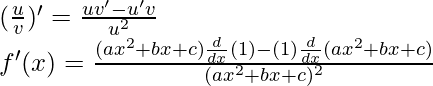
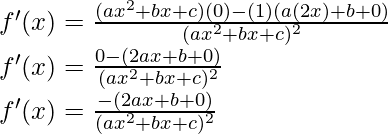
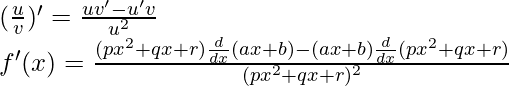
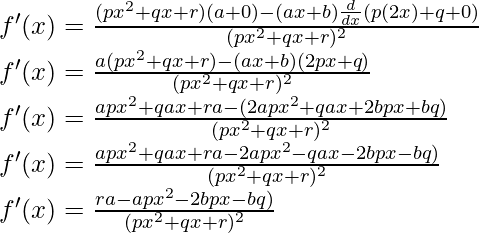
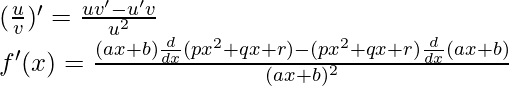
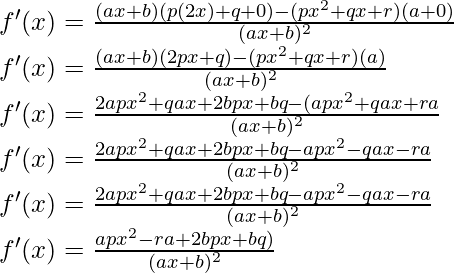
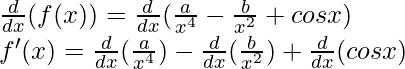
![Rendered by QuickLaTeX.com f'(x) = a \frac{d}{dx}(x^{-4}) - b\frac{d}{dx}(x^{-2})+(- sin x)\\ f'(x) = a (-4x^{-4-1}) - b((-2)x^{-2-1})+(- sin x)\\ f'(x) = a (-4x^{-5}) - b((-2)x^{-3})+(- sin x)\\ f'(x) = -[4ax^{-5} - 2bx^{-3} + sin x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ab5d3ca2f48977416005ce986aa7ee7_l3.png)
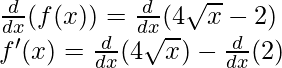
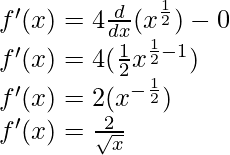
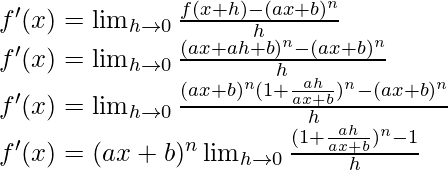
![Rendered by QuickLaTeX.com f'(x) = (ax+b)^n \lim_{h \to 0} \frac{[1+n(\frac{ah}{ax+b}+\frac{n(n-1)}{2!}(\frac{ah}{(ax+b)^2}+.....]-1}{h}\\ f'(x) = (ax+b)^n \lim_{h \to 0} \frac{[n(\frac{ah}{ax+b}+\frac{n(n-1)a^2h^2}{2!(ax+b)^2}+.................]}{h}\\ f'(x) = (ax+b)^n \lim_{h \to 0} [n(\frac{a}{ax+b}+\frac{n(n-1)a^2h}{2!(ax+b)^2}+.................]\\ f'(x) = (ax+b)^n [n(\frac{a}{ax+b}+\frac{n(n-1)a^2(0)}{2!(ax+b)^2}+0+0+0......]\\ f'(x) = (ax+b)^n (\frac{na}{ax+b})\\ f'(x) = na (ax+b)^{n-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5111de4b3cabfb330f5fa7ccfbc4c249_l3.png)
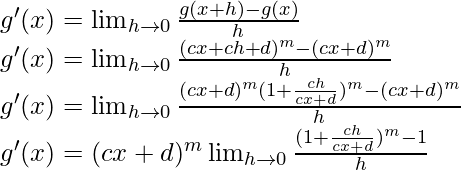
![Rendered by QuickLaTeX.com g'(x) = (cx+d)^m \lim_{h \to 0} \frac{[1+m(\frac{ch}{cx+d}+\frac{m(m-1)}{2!}(\frac{ch}{(cx+d})^2+.....)]-1}{h}\\ g'(x) = (cx+d)^m \lim_{h \to 0} \frac{[m(\frac{ch}{cx+d}+\frac{m(nm-1)c^2h^2}{2!(cx+d)^2}+.................)]}{h}\\ g'(x) = (cx+d)^m \lim_{h \to 0} [m(\frac{c}{cx+d}+\frac{m(m-1)c^2h}{2!(cx+d)^2}+.................)]\\ g'(x) = (cx+d)^m [m(\frac{c}{cx+d}+\frac{m(m-1)c^2(0)}{2!(cx+d)^2}+0+0+0......)]\\ g'(x) = (cx+d)^m (\frac{mc}{cx+d})\\ g'(x) = mc (cx+d)^{m-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c778c55d5223983e04e541b252d9202_l3.png)