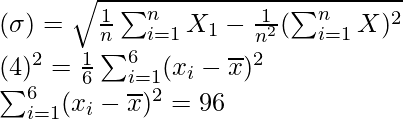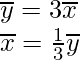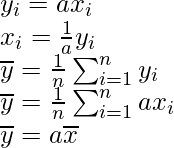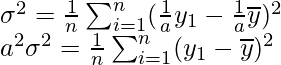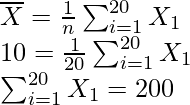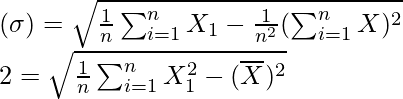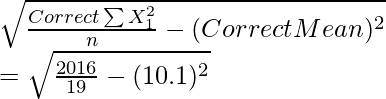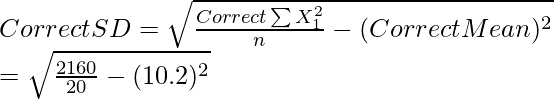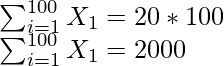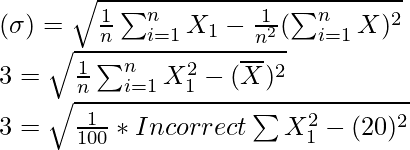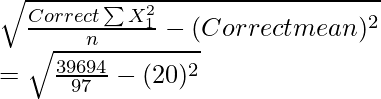Pregunta 1. La media y la varianza de ocho observaciones son 9 y 9,25, respectivamente. Si seis de las observaciones son 6, 7, 10, 12, 12 y 13, encuentre las dos observaciones restantes.
Solución:
Dado,
Disponemos de seis de las observaciones 6, 7, 10, 12, 12 y 13.
Supongamos que las observaciones que faltan son a y b.
Ahora, Media
= 9
9 = (6 + 7 + 10 + 12 + 12 + 13 + a + b)/8
Pero,
Resolviendo a + b, obtenemos,
a + b = 12
También,
Diferencia
equiparar
Tenemos,
9.25 = 1/8(6 2 + 7 2 + 10 2 + 12 2 + 12 2 + 13 2 + a 2 + b 2 ) – 9 2
=> 9,25 + 81 = 1/8(36 + 49 + 100 + 144 + 144 + 169 + a 2 + b 2 )
=> 90,25 * 8 = 642 + un 2 + segundo 2
=> un 2 + segundo 2 = 80
Tenemos, b = 12 – a
Al sustituir el valor,
un 2 + (12 – un) 2 = 80
=> 2a 2 – 24a + 64 = 0
Al dividir por 2, obtenemos
un 2 – 12a + 32 = 0
Por lo tanto, a = 4, 8
Ahora, para a = 4, b = 8
Y, para a = 8, b = 4
Pregunta 2. La media y la varianza de 7 observaciones son 8 y 16, respectivamente. Si cinco de las observaciones son 2, 4, 10, 12, 14. Encuentra las dos observaciones restantes.
Solución:
Dado,
Contamos con cinco de las observaciones 2, 4, 10, 12, 14.
Supongamos que las observaciones que faltan son a y b.
Ahora, malo
Pero,
8 = (2 + 4 + 10 + 12 + 14 + a + b)/(7)
Resolviendo a + b, obtenemos,
a + b = 14
También,
Varianza =
equiparar
Tenemos,
16 = 1/7(2 2 + 4 2 + 10 2 + 12 2 + 14 2 + un 2 + segundo 2 ) – 64
=> 16 + 64 = 1/7(4 + 16 + 100 + 144 + 196 + a 2 + b 2 )
=> 560 = 460 + un 2 + segundo 2
=> un 2 +b 2 = 100
Tenemos, b = 14 – a
Al sustituir el valor, obtenemos
un 2 + (14 – un) 2 = 100
=> 2a 2 – 28a + 96 = 0
Al dividir por 2, obtenemos
un 2 – 14a + 48 = 0
=> (un – 8)(un – 6) = 0
Por lo tanto, a = 6, 8
Ahora, para a = 6, b = 8
Y, para a = 8, b = 6
Pregunta 3. La media y la desviación estándar de seis observaciones son 8 y 4, respectivamente. Si cada observación se multiplica por 3, encuentre la nueva media y la nueva desviación estándar de las observaciones resultantes.
Solución:
Media de seis observaciones = 8
Desviación estándar de seis observaciones = 4
Sean las seis observaciones x 1 , x 2 , x 3 , x 4 , x 5 , x 6
Por lo tanto,
Media de las observaciones,
= (x 1 + x 2 + x 3 + x 4 + x 5 + x 6 )/6 = 8
Si cada observación se multiplica por 3 y las observaciones resultantes son y i entonces,
y yo = 3x yo
x i = (1/3) y i , donde i = 1….6
Entonces, nueva media
= (y1 + y2 + y3 + y4 + y5 + y6 ) / 6
= 3(x1 + x2 + x3 + x4 + x5 + x6 ) / 6
= 3 * 8
= 24
Desviación Estándar
Sustituyendo valores, obtenemos,
Por lo tanto,
Varianza de la nueva observación = 1/6 x 864
= 144
Desviación Estándar = √144
= 12
Pregunta 4. Dado que x̅ es la media y σ 2 es la varianza de n observaciones x 1 , x 2 , …,x n . Demuestre que la media y la varianza de las observaciones ax 1 , ax 2 , ax 3 , …., ax n son ax̅ y a 2 σ 2 , respectivamente, (a ≠ 0).
Solución:
Supongamos que las observaciones son x 1 , …x n
Media de n observaciones =
Varianza de n observaciones =
Sabemos,
y
Ahora,
Media de las observaciones, ax 1 , ax 2 , …..ax n =
Sustituyendo valores, obtenemos,
Varianza =
Pregunta 5. Se encuentra que la media y la desviación estándar de 20 observaciones son 10 y 2, respectivamente. Al volver a verificar, se encontró que una observación 8 era incorrecta. Calcule la media y la desviación estándar correctas en cada uno de los siguientes casos: (i) Si se omite el elemento incorrecto. (ii) Si se reemplaza por 12
Solución:
(i) Por omisión de elemento incorrecto
norte = 20
Media incorrecta = 20
SD incorrecta = 2
Ahora,
Suma incorrecta de observaciones = 200
Suma correcta de observaciones = 200 – 8 = 192
Por lo tanto,
Media correcta = Suma correcta/19
= 192/19
= 10,1
Desviación Estándar
4 = 1/20 Incorrecto
– 100
Incorrecto
= 2080
Por lo tanto,
Correcto
= Incorrecto
– (8) 2
= 2080 – 64
= 2016
Cálculo de la desviación estándar correcta,
SD correcta =
= √(1061,1 – 102,1)
= 2,02
(ii) Si se reemplaza por 12,
Suma incorrecta de observaciones, n = 200
Suma correcta de observaciones n = 200 – 8 + 12
n = 204
Media correcta = Suma correcta / 20
= 204/20
= 10,2
Desviación Estándar
4 = 1/20 Incorrecto
– 100
Incorrecto
= 2080
Por lo tanto, Correcto
= Incorrecto
– (8) 2 + (12) 2
= 2080 – 64 + 144
= 2160
Cálculo de la desviación estándar correcta,
= √(108 – 104,04)
= 1,98
Pregunta 6. La media y la desviación estándar de las notas obtenidas por 50 alumnos de una clase en tres materias, Matemáticas, Física y Química, se dan a continuación:
¿Cuál de las tres materias muestra la mayor variabilidad en las calificaciones y cuál muestra la menor?
| Tema | Matemáticas | Física | Química |
| Significar | 42 | 32 | 40,9 |
| Desviación Estándar | 12 | 15 | 20 |
Solución:
valores dados,
Media de Matemáticas = 42
Desviación estándar de Matemáticas = 12
Media de Física = 32
Desviación estándar de la física = 15
Media de Química = 40.9
Desviación estándar de la química = 20
Ahora,
Coeficiente de variación (CV) =
CV para Matemáticas = 12/42 x 100 = 28,57
CV para Física = 15/32 x 100 = 46,87
CV para Química = 20/40,9 x 100 = 48,89
La Mayor Variabilidad de la asignatura es de Química.
Pregunta 7. Se encontró que la media y la desviación estándar de un grupo de 100 observaciones eran 20 y 3, respectivamente. Más tarde se encontró que tres observaciones eran incorrectas, las cuales se registraron como 21, 21 y 18. Halle la media y la desviación estándar si se omiten las observaciones incorrectas.
Solución:
Dado:
n = 100
Media incorrecta, (x̅) = 20
Desviación estándar incorrecta (σ) = 3
Por lo tanto,
Al resolver obtenemos
Suma incorrecta de observaciones = 2000
Ahora, Suma correcta de observaciones = 2000 – 21- 21 – 18
= 1940
Media correcta = Suma correcta / 97
= 1940/97
= 20
También,
Desviación Estándar
Incorrecto
= 100(9 + 400)
Incorrecto
= 40900
Correcto
= Incorrecto
– (21) 2 – (21) 2 – (18) 2
= 40900 – 441 – 441 – 324
= 40900 – 1206
= 39694
Por lo tanto,
SD correcta =
= √(409.216 – 400)
= 3.036
Publicación traducida automáticamente
Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA