Pregunta 14: 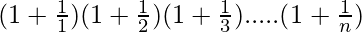 = (n+1)
= (n+1)
Solución:
Tenemos,
P(n) =
= (n+1)
Para n=1 , obtenemos
P(1) = (1+
) = 2 = (1+1) = 2
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
= (k+1) ……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
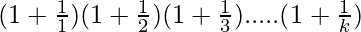
= (
)
De la ecuación (1), obtenemos
= (k+1) (1+
)
= (k+1)
= {(k+1)+1}
Por eso,
P(k+1) = {(k+1)+1}
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 15: 1 2 + 3 2 + 5 2 + …… + (2n-1) 2 = 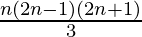
Solución:
Tenemos,
P(n) = 1 2 + 3 2 + 5 2 + …… + (2n-1) 2 =
Para n=1 , obtenemos
P(1) = 1 2 = 1 =
= 1
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1 2 + 3 2 + 5 2 + …… + (2k-1) 2 =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1 2 + 3 2 + 5 2 + …… + (2k-1) 2 + (2(k+1)-1) 2
= (1 2 + 3 2 + 5 2 + …… + (2k-1) 2 ) + (2k+1) 2
De la ecuación (1), obtenemos
=
+ (2k+1) 2
= (2k+1)
= (2k+1)
= (2k+1)
= (2k+1)
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 16: 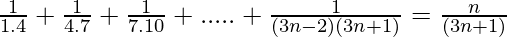
Solución:
Tenemos,
P(n) =
Para n=1 , obtenemos
P(1) =
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
= (
)
De la ecuación (1), obtenemos
=
=
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 17: 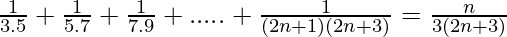
Solución:
Tenemos,
P(n) =
Para n=1 , obtenemos
P(1) =
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) =
……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) =
= (
)
De la ecuación (1), obtenemos
=
=
=
=
=
=
=
Por eso,
P(k+1) =
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 18: 1 + 2 + 3 + ….. + n < 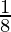 (2n+1) 2
(2n+1) 2
Solución:
Tenemos,
P(n) = 1 + 2 + 3 + ….. + n <
(2n+1) 2
Para n=1 , obtenemos
P(1) = 1 <
(2(1)+1) 2
1 <
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = 1 + 2 + 3 + ….. + k <
(2k+1) 2 ……………..(1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = 1 + 2 + 3 + ….. + k + (k+1)
= (1 + 2 + 3 + ….. + k) + k+1 <
(2k+1) 2 + (k+1)
<
((2k+1) 2 + 8(k+1))
<
((4k 2 +4k+1) + 8k+8))
<
(4k 2 +12k+9)
<
(2k+3) 2
P(k+1) <
(2(k+1)+1) 2
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 19: n (n + 1) (n + 5) es múltiplo de 3.
Solución:
Tenemos,
P (n) = n (n + 1) (n + 5), que es múltiplo de 3
Para n=1 , obtenemos
p(1) = 1 (1 + 1) (1 + 5) = 12, que es múltiplo de 3
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
P(k) = k (k + 1) (k + 5) es múltiplo de 3
P(k) = k (k + 1) (k + 5) = 3m, donde m ∈ N ………… (1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k+1) = (k + 1) {(k + 1) + 1} {(k + 1) + 5}
= (k + 1) (k + 2) {(k + 5) + 1}
Multiplicando los términos
= (k + 1) (k + 2) (k + 5) + (k + 1) (k + 2)
= {k (k + 1) (k + 5) + 2 (k + 1) (k + 5)} + (k + 1) (k + 2)
Usando la ecuación (1), obtenemos
= 3m + (k + 1) {2 (k + 5) + (k + 2)}
= 3m + (k + 1) {2k + 10 + k + 2}
= 3m + (k + 1) (3k + 12)
= 3m + 3 (k + 1) (k + 4)
= 3 {m + (k + 1) (k + 4)}
= 3 × q (donde q = {m + (k + 1) (k + 4)} es un número natural)
(k + 1) {(k + 1) + 1} {(k + 1) + 5} es múltiplo de 3
Por tanto, P(k + 1) es verdadera, siempre que P(k) sea verdadera.
Por tanto, a partir del principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales n.
Pregunta 20: 10 2n – 1 + 1 es divisible por 11.
Solución:
Tenemos,
P (n): 10 2n – 1 + 1 es divisible por 11
Para n=1 , obtenemos
P (1) = 10 2.1 – 1 + 1 = 11, que es divisible por 11
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
10 2k – 1 + 1 es divisible por 11
10 2k – 1 + 1 = 11m, donde m ∈ N …………… (1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
P(k + 1) = 10 2(k + 1) – 1 + 1
= 10 2k + 2 – 1 + 1
= 10 2k + 1 + 1
= 10 2 (10 2k-1 + 1 – 1) + 1
= 10 2 (10 2k-1 + 1) – 10 2 + 1
Usando la ecuación (1), obtenemos
= 10 2 . 11m – 100 + 1
= 100 × 11m – 99
Sacando los términos comunes
= 11 (100m – 9)
= 11r, donde r = (100m – 9) es un número natural
10 2 (k + 1) – 1 + 1 es divisible por 11
P (k + 1) es verdadero siempre que P (k) sea verdadero.
Por lo tanto, por el principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales ien
Pregunta 21: x 2n – y 2n es divisible por x + y.
Solución:
Tenemos,
P (n) = x 2n – y 2n es divisible por x + y
Para n=1 , obtenemos
P (1) = x 2 × 1 – y 2 × 1 = x 2 – y 2 = (x + y) (x – y), que es divisible por (x + y)
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
x 2k – y 2k es divisible por x + y
x 2k – y 2k = m (x + y), donde m ∈ N …… (1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
x2 (k + 1) – y2 (k + 1)
= x 2k . x 2 – y 2k . 2 años
Sumando y restando y 2k obtenemos
= x 2 (x 2k – y 2k + y 2k ) – y 2k . 2 años
Usando la ecuación (1), obtenemos
= x 2 {m (x + y) + y 2k } – y 2k . 2 años
= metro (x + y) x 2 + y 2k . x 2 – y 2k . 2 años
Sacando los términos comunes
= metro (x + y) x2 + y2k ( x2 – y2 )
= m (x + y) x 2 + y 2k (x + y) (x – y)
Entonces obtenemos
= (x + y) {mx 2 + y 2k (x – y)}, que es un factor de (x + y)
P (k + 1) es verdadero siempre que P (k) sea verdadero.
Por lo tanto, por el principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales ien
Pregunta 22: 3 2n+2 – 8n – 9 es divisible por 8.
Solución:
Tenemos,
P (n) = 3 2n + 2 – 8n – 9 es divisible por 8
Para n=1 , obtenemos
P (1) = 3 2 × 1 + 2 – 8 × 1 – 9 = 64, que es divisible por 8
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
3 2k + 2 – 8k – 9 es divisible por 8
3 2k + 2 – 8k – 9 = 8m, donde m ∈ N …… (1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
3 2(k + 1) + 2 – 8 (k + 1) – 9
= 3 2k + 2 . 3 2 – 8k – 8 – 9
Sumando y restando 8k y 9 obtenemos
= 3 2 (3 2k + 2 – 8k – 9 + 8k + 9) – 8k – 17
= 3 2 (3 2k + 2 – 8k – 9) + 3 2 (8k + 9) – 8k – 17
Usando la ecuación (1), obtenemos
= 9. 8m + 9 (8k + 9) – 8k – 17
= 9. 8m + 72k + 81 – 8k – 17
= 9. 8m + 64k + 64
Eliminando los términos comunes
= 8 (9m + 8k + 8)
= 8r, donde r = (9m + 8k + 8) es un número natural
Entonces 3 2(k + 1) + 2 – 8 (k + 1) – 9 es divisible por 8
P (k + 1) es verdadero siempre que P (k) sea verdadero.
Por lo tanto, por el principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales ien
Pregunta 23: 41 n – 14 n es múltiplo de 27.
Solución:
Tenemos,
P (n) = 41 n – 14 n es múltiplo de 27
Para n=1 , obtenemos
P (1) = 41 1 – 14 1 = 27, que es un múltiplo de 27
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
41 k – 14 k es múltiplo de 27
41k – 14k = 27m , donde m ∈ N …… (1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
41 mil + 1 – 14 mil + 1
= 41 k . 41 – 14 k . 14
Sumando y restando 14 k obtenemos
= 41 ( 41k – 14k + 14k ) – 14k . 14
= 41 (41 k – 14 k ) + 41. 14 k – 14 k . 14
Usando la ecuación (1), obtenemos
= 41. 27m + 14k ( 41 – 14)
= 41,27m + 27,14k
Eliminando los términos comunes
= 27 (41m – 14k)
= 27r, donde r = (41m – 14 k ) es un número natural
Entonces 41 k + 1 – 14 k + 1 es un múltiplo de 27
P (k + 1) es verdadero siempre que P (k) sea verdadero.
Por lo tanto, por el principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales ien
Pregunta 24: (2n + 7) < (n + 3) 2 .
Solución:
Tenemos,
P(n) = (2n +7) < (n + 3) 2
Para n=1 , obtenemos
2.1 + 7 = 9 < (1 + 3) 2 = 16
Entonces, P(1) es verdadero
Suponga que P(k) es cierto para algún entero positivo n=k
(2k + 7) < (k + 3) 2 … (1)
Probemos que P(k + 1) también es cierto. Ahora tenemos
{2 (k + 1) + 7} = (2k + 7) + 2
= {2 (k + 1) + 7}
Usando la ecuación (1), obtenemos
(2k + 7) + 2 < (k + 3) 2 + 2
2 (k + 1) + 7 < k 2 + 6k + 9 + 2
2 (k + 1) + 7 < k 2 + 6k + 11
Aquí,
k2 + 6k + 11 < k2 + 8k + 16
2 (k + 1) + 7 < (k + 4) 2
2 (k + 1) + 7 < {(k + 1) + 3} 2
P (k + 1) es verdadero siempre que P (k) sea verdadero.
Por lo tanto, por el principio de inducción matemática, el enunciado P(n) es verdadero para todos los números naturales ien