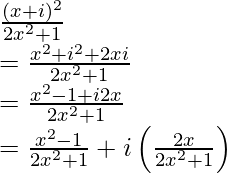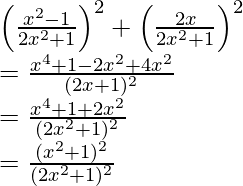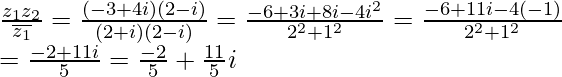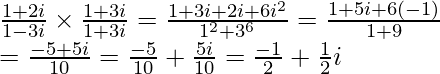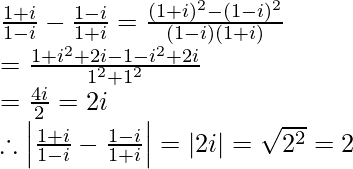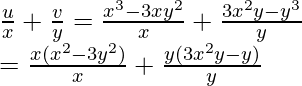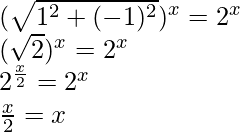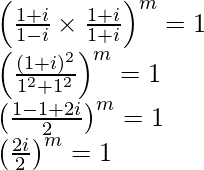Clase 11 Soluciones NCERT – Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio misceláneo en el Capítulo 5

Pregunta 11. Si a + ib = 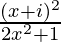$\frac{(x+i)^2}{2x^2+1}$ , demuestre que a ² + b ² =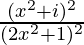 $\frac{(x^2+i)^2}{(2x^2+1)^2}$

Solución:

Dado:

a + ib = $\frac{(x+i)^2}{2x^2+1}\\ =\frac{x^2+i^2+2xi}{2x^2+1}\\ =\frac{x^2-1+i2x}{2x^2+1}\\ =\frac{x^2-1}{2x^2+1}+i\left(\frac{2x}{2x^2+1}\right)$

Al comparar las partes real e imaginaria, tenemos

a = $\frac{(x-1)}{2x^2+1}$ y b = $\frac{2x}{2x^2+1}$

Por lo tanto,

un ² + ^{segundo 2} = $\left(\frac{x^2-1}{2x^2+1}\right)^2+\left(\frac{2x}{2x^2+1}\right)^2\\ =\frac{x^4+1-2x^2+4x^2}{(2x+1)^2}\\ =\frac{x^4+1+2x^2}{(2x^2+1)^2}\\ =\frac{(x^2+1)^2}{(2x^2+1)^2}$

Por lo tanto, probado,

un ² + ^{segundo 2} = $\frac{(x^2+1)^2}{(2x^2+1)^2}$

Pregunta 12. Sea z ₁ = 2 – i , z ₂ = -2 + i . Encontrar

(i) $Re\left(\frac{z_1z_2}{\overline{z_1}}\right)$

(ii) $Im\left(\frac{1}{z_1\overline{z_2}}\right)$

Solución:

(i) Dado:

z ₁ = 2 – yo, z ₂ = -2 + yo

(i) z ₁ z ₂ = (2 – i)(-2 + i) = -4 + 2i + 2i – i ² = -4 + 4i – (-1) = -3 + 4i

$\overline{z_1}$ = 2 + yo

Por lo tanto,

$\frac{z_1z_2}{\overline{z_1}}=\frac{-3+4i}{2+i}$

Al multiplicar numerador y denominador por (2 – i), obtenemos

$\frac{z_1z_2}{\overline{z_1}}=\frac{(-3+4i)(2-i)}{(2+i)(2-i)}=\frac{-6+3i+8i-4i^2}{2^2+1^2}=\frac{-6+11i-4(-1)}{2^2+1^2}\\ =\frac{-2+11i}{5}=\frac{-2}{5}+\frac{11}{5}i$

Al comparar las partes reales, tenemos

$Re\left(\frac{z_1z_2}{\overline{z_1}}\right)=\frac{-2}{5}$

(ii) $\frac{1}{z_1\overline{z_2}}=\frac{1}{(2-1)(2+i)}=\frac{1}{(2)^2+(1)^2}=\frac{1}{5}\\$

Al comparar la parte imaginaria, obtenemos

$Im\left(\frac{1}{z_1\overline{z_2}}\right)$ = 0

Pregunta 13. Encuentra el módulo y el argumento del número complejo 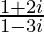$\frac{1+2i}{1-3i}$

Solución:

Sea, z = $\frac{1+2i}{1-3i}$ , entonces

z = $\frac{1+2i}{1-3i}\times\frac{1+3i}{1+3i}=\frac{1+3i+2i+6i^2}{1^2+3^6}=\frac{1+5i+6(-1)}{1+9}\\ =\frac{-5+5i}{10}=\frac{-5}{10}+\frac{5i}{10}=\frac{-1}{2}+\frac{1}{2}i$

Sea z = r cosθ + ir senθ

Asi que,

r cosθ = $\frac{-1}{2}$ y r sinθ = $\frac{1}{2}$

Al elevar al cuadrado y sumar, obtenemos

r2(cos2θ + sen2θ) = $\left(\frac{-1}{2}\right)^2+\left(\frac{1}{2}\right)^2$

r2 = ^_ $\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\ \ \ \ \ \ [Conventionally,\ r>0]$

r = $\frac{1}{\sqrt2}$

Ahora,

$\frac{1}{\sqrt2}$ cosθ = $\frac{-1}{2}$ y $\frac{1}{\sqrt2}$ senθ = $\frac{1}{2}$

= cosθ = $\frac{-1}{\sqrt2}$ y senθ = $\frac{1}{\sqrt2}$

Por lo tanto,

θ = $\pi-\frac{\pi}{4}=\frac{3\pi}{4}$ [Como θ se encuentra en el cuadrante II]

Pregunta 14. Encuentra los números reales x e y si ( x – iy ) (3 + 5 i ) es el conjugado de – 6 – 24 i .

Solución:

Supongamos z = ( x – iy ) (3 + 5 i )

z = 3x + xi – 3yi – 5yi ² = 3x + 5xi – 3yi + 5y = (3x + 5y) + i(5x – 3y)

Por lo tanto,

$\overline{z}$ =(3x + 5y) – i(5x – 3y)

También dado, $\overline{z}$ = -6 – 24i

Y,

(3x + 5y) – i (5x – 3y) = -6 -24 i

Después de igualar las partes real e imaginaria, obtenemos

3x + 5y = -6 …… (yo)

5x – 3y = 24 …… (ii)

Después de hacer (i) x 3 + (ii) x 5, tenemos

(9x + 15y) + (25x – 15y) = -18 + 120

34x = 102

x = 102/34 = 3

Poniendo el valor de x en la ecuación (i), obtenemos

3(3) + 5y = -6

5 años = -6 – 9 = -15

y = -3

Por lo tanto, los valores de x e y son 3 y –3 respectivamente.

Pregunta 15. Encuentra el módulo de 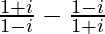$\frac{1+i}{1-i}-\frac{1-i}{1+i}$

Solución:

$\frac{1+i}{1-i}-\frac{1-i}{1+i}=\frac{(1+i)^2-(1-i)^2}{(1-i)(1+i)}\\ =\frac{1+i^2+2i-1-i^2+2i}{1^2+1^2}\\ =\frac{4i}{2}=2i\\ \therefore\left|\frac{1+i}{1-i}-\frac{1-i}{1+i}\right|=|2i|=\sqrt{2^2}=2$

Pregunta 16. Si ( x + iy ) ³ = u + iv , entonces demuestre que 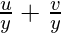$\frac{u}{y}+\frac{v}{y}$ = 4(x ² – y ² )

Solución:

(x + iy) ³ = u + iv

x ³ + (iy) ³ + 3 × x × iy(x + iy) = u + iv

x ³ + yo ³ y ³ + 3x ² yi + 3xy ² = tu + iv

x ³ – iy ³ + 3x ² yi – 3xy ² = u + iv

(x ³ – 3xy ² ) + i(3x ² y – y ³ ) = u + iv

Al igualar las partes real e imaginaria, obtenemos

u = x ³ – 3xy ² , v = 3x ² y – y ³

$\frac{u}{x}+\frac{v}{y}=\frac{x^3-3xy^2}{x}+\frac{3x^2y-y^3}{y}\\ =\frac{x(x^2-3y^2)}{x}+\frac{y(3x^2y-y)}{y}$

= x ² – 3y ² + 3x ² – y ²

= 4x ² – 4y ²

= 4( ^x2 – ^y2 )

$\therefore\frac{u}{x}+\frac{v}{y}=4(x^2-y^2)$

Por lo tanto probado

Pregunta 17. Si α y β son números complejos diferentes con |β| = 1, luego encuentra $\left|\frac{\beta-\alpha}{1-\overline{\alpha}\beta}\right|$

Solución:

Suponga que α = a + ib y β = x + iy

Dado: |β| = 1

Asi que, $\sqrt{x^2+y^2}=1$

= x2 + y2 = 1 ….(1)

$\left|\frac{\beta-\alpha}{1-\overline{\alpha}\beta}\right|=\left|\frac{(x+iy)(a+ib)}{1-(a-ib)(x+iy)}\right|\\ =\left|\frac{(x-a)+i(y-b)}{1-(ax+aiy-ibx+by)}\right|\\ =\left|\frac{(x-a)+i(y-b)}{(1-ax-by)+i(bx-ay)}\right|\\ =\left|\frac{(x-a)+i(y-b)}{(1-ax-by)+i(bx-ay)}\right|\ \ \ \ \ \left[\left|\frac{z_1}{z_2}\right|=\left|\frac{z_1}{z_2}\right|\right]\\ =\frac{\sqrt{(x-a)^2+(y-b)^2}}{\sqrt{(1-ax-by)^2+(bx-ay)^2}}\\ =\frac{\sqrt{x^2+a^2-2ax+y^2+b^2-2by}}{\sqrt{1+a^2x^2+b^2y^2-2ax+2abxy-2by+b^2x^2+a^2y^2-2abxy}}\\ =\frac{\sqrt{(x^2+y^2)+a^2+b^2-2ax-2by}}{\sqrt{1+a^2(x^2+y^2)+b^2(y^2+x^2)-2ax-2by}}\\ =\frac{\sqrt{1+a^2+b^2-2ax-2by}}{\sqrt{1+a^2+b^2-2ax-2by}}\ \ \ \ \ \ \ \ [Using\ (1)]$

= 1

$\therefore\left|\frac{\beta-\alpha}{1-\overline{\alpha}\beta}\right|=1$

Pregunta 18. Encuentra el número de soluciones integrales distintas de cero de la ecuación |1 – i| ^x = 2 ^x

Solución:

|1 – yo| ^x = 2 ^t

$(\sqrt{1^2+(-1)^2})^x=2^x\\ (\sqrt2)^x=2^x\\ 2^{\frac{x}{2}}=2^x\\ \frac{x}{2}=x$

x = 2x

2x – x = 0

Por lo tanto, ‘0’ es la única solución integral de la ecuación dada.

Por lo tanto, el número de soluciones integrales distintas de cero de la ecuación dada es 0.

Pregunta 19. Si (a + ib) (c + id) (e + if) (g + ih) = A + iB, entonces demuestre que (a ² + b ² ) (c ² + d ² ) (e ² + F ² ) ( gramo ² + h ² ) = UN ² + ^{segundo 2} .

Solución:

Dado:

(a + ib)(c + id)(e + si)(g + ih) = A + iB

Por lo tanto,

|(a + ib)(c + id)(e + si)(g + ih)| = |A + iB|

= |(a + ib)| × |(c + identificación)| × |(e + si)| × |(g + h)| = |A + iB|

$\sqrt{a^2+b^2}\times\sqrt{c^2+d^2}\times\sqrt{e^2+f^2}\times\sqrt{g^2+h^2}=\sqrt{A^2+B^2}$

Al elevar al cuadrado ambos lados, obtenemos

( un ² + segundo ² ) ( do ² + re ² ) ( mi ² + f ²) ( gramo ² + h ² ) = UN ² + ^{segundo 2}

Por lo tanto, probado.

Pregunta 20. Si, entonces encuentre el valor integral mínimo positivo de m. $\left(\frac{1+i}{1-i}\right)^m=1$

Solución:

$\left(\frac{1+i}{1-i}\right)^m=1$

$\left(\frac{1+i}{1-i}\times\frac{1+i}{1+i}\right)^m=1\\ \left(\frac{(1+i)^2}{1^2+1^2}\right)^m=1\\ \left(\frac{1-1+2i}{2}\right)^m=1\\ \left(\frac{2i}{2}\right)^m=1$

yo ^m = 1

Por lo tanto, m = 4k, donde k es un número entero.

Por lo tanto, el menor entero positivo es 1.

Por tanto, el menor valor integral positivo de m es 4 (= 4 × 1).

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones NCERT – Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio misceláneo en el Capítulo 5 | conjunto 2

Pregunta 11. Si a + ib = $\frac{(x+i)^2}{2x^2+1}$ , demuestre que a ² + b ² = $\frac{(x^2+i)^2}{(2x^2+1)^2}$

Pregunta 12. Sea z ₁ = 2 – i , z ₂ = -2 + i . Encontrar

Pregunta 13. Encuentra el módulo y el argumento del número complejo $\frac{1+2i}{1-3i}$

Pregunta 14. Encuentra los números reales x e y si ( x – iy ) (3 + 5 i ) es el conjugado de – 6 – 24 i .

Pregunta 15. Encuentra el módulo de $\frac{1+i}{1-i}-\frac{1-i}{1+i}$

Pregunta 16. Si ( x + iy ) ³ = u + iv , entonces demuestre que $\frac{u}{y}+\frac{v}{y}$ = 4(x ² – y ² )

Pregunta 17. Si α y β son números complejos diferentes con |β| = 1, luego encuentra $\left|\frac{\beta-\alpha}{1-\overline{\alpha}\beta}\right|$

Pregunta 18. Encuentra el número de soluciones integrales distintas de cero de la ecuación |1 – i| ^x = 2 ^x

Pregunta 19. Si (a + ib) (c + id) (e + if) (g + ih) = A + iB, entonces demuestre que (a ² + b ² ) (c ² + d ² ) (e ² + F ² ) ( gramo ² + h ² ) = UN ² + ^{segundo 2} .

Pregunta 20. Si, entonces encuentre el valor integral mínimo positivo de m. $\left(\frac{1+i}{1-i}\right)^m=1$

Deja una respuesta Cancelar la respuesta

Pregunta 11. Si a + ib = , demuestre que a 2 + b 2 =

Pregunta 12. Sea z 1 = 2 – i , z 2 = -2 + i . Encontrar

Pregunta 13. Encuentra el módulo y el argumento del número complejo

Pregunta 14. Encuentra los números reales x e y si ( x – iy ) (3 + 5 i ) es el conjugado de – 6 – 24 i .

Pregunta 15. Encuentra el módulo de

Pregunta 16. Si ( x + iy ) 3 = u + iv , entonces demuestre que = 4(x 2 – y 2 )

Pregunta 17. Si α y β son números complejos diferentes con |β| = 1, luego encuentra

Pregunta 18. Encuentra el número de soluciones integrales distintas de cero de la ecuación |1 – i| x = 2 x

Pregunta 19. Si (a + ib) (c + id) (e + if) (g + ih) = A + iB, entonces demuestre que (a 2 + b 2 ) (c 2 + d 2 ) (e 2 + F 2 ) ( gramo 2 + h 2 ) = UN 2 + segundo 2 .

Pregunta 20. Si, entonces encuentre el valor integral mínimo positivo de m.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Si a + ib = $\frac{(x+i)^2}{2x^2+1}$ , demuestre que a ² + b ² = $\frac{(x^2+i)^2}{(2x^2+1)^2}$

Pregunta 12. Sea z ₁ = 2 – i , z ₂ = -2 + i . Encontrar

Pregunta 13. Encuentra el módulo y el argumento del número complejo $\frac{1+2i}{1-3i}$

Pregunta 15. Encuentra el módulo de $\frac{1+i}{1-i}-\frac{1-i}{1+i}$

Pregunta 16. Si ( x + iy ) ³ = u + iv , entonces demuestre que $\frac{u}{y}+\frac{v}{y}$ = 4(x ² – y ² )

Pregunta 17. Si α y β son números complejos diferentes con |β| = 1, luego encuentra $\left|\frac{\beta-\alpha}{1-\overline{\alpha}\beta}\right|$

Pregunta 18. Encuentra el número de soluciones integrales distintas de cero de la ecuación |1 – i| ^x = 2 ^x

Pregunta 19. Si (a + ib) (c + id) (e + if) (g + ih) = A + iB, entonces demuestre que (a ² + b ² ) (c ² + d ² ) (e ² + F ² ) ( gramo ² + h ² ) = UN ² + ^{segundo 2} .

Pregunta 20. Si, entonces encuentre el valor integral mínimo positivo de m. $\left(\frac{1+i}{1-i}\right)^m=1$