Pregunta 1. Evaluar ![Rendered by QuickLaTeX.com \left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9204b8902fbce319746190720a4ed916_l3.png)
Solución:
= [-1 – yo] 3
= (-1) 3 [1 + yo] 3
= -[1 3 + yo 3 + 3 × 1 × yo (1 + yo)]
= -[1 + i 3 + 3i + 3i 2 ]
= -[1 – yo + 3i – 3]
= -[2 + 2i]
= 2 – 2i
Pregunta 2. Para cualesquiera dos números complejos z 1 y z 2 , demuestre que, Re (z 1 z 2 ) = Re z 1 Re z 2 – Im z 1 Im z 2
Solución:
Supongamos que z 1 = x 1 + iy 1 y z 2 = x 2 + iy 2 como dos números complejos
Producto de estos números complejos, z 1 z 2
z 1 z 2 = (x 1 + iy 1 )(x 2 + iy 2 )
= x 1 (x 2 + iy 2 ) + iy 1 (x 2 + iy 2 )
= x 1 x 2 + ix 1 y 2 + iy 1 x 2 + yo 2 y 1 y 2
= x 1 x 2 + ix 1 y 2 + iy 1 x 2 – y 1 y 2 [i 2 = -1]
= (x 1 x 2 – y 1 y 2 ) + i(x 1 y 2 + y 1 x 2 )
Ahora,
Re(z 1 z 2 ) = x 1 x 2 – y 1 y 2
⇒ Re(z 1 z 2 ) = Rez 1 Rez 2 – Imz 1 Imz 2
Por lo tanto, probado.
Pregunta 3. Reducir a la forma estándar 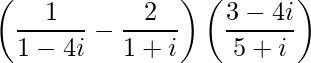
Solución:
Sobre multiplicar numerador y denominador por (14+5i)
Por lo tanto, esta es la forma estándar requerida.
Pregunta 4. Si x – iy = 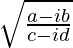 prueba que (x 2 + y 2 ) 2
prueba que (x 2 + y 2 ) 2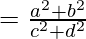
Solución:
Dado:
x-iy =
Al multiplicar numerador y denominador por (c+id)
Asi que,
(x – iy) 2 =
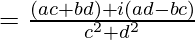
x 2 – y 2 – 2ixy
Al comparar las partes real e imaginaria, obtenemos
x2 – y2 = ,
-2xy =
(1)
(x 2 + y 2 ) 2 = (x 2 – y 2 ) 2 + 4x 2 y 2
=
Por lo tanto probado
Pregunta 5. Convierta lo siguiente en la forma polar:
(i) ![]()
(ii) ![]()
Solución:
(i) Aquí, z =
=
Multiplicando por su conjugado en el numerador y denominador
= -1+yo
Sea r cos θ = -1 y r sen θ = 1
Al elevar al cuadrado y sumar, obtenemos
r 2 (cos 2 θ + sen 2 θ) = 1 + 1 = 2
r 2 = 2 [cos 2 θ + sen 2 θ = 1]
r = √2
Asi que,
√2 cosθ = -1 y √2 senθ = 1
⇒ cosθ =
y senθ =
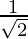
Por lo tanto,
θ =
[Como θ se encuentra en el II cuadrante]
Expresando como, z = r cos θ + ir sen θ
=
Por lo tanto, esta es la forma polar requerida.
(ii) Sea, z =
= -1 + yo
Ahora, sea r cosθ = -1 y r sin θ = 1
Al elevar al cuadrado y sumar, obtenemos
r 2 (cos 2 θ + sen 2 θ) = 1 + 1
r(cos 2 θ + sen 2 θ) = 2
r 2 = 2 [cos2θ + sen2θ = 1]
= r = √2 [Convencionalmente, r > 0]
Por lo tanto,
√2 cosθ = -1 y √2 senθ = 1
cosθ =
y senθ =
Por lo tanto,
θ =
[Como θ se encuentra en el II cuadrante]
Expresando como, z = r cosθ + ir sinθ
z =
Por lo tanto, esta es la forma polar requerida.
Resuelva cada una de las ecuaciones de los ejercicios 6 a 9.
Pregunta 6. 3x 2 – 4x + 20/3 = 0
Solución:
Dada la ecuación cuadrática, 3x 2 – 4x + 20/3 = 0
Se puede reescribir como: 9x 2 – 12x + 20 = 0
Al compararlo con ax 2 + bx + c = 0, obtenemos
a = 9, b = –12 y c = 20
Entonces, el discriminante de la ecuación dada será
D = segundo 2 – 4 ca = (–12) 2 – 4 × 9 × 20 = 144 – 720 = –576
Por lo tanto, las soluciones requeridas son
X =
Pregunta 7. x 2 – 2x + 3/2 = 0
Solución:
Dado:
Ecuación cuadrática, x 2 – 2x +
= 0
Después de reescribir 2x 2 – 4x + 3 = 0
Al compararlo con ax 2 + bx + c = 0,
Obtenemos
a = 2, b = –4 y c = 3
Entonces, el discriminante de la ecuación dada será
re = segundo 2 – 4 ac = (–4) 2 – 4 × 2 × 3 = 16 – 24 = –8
Por lo tanto, las soluciones requeridas son
x =
Pregunta 8. 27x 2 – 10x + 1 = 0
Solución:
Dado:
Ecuación cuadrática, 27 x 2 – 10 x + 1 = 0
Al compararlo con ax 2 + bx + c = 0,
Obtenemos
a = 27, b = –10 y c = 1
Entonces, el discriminante de la ecuación dada será
re = segundo 2 – 4 ac = (–10) 2 – 4 × 27 × 1 = 100 – 108 = –8
Por lo tanto, las soluciones requeridas son
Pregunta 9. 21x 2 – 28x + 10 = 0
Solución:
Dado:
Ecuación cuadrática, 21 x 2 – 28 x + 10 = 0
Al compararlo con ax 2 + bx + c = 0,
Tenemos
a = 21, b = –28 y c = 10
Entonces, el discriminante de la ecuación dada será
D = segundo 2 – 4 ca = (–28) 2 – 4 × 21 × 10 = 784 – 840 = –56
Por lo tanto, las soluciones requeridas son
Pregunta 10. Si z 1 = 2 – i , z 2 = 1 + i , encuentra 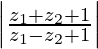
Solución:
Dado, z 1 = 2 – i , z 2 = 1 + i
Por lo tanto, el valor de
es √2
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \displaystyle\left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^3\\ =\left[i^{4\times4+2}+\frac{1}{i^{4\times6+1}}\right]^3\\ =\left[(i^4)^{4}.i^2+\frac{1}{(i^4)^6.i}\right]^3\\ =\left[i^2+\frac{1}{i}\right]^3\ \ \ \ \ \ [i^4=1]\\ =\left[-1+\frac{1}{i}\times\frac{i}{i}\right]^3\ \ \ \ \ \ [i^2=-1]\\ =\left[-1+\frac{i}{i^2}\right]^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-de17eb3266c9f824364c873e58d1b97b_l3.png)
![Procesado por QuickLaTeX.com \displaystyle\left(\frac{1}{1-4i}-\frac{2}{1+i}\right)\left(\frac{3-4i}{5+i}\right)=\left[\frac{(1+i)-2(1-4i)}{(1-4i)(1+i)}\right]\left[\frac{3-4i}{5+i}\right]\\ = \left[\frac{1+i-2+8i}{1+i-4i-4i^2}\right] \left[\frac{3-4i}{5+i}\right]= \left[\frac{-1+9i}{5-3i}\right] \left[\frac{3-4i}{5+i}\right]\\ = \left[\frac{-3+4i+27i-36i^2}{25+5i-15i-3i^2}\right]=\frac{33+31i}{28-10i}=\frac{33+31i}{2(14-5i)}\\ = \frac{(33+31i)}{2(14-5i)}\times\frac{14+5i}{14+5i}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c15226e112c8e1996a8c7eea62f4e566_l3.png)
![Rendered by QuickLaTeX.com \\ =\frac{462+165i+434i+155i^2}{2[(14)^2-(5i)^2]}=\frac{307+599i}{2(196-25i^2)}\\ =\frac{307+599i}{2(221)}=\frac{307+599i}{442}=\frac{307}{442}+\frac{599i}{442}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b76cc1fad43040e25508228c57b7cdf9_l3.png)

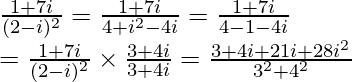


![Rendered by QuickLaTeX.com \frac{-b\pm\sqrt{D}}{2a}=\frac{-(-4)\pm\sqrt{-8}}{2\times2}=\frac{4\pm2\sqrt2i}{4}\ \ \ \ [\sqrt{-1}=i]\\ =\frac{2\pm\sqrt2i}{2}=1\pm\frac{\sqrt2}{2}i](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-891d07c7751cd344a36d72a9695b3a00_l3.png)

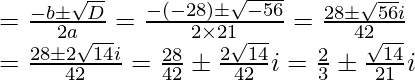
![Rendered by QuickLaTeX.com \left|\frac{z_1+z_2+1}{z_1-z_2+1}\right|=\left|\frac{(2-i)+(1+i)+1}{(2-i)-(1+i)+1}\right|\\ =\left|\frac{4}{2-2i}\right|=\left|\frac{4}{2(1-i)}\right|\\ =\left|\frac{2}{1-i}\times\frac{1+i}{1+i}\right|=\left|\frac{2(1+i)}{1^2-i^2}\right|\\ =\left|\frac{2(1+i)}{1+1}\right|\ \ \ \ \ [i^2=-1]\\ =\left|\frac{2(1+i)}{2}\right|\\ =|1+i|=\sqrt{1^2+1^2}=\sqrt2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c409c10a79cb7ac251f186e0fffa7aa_l3.png)